
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость системы лду. Необходимое и достаточное условие устойчивости линейной системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
A(t)=|| В этом случае задача Коши имеет единственное решение, определенный на [
Теорема 1. Решение задачи Коши (3), Док-во: обозначим:
=A(t)[
33.Следствие 1. Все решения системы ЛДУ устойчивы (ассимтотически устойчивы), если у этой системы Следствие 3. Система ЛДУ называется (асимтотически) устойчивой, если у нее
Замечание. 1) вектор-функция 2)
3)Если Теорема 2. Система ЛДУ устойчива т и тт, когда все решения этой системы ограниченны (без док-ва) 37. Исследование устойчивости положения покоя системы двух ЛДУ с постоянными коэффициентами в случае
Точки покоя:
det(A-λE) = 0
1)
Решение периодично T= x(t)=x(t+T)
Все фазовые траектории замкнуты Центр (нет асимптотической устойчивости)
Система асимптотически устойчива; фазовые траектории: спирали, накрученные на точку покоя
Устойчивый фокус
а)
спирали
Неустойчивый фокус
38. Исследование устойчивости положения покоя системы двух ЛДУ с постоянными коэффициентами в случае
Точки покоя:
det(A-λE) = 0
1) Матрица А имеет 1 линейно независимый собственный вектор (к
а) асимптоти-чески устойчивая система
Устойчивый вырожденный узел б)
2) Матрица А имеет 2 линейно независимых собственных вектора
a) асимптотически устойчивая система
б) Неустойчивый дикритический узел
39. Исследование устойчивости положения покоя системы двух ЛДУ с постоянными коэффициентами в случае
Точки покоя:
det(A-λE) = 0
Точек покоя бесконечное множество
Все точки покоя заполняют прямую
а) Нелинейные системы. Исследование устойчивости по первому приближению. Теорема Ляпунова. dx/dt=f(t,x);(9) dxi/dt=fi(t,x1…xn); f(t, пусть система (9) предст. в виде dx/dt=A(t)x+R(t,x) (10) где А(t)=a ij (t), где a ij (t)
Тогда dx/dt=A(t)x называется системой первого приближения для (9),(10). Теорема Ляпунова: пусть вектор-функция R(t,x) непрерывно диффер. при а А(t) имеют отриц. действит. корни, то нулевое решение системы (9) и (10) асимптот. устойчивое. 2)если сущ. Корень характер. уравнения, имеющий положит.действит. числа, то нулевое решение системы неустойчиво. (БЕЗ ДОКАЗАТЕЛЬСТВА) Теорема. Если вектор-функция f(x) дважды непрерывно диффер. В окрестности точки х=0 и f(0)=0, то система dx/dt=f(x) приводится к виду dx/dt=A(t)x+R(t,x) и для нее справедливы условия теоремы Ляпунова.
Понятие фазового пространства и фазовой траектории. Автономные системы ОДУ, св-ва их фазовых траекторий.
Считается, что Пусть Кривая Г: -интегральная кривая системы (6) Гс Определение. Пространство Определение. Если функции То система ОДУ называется автономной Определение. Точка
|
|||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.136 (0.009 с.) |

 (3)
(3) 
 (t)|
(t)|  C[
C[ 



 устойчиво (ассимтотически устойчиво), если нулевое решение приведенной однородной системы ЛДУ:
устойчиво (ассимтотически устойчиво), если нулевое решение приведенной однородной системы ЛДУ: 
 где
где 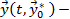 решение (3),
решение (3),  [А(t)
[А(t)  +
+  -[A(t)
-[A(t)  =
= =
= 


 хотя бы одно (асимтотически) устойчивое решение.
хотя бы одно (асимтотически) устойчивое решение. =
=  - устойчиво, если
- устойчиво, если 
 назывется ограниченной на множестве
назывется ограниченной на множестве  , если
, если  такое, что
такое, что 
 =
= 
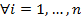 ограниченна на
ограниченна на 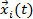
 ||
||  , то
, то  i=1,…,n
i=1,…,n  ||
||  M
M ,
,  - комплексные.
- комплексные. A=
A=  ,
, ;
; 

 ,
, 
 , единственная точка покоя (0,0).
, единственная точка покоя (0,0). =0 – характеристическое уравнение.
=0 – характеристическое уравнение. – корни характеристического уравнения.
– корни характеристического уравнения.




 =0,
=0,  ,
,  ,
, 

 , т.е. нулевое реш. не явл. асимптотически уст.
, т.е. нулевое реш. не явл. асимптотически уст.
 y(t)=y(t+T)
y(t)=y(t+T) а)
а)  =Re
=Re  ,
,  ,
,
 ,
, Система неустойчива; фазовые траектории: раскрученные
Система неустойчива; фазовые траектории: раскрученные

 кратные корни
кратные корни =
=  +
+ 
 -собственный вектор, отвечающий
-собственный вектор, отвечающий 
 )
)

 неустойчивая система
неустойчивая система Неустойчивый вырожденный узел
Неустойчивый вырожденный узел ,
, 
 +
+  =
= 

 ,
,  y=
y=  x
x ,
, устойчивый дикритический узел
устойчивый дикритический узел .
. =0, пусть
=0, пусть  .
. =0.
=0. 


 .
.  .
. ,
,
 +
+  параметрическое задание прямой с направляющим вектором
параметрическое задание прямой с направляющим вектором 
 )=
)=  [t0;
[t0;  ) выполняется неравенство:
) выполняется неравенство:
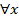 (IIxII<C0) и для
(IIxII<C0) и для  [t0;
[t0;  , тогда 1)если все корни det(A-λE) = 0
, тогда 1)если все корни det(A-λE) = 0 =
=  (6)
(6)  =
=  i=1,…,n
i=1,…,n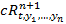
 =
=  (t), t
(t), t  –решение системы (6)
–решение системы (6) –
– – пространство решений
– пространство решений называется фазовым пространством системы (6), а кривая
называется фазовым пространством системы (6), а кривая  , задаваемая направлением
, задаваемая направлением  , где
, где  - решение системы (5), называется фазовой траекторией системы (5).
- решение системы (5), называется фазовой траекторией системы (5). не зависят явно от
не зависят явно от  , т.е. система имеет вид (7)
, т.е. система имеет вид (7)  ;
; 
 =(
=( ,…,
,…,  называется точкой покоя (положением равновесия) автономной системы (7), если
называется точкой покоя (положением равновесия) автономной системы (7), если  , т.е.
, т.е. 



