
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий устойчивости Михайлова.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предложен Михайловым (сов. ученый) в 1936 году. Позволяет судить об устойчивости замкнутой системы по виду кривой Михайлова, представляющей собой годограф вектора
при изменении Годограф представляет собой характеристический полином замкнутой системы D(s) при s=j Выделив в правой части (1) вещественную и мнимую составляющие можно записать D(j
Кривая Михайлова строится в плоскости (U;jV) по точкам в соответствии с (2). Критерий Михайлова формулируется таким образом: Для устойчивости линейной САР необходимо и достаточно, чтобы вектор D(j D(s)=a0(s-s1)(s-s2)..(s-sn) Где s1 s2... sn – корни характеристического уравнения Кривая Михайлова может быть описана уравнением D( Результирующий угол поворота вектора D(j Где ¡ =arctg(b ¤ a) (si=±a ±jb). Паре комплексных корней соответствуют два сомножителя, поворачивающие радиус вектор на угол ±p. Положительные повороты (против часовой стрелки) имеют место при отрицательной вещественной части корня.
При изменении j Таким образом, если характеристическое уравнение замкнутой системы будет иметь l3 корней с положительными вещественными частями, то каковы бы ни были эти корни (вещественные или мнимые), им будет соответствовать сумма углов поворота, равная -l3 ·p/2 Остальным (n-l3) корням, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворота, равная (n- l3) ·p/2. Следовательно, результирующий угол поворота вектора D(j
Критерий Найквиста
Этот критерий позволяет судить об устойчивости САР по виду ее АФХ в разомкнутом состоянии.
Передаточная функция замкнутой САР может быть выражена через передаточную функцию разомкнутой системы W(s). Ф(s)=W(s)/(1+W(s)) Пусть W(s)=M(s)/Q(s), где M(s) и D(s) – многочлены от s, причем степень многочлена M(s) меньше степени многочлена Q(s). Передаточная функция замкнутой системы имеет вид:
где Многочлен D(s) является характеристическим многочленом замкнутой, а многочлен Q(s) – разомкнутой автоматической системы. Очевидно, что степени этих многочленов равны. Образуем сумму W1(j Из критерия Михайлова следует, что замкнутая система будет устойчивой, если приращение аргумента Yd=n·p/2, где n -степень характеристического многочлена D(s); при этом условии D(s) не имеет корней в правой полуплоскости плоскости S. В разомкнутом состоянии САР в общем случае может быть неустойчивой, то есть Q(s) может иметь корни в правой полуплоскости (полагаем, что на мнимой оси Q(s) корней не имеет). Если число таких корней равно L, то приращение аргумента (угол поворота вектора Q(j от 0 до ¥) Yq=n·p/2-p·L Следовательно, угол поворота вектора суммы W1(j Y=Yd - Yq= n·p/2 - n·p/2-n·L=p L Для устойчивой системы вектор W1(j На основании выше изложенного, критерий Найквиста может быть сформулирован следующим образом:
-1;j0
Автоматическая система, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если АФХ разомкнутой системы W(j Примеры. Разомкнутая система неустойчива
L=1 y=p, охватывает ½ раз - система устойчива П++П-= ½
y=-p¹p, - система не устойчива П++П-=½-1¹½ - не устойчива
L=2 y=2p, охватывает 1 раз L/2 – замкнутая система устойчива
П+-П -= 1 – устойчива. Если АФХ имеет сложную форму, то определение результирующего поворота (охвата) сложно. В этом случае удобно использовать правило переходов. Переход АФХ W(jw) через участок вещественной оси (-¥,-1) с возрастанием частоты называется положительным если он проходит “сверху”-”вниз” и отрицательным, если “снизу”-”вверх”. Обозначают + и – в кружочках. Если АФХ начинается на вещественной оси в интервале (-¥;-1), то эта точка считается за + ½ перехода, если вниз, и за - ½, если вверх. Если разомкнутая система является неустойчивой, то для устойчивости замкнутой системы необходимо и достаточно, чтобы разность между общим числом П+ - положительных и П -- отрицательных переходов АФХ W(j П+ -П - =L/2 Разомкнутая система – устойчива L=0 y=0 П+-П -=0 устойчива замкнутая система
y=0 П+-П-=0 замкнутая система устойчива не охватывает
y=2p;¹0
П+-П-= -1¹0 замкнутая система не устойчива охватывает
Если АФХ проходит через (-1;j0) то замкнутая система находится на колебательной границе устойчивости. Некоторые особенности применения критерия Найквиста появляются при исследовании устойчивости систем, нейтральных в разомкнутом состоянии. Это системы имеющие нулевые корни (апериодическая граница устойчивости), а также системы, находящиеся в разомкнутом состоянии, на колебательной границе устойчивости, то есть имеющих чисто мнимые корни.
В этом случае для сохранения формулировки критерия, справедливой для устойчивых в разомкнутом состоянии систем, включают нулевой корень в левую полуплоскость, огибая его справа окружностью бесконечно малого радиуса r®0. При этом годограф W(j
Аналогичные дополнения приходится проводить при наличии чисто мнимых корней в характеристическом уравнении разомкнутой системы, так как в этом случае АФХ имеют разрывы
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 622; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.127 (0.009 с.) |


 от 0 до ¥.
от 0 до ¥. (2)
(2)
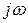 )=a0(j
)=a0(j 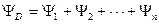 ,
, (i=1..n) – составляющие угла поворота вектора D(j
(i=1..n) – составляющие угла поворота вектора D(j  Действительно, каждому множителю (j
Действительно, каждому множителю (j  Для устойчивой САР кривая Михайлова должна проходить последовательно n квадрантов. Кривая начинается на вещественной полуоси (при
Для устойчивой САР кривая Михайлова должна проходить последовательно n квадрантов. Кривая начинается на вещественной полуоси (при 






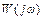








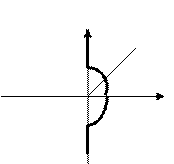 Например, если Q(s) имеет один нулевой корень, то годограф W(j
Например, если Q(s) имеет один нулевой корень, то годограф W(j 

 При нескольких нулевых корнях, угол дополнения АФХ окружностью бесконечно малого радиуса yдоп=¡p/2 где ¡- число нулевых корней (порядок астатизма)
При нескольких нулевых корнях, угол дополнения АФХ окружностью бесконечно малого радиуса yдоп=¡p/2 где ¡- число нулевых корней (порядок астатизма)




