
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение устойчивости системы управления алгебраическим критериемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Содержание 1 Определение весовой функции ω (t)……………………………………………3 2 Определение переходной функции h (t)……………………………………….4 3 Структурные преобразования…………………………………………………5 4 Определение устойчивости системы управления алгебраическим критерием………………………………………………………………………….8 4.1 Определение устойчивости системы управления критерием Гурвица….8 4.2 Определение устойчивости системы управления критерием Рауса……..9 5 Определение устойчивости системы управления частотным критерием….9 5.1 Определение устойчивости системы управления критерием Михайлова..9 5.2 Определение устойчивости системы управления критерием Найквиста..10 6 Определение качества процесса регулирования……………………………12 Индивидуальные условия к задачам…………………………………………..13 Приложение………………………………………………………………………19 1 Определение весовой функции ω (t)
Задача Модель элемента задана в виде передаточной функции Решение Весовая функция звена есть его реакция на дельта-функцию.
Чтобы выполнить обратное преобразование Лапласа, воспользуемся таблицей преобразований (см. Приложение 1). В таблице имеется выражение, которое совпадает по структуре с выражением в фигурных скобках
Приведем выражение в фигурных скобках к табличному виду, для этого необходимо применить основные теоремы Лапласа (Приложение 1), в данном случае теорему линейности, согласно которой все константы могут быть вынесены за знак обратного преобразования Лапласа.
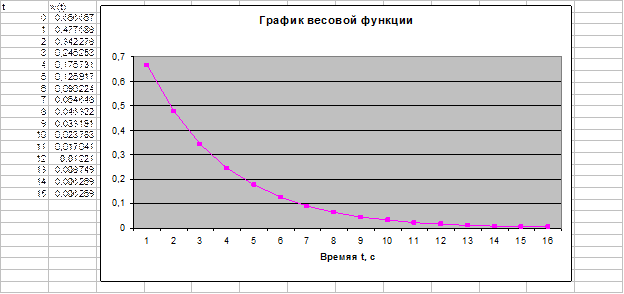
Получили выражение в фигурных скобках, в точности соответствующее табличному, где Тогда Задаваясь значениями t от 0 до ∞, можно получить график весовой функции. Однако даже при использовании вычислительной техники такой процесс является утомительным и зачастую так и не приводит к нужному результату. Поэтому следует вначале рассчитать начальное и конечное значения функции по предельным теоремам Лапласа (Приложение 1). Найдем начальное значение весовой функции согласно
Разделим каждое слагаемое числителя и знаменателя на максимальную степень переменной р и воспользуемся свойствами пределов: предел частного равен частному пределов, предел суммы равен сумме пределов и Исходя из этого имеем, что Аналогично получим конечное значение функции, согласно
Получены значения Составим таблицу и построим график функции. Данный расчет удобно выполнить в Приложении Microsoft Office в табличном редакторе Excel.
2 Определение переходной функции h (t) Задача Модель элемента задана в виде передаточной функции Решение Переходная функция звена есть его реакция на единичную ступенчатую функцию.
Выполним обратное преобразование Лапласа в соответствии с рекомендациями, изложенными в примере 1.
Рассчитаем начальное и конечное значения функции по предельным теоремам Лапласа:
Теперь можно определить момент окончания расчета. Это может быть любой момент времени, когда становится понятен характер изменения сигнала. Составим таблицу и построим график функции. Данный расчет удобно выполнить в Приложении Microsoft Office в табличном редакторе Excel.
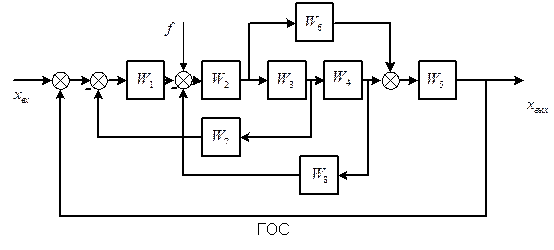
3 Структурные преобразования Задача Преобразовать схему и найти передаточные функции системы в разомкнутом и замкнутом состоянии по управляющему и возмущающему воздействиям, передаточные функции ошибок по управляющему и возмущающему воздействиям, характеристическое уравнение САУ в замкнутом состоянии.
Решение Для получения передаточной функции разомкнутой системы уберем главную обратную связь (ГОС). Далее проведем преобразования для упрощения схемы.
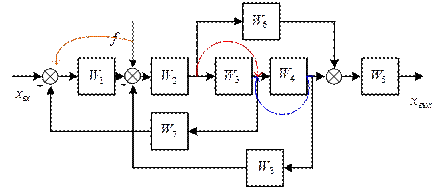
Первый шаг преобразования
и, кроме того, сделан перенос назад внешнего воздействия
Второй шаг преобразования
Третий шаг упрощения
Здесь динамическое звено W14 (p) является передаточной функцией разомкнутой системы по управляющему воздействию Wр (p). Передаточная функция по возмущающему воздействию определяется по формуле
Для определения передаточной функции замкнутой системы восстанавливаем ГОС.
Главная передаточная функция САУ имеет вид
Передаточная функция замкнутой системы для ошибки по задающему воздействию
Передаточная функция замкнутой системы по возмущающему воздействию
Передаточная функция для ошибки по возмущающему воздействию
Задача Определить устойчивость замкнутой системы управления, передаточная функция которой
Решение Характеристический полином системы
Матрица Гурвица будет иметь вид
Найдем определители матрицы
Если при заданной постоянной времени Т все определители матрицы Гурвица положительны, то делаем вывод об устойчивости замкнутой системы управления. В случае отрицательного значения хотя бы одного определителя делаем вывод о неустойчивости системы.
Задача Определить устойчивость замкнутой системы управления, передаточная функция которой
Решение Характеристический полином системы
Таблица Рауса будет иметь вид
Если при заданной постоянной времени Т все коэффициенты первого столбца таблицы Рауса положительны, то делаем вывод об устойчивости замкнутой системы управления. В случае отрицательного значения хотя бы одного коэффициенты делаем вывод о неустойчивости системы. Задача Определить устойчивость замкнутой системы управления, передаточная функция которой
Решение Характеристический полином системы
Заменим оператор дифференцирования p на (jω) и выделим вещественную и мнимую части
Решив системы уравнений, будут получены координаты для построения годографа.
Строим годограф.
Делаем вывод о неустойчивости системы управления, т.к. годограф не окружает начало координат. Задача Определить устойчивость замкнутой системы управления, разомкнутая передаточная функция которой Решение Характеристический полином разомкнутой системы
Найдем корни кубического уравнения.
Т.к. все корни имеют отрицательные вещественные части, делаем вывод об устойчивости системы в разомкнутом состоянии. Введем вспомогательную передаточную функцию W1 (p).
Построим годограф Михайлова для вспомогательной функции.
Делаем вывод о неустойчивости системы в замкнутом состоянии, т.к. годограф вспомогательной передаточной функции охватывает начало координат. Задача Определить качество процесса регулирования для автоматической системы, описываемой передаточной функцией
Решение Передаточная функция замкнутой системы будет равна
Корни характеристического полинома
равны
следовательно, степень устойчивости
Можно оценить время регулирования
Зная корни характеристического полинома, можно определить колебательность переходного процесса
количество колебаний
период колебаний переходного процесса равен
Время максимального перерегулирования определяется по формуле
Величина максимального перерегулирования
Приложение Таблица 3 – Фрагмент таблицы преобразования Лапласа
Основные свойства преобразования Лапласа 1. Теорема сложения Изображение суммы нескольких функций равно сумме изображений этих функций
и наоборот
2. Изображение функции, умноженной на константу Константа выносится за знак изображения
и наоборот
3. Изображение производной функции При нулевых начальных условиях изображение от производной функции n -го порядка равно произведению переменной
и наоборот
При ненулевых начальных условиях преобразование имеет следующий вид
где 4. Изображение от функции с запаздыванием Изображение от функции с запаздыванием τ равно произведению множителя
и наоборот
5. Теорема Лапласа о начальном значении
6. Теорема Лапласа о конечном значении
Содержание 1 Определение весовой функции ω (t)……………………………………………3 2 Определение переходной функции h (t)……………………………………….4 3 Структурные преобразования…………………………………………………5 4 Определение устойчивости системы управления алгебраическим критерием………………………………………………………………………….8 4.1 Определение устойчивости системы управления критерием Гурвица….8 4.2 Определение устойчивости системы управления критерием Рауса……..9 5 Определение устойчивости системы управления частотным критерием….9 5.1 Определение устойчивости системы управления критерием Михайлова..9 5.2 Определение устойчивости системы управления критерием Найквиста..10 6 Определение качества процесса регулирования……………………………12 Индивидуальные условия к задачам…………………………………………..13 Приложение………………………………………………………………………19 1 Определение весовой функции ω (t)
Задача Модель элемента задана в виде передаточной функции Решение Весовая функция звена есть его реакция на дельта-функцию.
Чтобы выполнить обратное преобразование Лапласа, воспользуемся таблицей преобразований (см. Приложение 1). В таблице имеется выражение, которое совпадает по структуре с выражением в фигурных скобках
Приведем выражение в фигурных скобках к табличному виду, для этого необходимо применить основные теоремы Лапласа (Приложение 1), в данном случае теорему линейности, согласно которой все константы могут быть вынесены за знак обратного преобразования Лапласа.
Получили выражение в фигурных скобках, в точности соответствующее табличному, где Тогда Задаваясь значениями t от 0 до ∞, можно получить график весовой функции. Однако даже при использовании вычислительной техники такой процесс является утомительным и зачастую так и не приводит к нужному результату. Поэтому следует вначале рассчитать начальное и конечное значения функции по предельным теоремам Лапласа (Приложение 1). Найдем начальное значение весовой функции согласно
Разделим каждое слагаемое числителя и знаменателя на максимальную степень переменной р и воспользуемся свойствами пределов: предел частного равен частному пределов, предел суммы равен сумме пределов и Исходя из этого имеем, что Аналогично получим конечное значение функции, согласно
Получены значения Составим таблицу и построим график функции. Данный расчет удобно выполнить в Приложении Microsoft Office в табличном редакторе Excel.
2 Определение переходной функции h (t) Задача Модель элемента задана в виде передаточной функции Решение Переходная функция звена есть его реакция на единичную ступенчатую функцию.
Выполним обратное преобразование Лапласа в соответствии с рекомендациями, изложенными в примере 1.
Рассчитаем начальное и конечное значения функции по предельным теоремам Лапласа:
Теперь можно определить момент окончания расчета. Это может быть любой момент времени, когда становится понятен характер изменения сигнала. Составим таблицу и построим график функции. Данный расчет удобно выполнить в Приложении Microsoft Office в табличном редакторе Excel.
3 Структурные преобразования Задача Преобразовать схему и найти передаточные функции системы в разомкнутом и замкнутом состоянии по управляющему и возмущающему воздействиям, передаточные функции ошибок по управляющему и возмущающему воздействиям, характеристическое уравнение САУ в замкнутом состоянии.
Решение Для получения передаточной функции разомкнутой системы уберем главную обратную связь (ГОС). Далее проведем преобразования для упрощения схемы.
Первый шаг преобразования
и, кроме того, сделан перенос назад внешнего воздействия
Второй шаг преобразования
Третий шаг упрощения
Здесь динамическое звено W14 (p) является передаточной функцией разомкнутой системы по управляющему воздействию Wр (p). Передаточная функция по возмущающему воздействию определяется по формуле
Для определения передаточной функции замкнутой системы восстанавливаем ГОС.
Главная передаточная функция САУ имеет вид
Передаточная функция замкнутой системы для ошибки по задающему воздействию
Передаточная функция замкнутой системы по возмущающему воздействию
Передаточная функция для ошибки по возмущающему воздействию
Определение устойчивости системы управления алгебраическим критерием Алгебраический критерий позволяет определять устойчивость системы управления по коэффициентам характеристического полинома без вычисления его корней.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 . Требуется построить график весовой функции
. Требуется построить график весовой функции 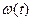 данного элемента.
данного элемента.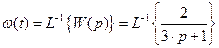 .
.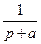 .
.
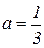 .
.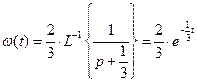 .
.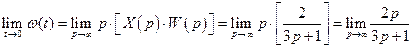 .
. .
.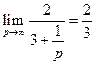 .
. .
. и
и 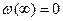 .
.
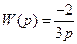 . Требуется построить график переходной функции
. Требуется построить график переходной функции 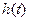 данного элемента.
данного элемента.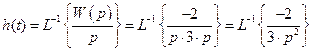 .
. .
. ;
;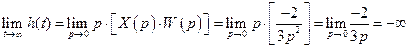 .
.
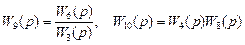 ,
, .
.
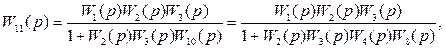


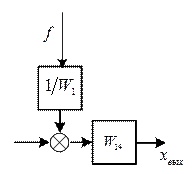
 ,
, .
.
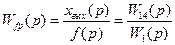 .
.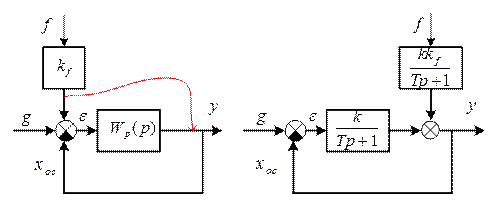
 .
.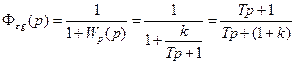 .
.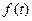 определяется при условии равенства нулю задающего воздействия
определяется при условии равенства нулю задающего воздействия 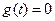 и равна
и равна .
. будет той же, что передаточная функция замкнутой системы по возмущающему воздействию
будет той же, что передаточная функция замкнутой системы по возмущающему воздействию  , но с обратным знаком
, но с обратным знаком .
. , используя алгебраический критерий устойчивости Гурвица.
, используя алгебраический критерий устойчивости Гурвица. .
.
 ;
; ;
; .
.



 .
. .
. ,
,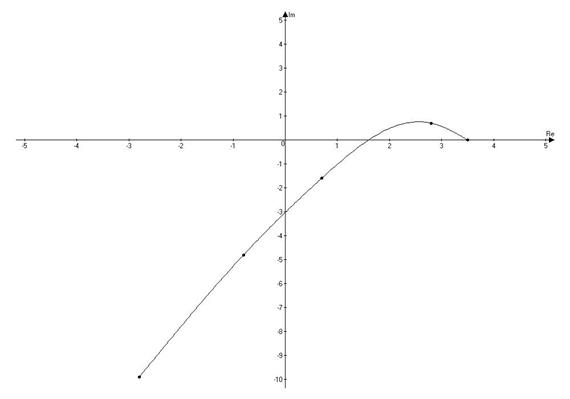
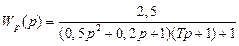 , при Т = 1, используя частотный критерий устойчивости Найквиста.
, при Т = 1, используя частотный критерий устойчивости Найквиста. .
.
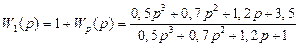 .
.
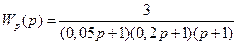 .
. .
.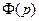

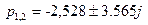 ,
, 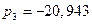 .
. .
.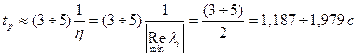 .
.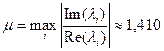 .
. за время переходного процесса
за время переходного процесса  не превышает
не превышает .
.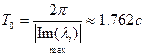 .
. .
. оценивается по формуле
оценивается по формуле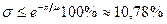 .
.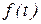



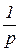


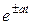




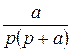
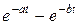
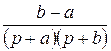
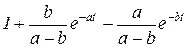



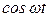
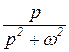


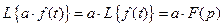 ,
,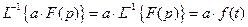 .
.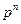 на изображение исходной функции
на изображение исходной функции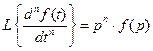 ,
, .
.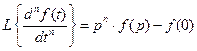 ,
, - значение функции
- значение функции 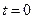 .
.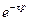 на изображение исходной функции
на изображение исходной функции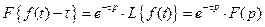 ,
, .
.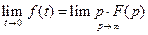 .
. .
.


