
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение устойчивости системы управления критерием ГурвицаСодержание книги
Поиск на нашем сайте
Задача Определить устойчивость замкнутой системы управления, передаточная функция которой
Решение Характеристический полином системы
Матрица Гурвица будет иметь вид
Найдем определители матрицы
Если при заданной постоянной времени Т все определители матрицы Гурвица положительны, то делаем вывод об устойчивости замкнутой системы управления. В случае отрицательного значения хотя бы одного определителя делаем вывод о неустойчивости системы.
Определение устойчивости системы управления критерием Рауса Задача Определить устойчивость замкнутой системы управления, передаточная функция которой
Решение Характеристический полином системы
Таблица Рауса будет иметь вид
Если при заданной постоянной времени Т все коэффициенты первого столбца таблицы Рауса положительны, то делаем вывод об устойчивости замкнутой системы управления. В случае отрицательного значения хотя бы одного коэффициенты делаем вывод о неустойчивости системы. Определение устойчивости системы управления частотным критерием Определение устойчивости системы управления критерием Михайлова Задача Определить устойчивость замкнутой системы управления, передаточная функция которой
Решение Характеристический полином системы
Заменим оператор дифференцирования p на (jω) и выделим вещественную и мнимую части
Решив системы уравнений, будут получены координаты для построения годографа.
Строим годограф.
Делаем вывод о неустойчивости системы управления, т.к. годограф не окружает начало координат. Определение устойчивости системы управления критерием Найквиста Задача Определить устойчивость замкнутой системы управления, разомкнутая передаточная функция которой Решение Характеристический полином разомкнутой системы
Найдем корни кубического уравнения.
Т.к. все корни имеют отрицательные вещественные части, делаем вывод об устойчивости системы в разомкнутом состоянии. Введем вспомогательную передаточную функцию W1 (p).
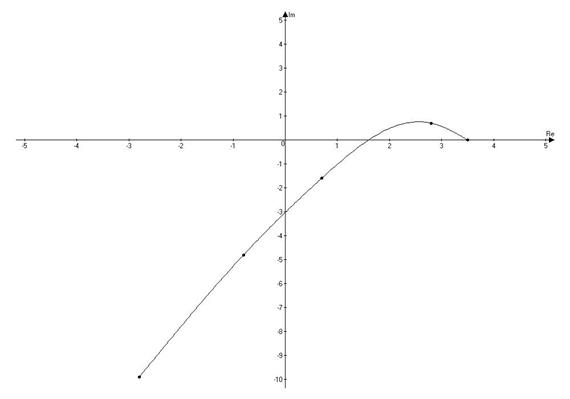
Построим годограф Михайлова для вспомогательной функции.
Делаем вывод о неустойчивости системы в замкнутом состоянии, т.к. годограф вспомогательной передаточной функции охватывает начало координат.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.199.54 (0.005 с.) |

 , используя алгебраический критерий устойчивости Гурвица.
, используя алгебраический критерий устойчивости Гурвица. .
.
 ;
; ;
; .
.



 .
. .
. ,
,
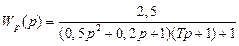 , при Т = 1, используя частотный критерий устойчивости Найквиста.
, при Т = 1, используя частотный критерий устойчивости Найквиста. .
.
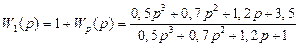 .
.



