
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение качества процесса регулированияСодержание книги
Поиск на нашем сайте
Задача Определить качество процесса регулирования для автоматической системы, описываемой передаточной функцией
Решение Передаточная функция замкнутой системы будет равна
Корни характеристического полинома
равны
следовательно, степень устойчивости
Можно оценить время регулирования
Зная корни характеристического полинома, можно определить колебательность переходного процесса
количество колебаний
период колебаний переходного процесса равен
Время максимального перерегулирования определяется по формуле
Величина максимального перерегулирования
Индивидуальные условия к задачам Таблица 1 – Исходные данные к задачам раздела 1 и 2
Исходные данные к задаче раздела 3 Структурные схемы линейной САУ 1.
2.
3.
4.
5.
6.
Таблица 2 - Параметры структурной схемы САУ
Приложение Таблица 3 – Фрагмент таблицы преобразования Лапласа
Основные свойства преобразования Лапласа 1. Теорема сложения Изображение суммы нескольких функций равно сумме изображений этих функций
и наоборот
2. Изображение функции, умноженной на константу Константа выносится за знак изображения
и наоборот
3. Изображение производной функции При нулевых начальных условиях изображение от производной функции n -го порядка равно произведению переменной
и наоборот
При ненулевых начальных условиях преобразование имеет следующий вид
где 4. Изображение от функции с запаздыванием Изображение от функции с запаздыванием τ равно произведению множителя
и наоборот
5. Теорема Лапласа о начальном значении
6. Теорема Лапласа о конечном значении
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.203.129 (0.008 с.) |

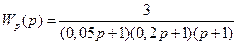 .
. .
.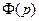

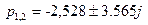 ,
, 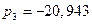 .
. .
.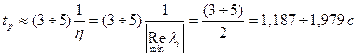 .
.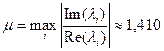 .
. за время переходного процесса
за время переходного процесса  не превышает
не превышает .
.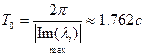 .
. .
. оценивается по формуле
оценивается по формуле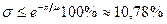 .
. функции
функции
 функции
функции
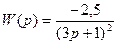

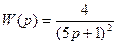

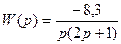






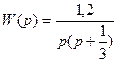


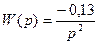
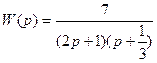

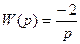





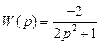


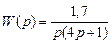

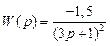

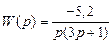


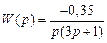




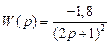






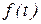



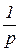


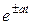




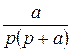
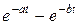
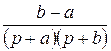
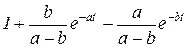



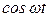
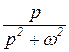


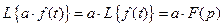 ,
,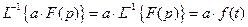 .
.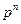 на изображение исходной функции
на изображение исходной функции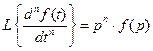 ,
, .
.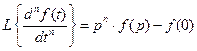 ,
, - значение функции
- значение функции 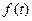 при
при 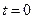 .
.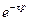 на изображение исходной функции
на изображение исходной функции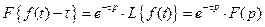 ,
, .
.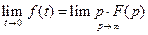 .
. .
.


