
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи и методы исследования устойчивости.Содержание книги
Поиск на нашем сайте
Задачи и методы исследования устойчивости. В первых двух частях курса строительной механики изучаются методы определения усилий и перемещений в элементах стержневых систем от действия статических нагрузок. Эти методы позволяют получить картину распределения усилий в конструкции при расчете ее на прочность. Однако во многих случаях расчет на прочность является недостаточным, чтобы судить о надежности сооружения. В особенности это относится к таким сооружениям, которые состоят из гибких сжатых и сжатоизогнутых элементов. Как правило, для таких сооружений решающим фактором, определяющим их несущую способность, является возможность потери устойчивости сооружения в целом или же отдельных его элементов. Устойчивостью сооружений называется их свойство сохранять свою первоначальную форму равновесия в деформированном состоянии, всегда пребывать при любых малых посторонних возмущениях близко к исходному невозмущенному состоянию и возвращаться к нему в упругой стадии полностью, а в упругопластической полностью или частично, если случайные причины, вызвавшие возмущение сооружения, исчезают. В теории устойчивости сооружений рассматриваются принципы и методы определения величин нагрузок, при действии которых системы переходят в неустойчивое состояние, а также тех конечных перемещений, которые наблюдаются после потери устойчивости.
Виды потери устойчивости. Потеря устойчивости может быть двух видов; 1) потеря устойчивости положения и 2) потеря устойчивости форм равновесия в деформированном состоянии. Могут быть устойчивые и неустойчивые положения сооружения, устойчивые и неустойчивые формы равновесия в деформированном состоянии всего сооружения или отдельных его элементов. Положение сооружения и форма равновесия в деформированном состоянии считаются устойчивыми, если сооружение или отдельные его элементы, выведенные из первоначального состояния какими-либо силами, после снятия этих сил возвращаются в исходное состояние. Положение и форма равновесия сооружения в деформированном состоянии считаются неустойчивыми, если хотя бы при каком-либо малом возможном отклонений от исследуемого равновесия сооружение, будучи предоставлено самому себе, уже не вернется в исходное состояние, а иногда будет отклоняться еще далее - до нового положения или новой формы равновесия. Потеря устойчивости положения относится к случаю, когда сооружение в целом не может дальше сохранять свое первоначальное положение и вынуждено его изменить. Потеря устойчивости формы равновесия в деформированном состоянии относится к случаю, когда первоначальная форма деформации тел, у которых хотя бы одно из трех измерений мало по сравнению с двумя другими, соответствующая малым начальным нагрузкам, при некотором значении этих нагрузок становится неустойчивой и вынуждено переходить в другую форму, качественно отличную от первоначальной. Наступает разветвление теоретически возможных, по крайней мере, двух форм равновесия, одна из которых неустойчива. Например, длинный прямой стержень, сжимаемый по концам двумя силами, при некотором значении, этих сил становится неустойчивым и. при малых посторонних воздействиях искривляется / рис. I /;симметрично нагруженная арка меняет свою вначале симметричную форму деформации на косую / рис. 2 /; тонкая полоса, изгибаемая в плоскости наибольшей жесткости, при некоторой нагрузке начинает изгибаться косо и закручивается/рис.3/.
Нагрузка, приводящая к переходу системы из состояния устойчивого равновесия в новое состояние равновесия, которое может быть как устойчивым, так и неустойчивым, называется критической нагрузкой. Обычно после потери устойчивости во второй форме равновесия малым приращением нагрузки соответствуют большие перемещения. Различают потери устойчивости первого и второго родов. Потеря устойчивости первого рода сопровождается сменой формы деформированного состояния. Примером потери устойчивости первого рода является продольный изгиб прямолинейного стержня, сжатого осевой силой или потеря устойчивости плоской формы изгиба балки. Здесь возникает новый вид деформации - изгиб стержня и скручивание балки. При потере устойчивости второго рода качественно сохраняется характер развития деформация на всем протяжении процесса деформирования. Примером потери устойчивости второго рода является продольный изгиб внецентренно сжатого стержня, продольный изгиб при наличии поперечной нагрузки, потеря устойчивости сжато-изогнутой рамы или арки и т.д. Задачей устойчивости сооружений является расчет сооружений главным образом на устойчивость первого рода. При этом будем рассматривать устойчивость только консервативных систем, т.е. линейно-деформируемых систем. Число возможных форм неустойчивого равновесия определяется степенью свободы системы. Степенью свободы системы с точки зрения устойчивости называется число независимых геометрических параметров, определяющих положение всех точек системы, потерявшей устойчивость. Система с конечным числом степеней свободы - это система, расчетная схема которой представляет конечное число бесконечно жестких элементов, соединенных между собой упругими связями. Число степеней свободы может быть определено по формуле
Существуют три основных метода определения критических сил: статический, энергетический и динамический.
Задачи и методы исследования устойчивости. В первых двух частях курса строительной механики изучаются методы определения усилий и перемещений в элементах стержневых систем от действия статических нагрузок. Эти методы позволяют получить картину распределения усилий в конструкции при расчете ее на прочность. Однако во многих случаях расчет на прочность является недостаточным, чтобы судить о надежности сооружения. В особенности это относится к таким сооружениям, которые состоят из гибких сжатых и сжатоизогнутых элементов. Как правило, для таких сооружений решающим фактором, определяющим их несущую способность, является возможность потери устойчивости сооружения в целом или же отдельных его элементов. Устойчивостью сооружений называется их свойство сохранять свою первоначальную форму равновесия в деформированном состоянии, всегда пребывать при любых малых посторонних возмущениях близко к исходному невозмущенному состоянию и возвращаться к нему в упругой стадии полностью, а в упругопластической полностью или частично, если случайные причины, вызвавшие возмущение сооружения, исчезают. В теории устойчивости сооружений рассматриваются принципы и методы определения величин нагрузок, при действии которых системы переходят в неустойчивое состояние, а также тех конечных перемещений, которые наблюдаются после потери устойчивости.
Виды потери устойчивости. Потеря устойчивости может быть двух видов; 1) потеря устойчивости положения и 2) потеря устойчивости форм равновесия в деформированном состоянии. Могут быть устойчивые и неустойчивые положения сооружения, устойчивые и неустойчивые формы равновесия в деформированном состоянии всего сооружения или отдельных его элементов. Положение сооружения и форма равновесия в деформированном состоянии считаются устойчивыми, если сооружение или отдельные его элементы, выведенные из первоначального состояния какими-либо силами, после снятия этих сил возвращаются в исходное состояние. Положение и форма равновесия сооружения в деформированном состоянии считаются неустойчивыми, если хотя бы при каком-либо малом возможном отклонений от исследуемого равновесия сооружение, будучи предоставлено самому себе, уже не вернется в исходное состояние, а иногда будет отклоняться еще далее - до нового положения или новой формы равновесия. Потеря устойчивости положения относится к случаю, когда сооружение в целом не может дальше сохранять свое первоначальное положение и вынуждено его изменить. Потеря устойчивости формы равновесия в деформированном состоянии относится к случаю, когда первоначальная форма деформации тел, у которых хотя бы одно из трех измерений мало по сравнению с двумя другими, соответствующая малым начальным нагрузкам, при некотором значении этих нагрузок становится неустойчивой и вынуждено переходить в другую форму, качественно отличную от первоначальной. Наступает разветвление теоретически возможных, по крайней мере, двух форм равновесия, одна из которых неустойчива. Например, длинный прямой стержень, сжимаемый по концам двумя силами, при некотором значении, этих сил становится неустойчивым и. при малых посторонних воздействиях искривляется / рис. I /;симметрично нагруженная арка меняет свою вначале симметричную форму деформации на косую / рис. 2 /; тонкая полоса, изгибаемая в плоскости наибольшей жесткости, при некоторой нагрузке начинает изгибаться косо и закручивается/рис.3/.
Нагрузка, приводящая к переходу системы из состояния устойчивого равновесия в новое состояние равновесия, которое может быть как устойчивым, так и неустойчивым, называется критической нагрузкой. Обычно после потери устойчивости во второй форме равновесия малым приращением нагрузки соответствуют большие перемещения. Различают потери устойчивости первого и второго родов. Потеря устойчивости первого рода сопровождается сменой формы деформированного состояния. Примером потери устойчивости первого рода является продольный изгиб прямолинейного стержня, сжатого осевой силой или потеря устойчивости плоской формы изгиба балки. Здесь возникает новый вид деформации - изгиб стержня и скручивание балки. При потере устойчивости второго рода качественно сохраняется характер развития деформация на всем протяжении процесса деформирования. Примером потери устойчивости второго рода является продольный изгиб внецентренно сжатого стержня, продольный изгиб при наличии поперечной нагрузки, потеря устойчивости сжато-изогнутой рамы или арки и т.д. Задачей устойчивости сооружений является расчет сооружений главным образом на устойчивость первого рода. При этом будем рассматривать устойчивость только консервативных систем, т.е. линейно-деформируемых систем. Число возможных форм неустойчивого равновесия определяется степенью свободы системы. Степенью свободы системы с точки зрения устойчивости называется число независимых геометрических параметров, определяющих положение всех точек системы, потерявшей устойчивость. Система с конечным числом степеней свободы - это система, расчетная схема которой представляет конечное число бесконечно жестких элементов, соединенных между собой упругими связями. Число степеней свободы может быть определено по формуле
Существуют три основных метода определения критических сил: статический, энергетический и динамический.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 803; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.68 (0.007 с.) |



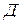 -число элементов с бесконечной жесткостью.
-число элементов с бесконечной жесткостью. 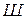 -число простых шарниров,
-число простых шарниров,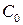 -число опорных связей. Упругие связи не учитываются.
-число опорных связей. Упругие связи не учитываются.


