
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициентов канонических уравнений метода перемещений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Канонические уравнения метода перемещений при расчете на устойчивость являются однородными, поэтому возможны два решения системы уравнений. Первое решение, когда все неизвестные равны нулю,
этому решению соответствует первоначальная форма деформации рамы, т.е. отсутствие изгиба. Такое решение для нас' неприемлемо. Второе решение, когда все или часть неизвестных отличны от нуля. Этому случаю соответствует потеря устойчивости первоначальной формы деформации рамы. Это условие будет выражаться равенством нулю определителя, составленного из коэффициентов при неизвестных.
Раскрывая определитель, полупим уравнение, которое в аналитической форме вырастает условие критического состояния рамы. Таким образом, решение уравнений не дает значения неизвестных поворота и линейных смещений узлов. Эти неизвестные так и остаются неопределенными. Однако, возможно найти их соотношения. Так, например, задаваясь значением деформации рамы в момент потери устойчивости. Получив уравнение критического состояния рамы и найдя его наименьший положительный корень, можно определять значение критической силы для каждого стержня рамы. 14. Метод Тимошенко определения критических нагрузок. В основе этого метода положено равенство изменений энергии внешних и внутренних сил системы при небольшом отклонении ее от состояния равновесия
Для определения
который полностью или частично должно удовлетворять граничным условиям. Здесь Далее определяются производные
Параметры
Условия экстремума дают нам n линейных однородных уравнений для определения параметров. Решая эти уравнения, находим значения параметров
Пример:
Определить
Ограничимся двумя членами ряда, тогда при при
т.е. граничные условия выполнены частично. Определяем изменение энергии внутренних сил
Рис.28 Определяем изменение энергия внешних сил
Приравниваем
Обозначим
Составляем условие
Корни этого уравнения Минимальное значение сила Р имеет при Точное решение, как известно, дает значение
15. Метод Ритца определения Pкр. В основу этого метода положено условие, что в состоянии устойчивого равновесия потенциальная энергия упругой системы имеет минимальное значение. Полная потенциальная энергия упругой системы определяется как сумма работ внешних я внутренних сил при переходе системы из деформированного состояние в первоначальное.
Для определения потенциальной энергии форму упругой кривой рекомендуется принимать в виде ряда
где Далее определяются значения
которая будет функцией неопределенных параметров
Для того, чтобы функция потенциальной энергия имела экстремальное значение, необходимо, чтобы ее частные производные по па- раметрам
Получаем систему n линейных однородных уравнений относительно приравнять нулю определитель из коэффициентов при неизвестных
Раскрывая определитель, получаем уравнение для определения критической нагрузки. Рассмотрим предыдущий пример, задаваясь для
Работа внутренних сил
Работа внешних сил Полная потенциальная энергия системы
Тогда условие экстремума
или
Приравнивая нулю определитель из коэффициентов
Наименьший корень этого уравнения
16. Метод Бубнова-Галеркина определения Pкр. При определении критической силы этим методом не требуется составлять выражение для потенциальной энергии системы. Исходным пункт при этом является дифференциальное уравнение изогнутой оси стержня. Для случая, когда стержень подвергнут только действию продольной сжимающей силы, дифференциальное уравнение изгиба в общем виде будет
Для решения уравнения / 9 / методом Бубнова-Галеркина форма упругой линии стержня при потере устойчивости задаётся приближенным выражением в виде ряда где Дифференциальное уравнение
или Приближенное решение довольствуется тем, чтобы обратить /II/ в нуль n раз, т.е. для n выбранных функций принимаются функции, входящие в разложение /10/. Подставляя в уравнение /II/ выражения для y, получаем n независимых линейных уравнений для определения параметров:
Пример:
Определить
Для упрощения расчетов примем
Тогда
Рис.29
Система /12/ превращается в одно уравнение
Тогда или
Отсюда Точное решение дает значение Погрешность приближенного значения составляет ~ 4%.
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.220 (0.009 с.) |

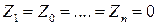

 углов
углов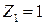 можно из остальных уравнений системы получить значения остальных неизвестных в долях от
можно из остальных уравнений системы получить значения остальных неизвестных в долях от 
 форму упругой линии рекомендуется принимать в виде многочлена
форму упругой линии рекомендуется принимать в виде многочлена
 - неопределенные параметры, которые подлежат определению.
- неопределенные параметры, которые подлежат определению. и составляются выражения для
и составляются выражения для 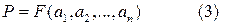
 подбираем таким образом, чтобы сила P имела минимальное значение, т. е. составляем условия экстремума функции P
подбираем таким образом, чтобы сила P имела минимальное значение, т. е. составляем условия экстремума функции P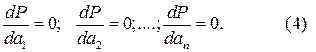


 для данной стойки. Задаёмся
для данной стойки. Задаёмся  в виде ряда
в виде ряда
 ,
, , в то время как
, в то время как
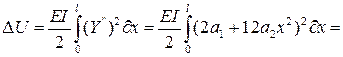


 , откуда
, откуда
 , тогда
, тогда
 , которое приводит к квадратному уравнению
, которое приводит к квадратному уравнению .
.
 , поэтому подставляя
, поэтому подставляя 
 , погрешность составляет 0,1%.
, погрешность составляет 0,1%.

 - неопределенные параметры,
- неопределенные параметры,  -функции, удовлетворяющие полностью или частично граничным условиям.
-функции, удовлетворяющие полностью или частично граничным условиям. и составляются выражения для потенциальной энергии
и составляются выражения для потенциальной энергии



 тем же выражением
тем же выражением



 дадут:
дадут:


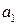 при
при  , получим квадратное уравнение для определения Р
, получим квадратное уравнение для определения Р

 .
.

 - функций, удовлетворяющие всем граничным условиям стержня и отвечающие представлению о возможных формах потери устойчивости. Коэффициенты
- функций, удовлетворяющие всем граничным условиям стержня и отвечающие представлению о возможных формах потери устойчивости. Коэффициенты  должно удовлетворяться при любых значениях переменных x в пределах длины стержня. Поэтому для любой функции
должно удовлетворяться при любых значениях переменных x в пределах длины стержня. Поэтому для любой функции 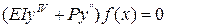



 , которая отвечает загружению балки сплошной равномерной поперечной нагрузкой
, которая отвечает загружению балки сплошной равномерной поперечной нагрузкой


 .
.




 .
.


