
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение опорных реакций составной балкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте С элементами оптимизации
Задача С5
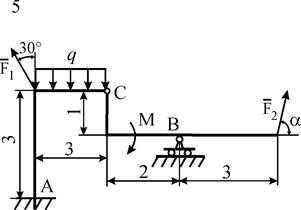
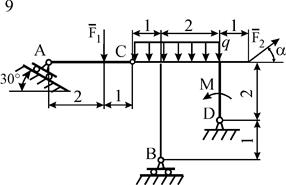
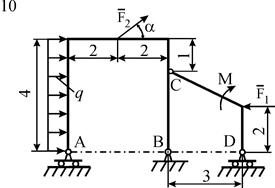
Схемы конструкций изображены на рис. С5.1–С5.4. Исходные данные приведены в табл. С5. Во всех вариантах сила
Методика решения задачи с элементами оптимизации
Решить поставленную задачу – значит найти лучший вариант проектируемого объекта, например, конструкции машины или сооружения, технологического процесса и др. В данном случае решение задачи оптимизации сводится к определению значений угла a, при которых рассматриваемая конструкция оказывается лучшей по одному из двух критериев: или одна из исследуемых опор должна иметь минимальный вес, или все опоры должны деформироваться с минимальной потенциальной энергией. Последнее эквивалентно, например, минимальному нагреву опоры, обусловленному ее деформацией. Критерий минимального веса опоры
Для упрощения задачи представим все опоры в виде стержней заданной длины, расположенных вдоль составляющих сил реакций. Таким образом каждый стержень будет нагружен некоторой продольной силой Модуль силы
где S – площадь поперечного сечения стержня, s – сила, приходящаяся на единицу этой площади. Умножим и разделим правую часть равенства (25) на длину l стержня и удельный вес g материала, из которого он изготовлен. Получим
где G – вес стержня, l* = l ×g/s.
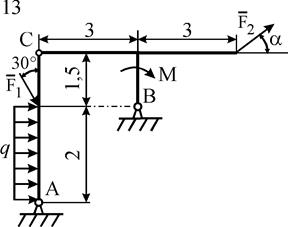
Рис. С5.1
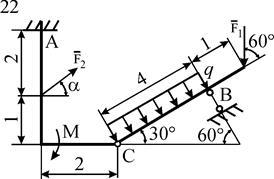
Рис. С5.2
Рис. С5.3
Рис. С5.4
Таблица С5
Как видно, при заданном коэффициенте l* оптимизацию по весу стержня можно заменить оптимизацией по силе В тех вариантах задачи, где опора A представляет собой жесткую заделку, роль силы
В данной задаче в результате решения соответствующей системы уравнений равновесия находят RA как функцию одного аргумента a. Оптимальное значение реакции найдется из исследования функции RA на глобальный экстремум, в данном случае глобальный минимум (глобальным минимумом функции называется наименьшее ее значение в изучаемом интервале изменения аргумента). Численные значения реакций всех опор зависят от sin a и cos a, которые имеют период 2p. Это позволяет ограничиться поиском глобального минимума RA в интервале изменения аргумента a:
Значения RA вычисляются с интервалом Da = p/12 в соответствии с формулой
Критерий минимальной потенциальной энергии деформации
По-прежнему опоры представляем стержнями, работающими по направлениям составляющих реакций. Из курса физики известно, что потенциальная энергия П i деформации i -го стержня, нагруженного продольной силой N i, равна
где Деформация определяется согласно закону Гука:
Здесь Подставив (28) в (27), найдем потенциальную энергию стержня в виде
где коэффициент В дальнейшем величина
Как видно, при известном коэффициенте
где X i – модуль i -й составляющей реакции соответствующей опоры. Следует отметить, что в числе модулей реакций могут быть как силы, так и моменты пар сил. Для приведения тех и других к одной размерности значения X i, соответствующие моментам, необходимо разделить на характерный габаритный размер h конструкции. Во всех вариантах задания величину h принять равной 1м. С помощью найденных выше значений X i определяется целевая функция с шагом Da = p/12. По вычисленной целевой функции строится график f (a) в интервале
Пример выполнения задания
Постановка задачи и получение расчетных формул
На рис.С5а представлена схема составной конструкции, два элемента которой (АС и СВ) соединены между собой цилиндрическим шарниромC. На конструкцию в целом наложены внешние связи в виде шарнирно-неподвижных опор A и B и внутренняя связь в шарнире С. Размеры элементов указаны в метрах. Дано: F1 = 10 кH, F2 = 7,0 кН, М = 11 кН×м, q = 1 кН/м, b = 600. Определить, при каких значениях угла a опора А будет иметь наименьший вес и потенциальная энергия деформации всех опор минимальной. Решение. Заменим равномерно распределенную нагрузку интенсивностью q равнодействующей Расчленим заданную конструкцию на два элемента АС и СВ, представленные на рис. С5б и рис. С5в соответственно.
Рис. С5а
Рис. С5б Рис. С5в
К каждому элементу прикладываем заданные активные силы и реакции внешних и внутренней связей. Примем для обоих элементов единую систему координат О xy. В точке А элемента АС прикладываем составляющие (компоненты) Составим уравнения, выражающие равновесие элемента АС:
Составим уравнения равновесия элемента ВС:
С учетом, что
Система уравнений (38) позволяет определить реакции связей как функции угла a ( С целью упрощения уравнений (38) подставим числовые значения заданных постоянных величин:
Матричная форма уравнений равновесия Правые части уравнений (39) имеют вид
Представим систему уравнений (39) в матричной форме:
где X – матрица-столбец неизвестных,
A – матрица коэффициентов при неизвестных,
матрица-столбец правых частей системы уравнений (39)
Для любого варианта задания каждый элемент этого столбца может иметь вид В матрицах (43) и (44) целые числа являются точными, дробное число должно быть записано с относительной погрешностью, соответствующей пяти верным значащим цифрам. Такая же запись промежуточных результатов должна быть сохранена во всех вариантах задания. Она вытекает из принятой в инженерной практике точности расчетов в 5 %, что соответствует записи окончательных результатов с тремя верными значащими цифрами. Решением матричного уравнения (41) будет
где А-1 – матрица, обратная матрице А.
Алгоритм вычислений Для решения матричного уравнения (41) в Mathcad имеется функция lsolve (A, B), которая возвращает вектор Х для системы уравнений А×Х = В при заданной матрице коэффициентов А и векторе свободных членов В. В нашей задаче матрица В является переменной, зависящей от угла a. Выбираем шаг изменения угла Da = p/12. Модули реакций в точках определяются через составляющие
Из графика R i (a) находим значение угла, при котором данная реакция имеет минимум.
Результаты вычислений Значения модулей составляющих реакций всех связей полной искомой реакции должны быть сведены в табл. С5.1.
Таблица С5.1
По данным табл. С5.1 вначале строим график RA в функции от угла a (рис. C5г). Для этого наносим на координатную плоскость RA – a точки, соответствующие вычисленным значениям реакции. Полученные точки соединяем плавной кривой. На этой кривой отмечаем точку, соответствующую значению глобального минимума реакции RAmin и по ней находим значение amin, т. е. угла a, соответствующего значению RAmin.
Рис. С5г
Рис. С5д
Примечание. В тех вариантах задания, где в точке A расположена шарнирно-подвижная опора или невесомый стержень, кривая зависимости RA = RA(a) может пересекать ось a и часть ее располагаться ниже этой оси (рис. С5д). Это означает, что для этой части кривой значения модулей оказались отрицательными. Эта часть графика показана пунктиром. Поскольку модуль не может быть отрицательным, нижнюю часть графика следует зеркально перенести вверх относительно оси a. Точки пересечения кривой (сплошной и пунктирной) с осью a дают значения углов (amin)1, (amin)2, соответствующих значению реакции RA, равное нулю (глобальный минимум). Для оценки оптимальности конструкции по второму критерию строим график изменения сумм квадратов модулей составляющих реакции в зависимости от угла a (рис. С5е).
Рис. С5е
На графике отмечаем точку A, соответствующую глобальному минимуму целевой функции f (a) и определяем угол amin.
Содержание отчета Отчет по работе должен содержать: 1) схему конструкции, исходные данные и постановку задачи; 2) изложение расчета с расчетными схемами и краткими пояснениями (уравнениями равновесия, решение уравнений в общем виде, запись целевых функций, методику нахождения оптимального угла a); 3) схему алгоритма, программу; 4) распечатку числовых результатов, графики, анализ результатов.
Вычисляем потенциальную энергию деформации:
П (a) = (Х(a)1)2 + (Х(a)2)2 + (Х(a)3)2 + (Х(a)4)2 + (Х(a)5)2 + (Х(a)6)2.
Таблица C5.2
Рис. С5ж
Рис. С5з
Табл. С5.2 содержит результаты вычислений, а на рис. С5ж и С5з представлены графики зависимостей RA = RA(a) и П = П(a), построенные по этим результатам. КИНЕМАТИКА Кинематика точки
Определить движение точки - это значит уметь определить положение точки по отношению к выбранной системе отсчета в любой момент времени. В кинематике применяются три способа задания движения точки: векторный, координатный и естественный. При векторном способе определения движения точки радиус-вектор движущейся точки М (рис. 21), проведенный из выбранного неподвижного центра О, выражается как векторная функция от времени, т. е.
Скорость
Ускорение
Координатный способ определения (задания) движения точки состоит в том, что координаты движущейся точки в выбранной системе координат выражаются как функции времени t. Уравнения движения точки в декартовых координатах имеют вид
x = x (t), y = y (t), z = z (t).
Если точка движется в плоскости О ху, то будем иметь только два уравнения движения:
x = x (t), y = y (t).
Для того чтобы найти траекторию точки, достаточно из уравнений движения исключить время t. Вектор скорости и вектор ускорения определяются по их проекциям на оси декартовых координат, причем
Отсюда получаем формулы разложения векторов скорости
Модули векторов скорости и ускорения вычисляем по формулам
При естественном способе движение точки задается ее траекторией и уравнением движения по этой траектории:
где О - начало отсчета дуг на траектории; s - дуговая координата точки М или взятая с соответствующим знаком длина дуги, отсчитываемая вдоль траектории от начала отсчета до точки М (рис. 22).
Рис. 22 Если заданы траектория движущейся точки и закон ее движения по этой траектории s = s (t), то вектор скорости направлен по касательной к этой траектории, а его проекция на направление касательной определяется по формуле
причем абсолютное значение этой проекции равно модулю скорости:
Вектор ускорения определяется по его проекциям на естественные оси (касательную, главную нормаль и бинормаль):
где r - радиус кривизны траектории в данной точке. Следовательно,
Отметим частные случаи: 1. Если точка движется прямолинейно и неравномерно, то радиус кривизны траектории r ® µ и, следовательно, а n = 0. В этом случае ускорение направлено вдоль траектории точки и по модулю равно
2. Если точка движется по криволинейной траектории равномерно, то
V = const и
и поэтому ускорение направлено по нормали к траектории и по модулю равно
3. Если точка движется прямолинейно и равномерно, то a n = 0, a t = 0 и a = 0. В том случае, когда движение точки задано в координатной форме, касательное ускорение определяется по формуле
После этого нормальное ускорение можно найти из равенства
где Определив
Если плоская траектория задана уравнением у = у (х), то радиус кривизны траектории вычисляется по формуле
где
Задача K1
Точка M движется в плоскости ху (рис. K1.0–K1.9, табл. K1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями х = f 1(t), у = f 2(t), где х и у выражены в сантиметрах, t – в секундах. Найти уравнение траектории точки; для момента времени t = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Зависимость х = f (t) указана непосредственно на рисунках, а зависимость у = f 2(t) дана в табл. K1 (для рис. K1.0–K1.2 - в столбце 2, для рис. K1.3–K1.6 - в столбце 3, для рис. K1.7–K1.9 - в столбце 4). Указания. Задача K1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.
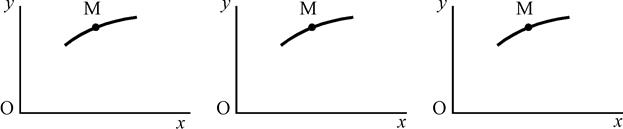
Рис. К1.0 Рис. К1.1 Рис. К1.2

Рис. К1.3 Рис. К1.4 Рис. К1.5

Рис. К1.6 Рис. К1.7 Рис. К1.8
Таблица K1
В задаче все искомые величины нужно определить только для момента времени t1 = 1 с. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:
сos 2a = 1 – 2 sin2 a = 2 cos2 a – 1; sin 2a = 2×sin a×cos a.
Пример K1. Даны уравнения движения точки в плоскости ху:
x = 6×cos (p×t/6) – 3, y = – 4×cos2 (p×t/6)
(х, у - в метрах, t - в секундах). Определить уравнение траектории точки. Для момента времени t1 = 1 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Решение. Для определения траектории исключим из заданных уравнений движения время t, воспользовавшись подстановкой:
Из полученного выражения следует, что траекторией движения точки является парабола с нисходящими ветвями и осью, параллельной оси у; вершина параболы находится в точке с координатами х = -3 м, у = 0. Найдем проекции вектора скорости на оси координат:
Подставив t1 = 1 с в полученные выражения, находим
Скорость точки в момент времени t1 = 1 с
Найдем проекции вектора ускорения:
Для момента времени t1 = 1 с
Касательное ускорение найдем по формуле
Нормальное ускорение
Вычислим радиус кривизны траектории в том месте, где находится точка в момент времени t1 = 1 с:
Рис. K1
Пользуясь уравнением траектории, вычерчиваем параболу (рис. K1) и показываем на ней точку М в заданный момент времени по ее координатам. Вектор скорости | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 наклонена к оси x под углом a, который изменяется от 0 до 2p. Требуется определить реакции связей в функции угла a. Кроме того, необходимо найти значения угла a, при которых вес исследуемой опоры и потенциальная энергия деформации всех опор оказываются минимальными.
наклонена к оси x под углом a, который изменяется от 0 до 2p. Требуется определить реакции связей в функции угла a. Кроме того, необходимо найти значения угла a, при которых вес исследуемой опоры и потенциальная энергия деформации всех опор оказываются минимальными. , модуль которой равен модулю соответствующей силы реакции рассматриваемой опоры. Если реакцией опоры является пара сил, то паре соответствуют два стержня – по одному для каждой силы.
, модуль которой равен модулю соответствующей силы реакции рассматриваемой опоры. Если реакцией опоры является пара сил, то паре соответствуют два стержня – по одному для каждой силы. , (25)
, (25) , (26)
, (26)


















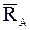 плоской системы сил реакций заделки, линия действия которой находится на некотором расстоянии h от точки A (h = MA/RA). В тех вариантах, где в точке A расположена шарнирно-неподвижная опора,
плоской системы сил реакций заделки, линия действия которой находится на некотором расстоянии h от точки A (h = MA/RA). В тех вариантах, где в точке A расположена шарнирно-неподвижная опора, .
.
 , где k = 1, 2,..., 24 и
, где k = 1, 2,..., 24 и  . По вычисленным значениям реакции RA строится график зависимости RA = RA (a), из которого находят значение a, соответствующее глобальному минимуму RA.
. По вычисленным значениям реакции RA строится график зависимости RA = RA (a), из которого находят значение a, соответствующее глобальному минимуму RA. , (27)
, (27) – удлинение (деформация) i -го стержня, вызванное силой N i.
– удлинение (деформация) i -го стержня, вызванное силой N i. . (28)
. (28) – длина i -го стержня;
– длина i -го стержня;  – площадь его поперечного сечения;
– площадь его поперечного сечения; 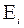 – модуль упругости материала, из которого этот стержень изготовлен.
– модуль упругости материала, из которого этот стержень изготовлен. , (29)
, (29) .
. считается известной и постоянной для всех стержней (
считается известной и постоянной для всех стержней ( ). Суммарная потенциальная энергия стержней (опор) найдется сложением (29):
). Суммарная потенциальная энергия стержней (опор) найдется сложением (29): . (30)
. (30) оптимизацию конструкции по потенциальной энергии деформации опор можно заменить оптимизацией по параметру, равному сумме квадратов модулей составляющих сил реакций всех опор. Соответствующая целевая функция будет
оптимизацию конструкции по потенциальной энергии деформации опор можно заменить оптимизацией по параметру, равному сумме квадратов модулей составляющих сил реакций всех опор. Соответствующая целевая функция будет , (31)
, (31) . Глобальный минимум этого графика соответствует оптимальному значению угла a.
. Глобальный минимум этого графика соответствует оптимальному значению угла a. , модуль которой Q = q×3 = 3 кН, а точка приложения находится на середине вертикального участка элемента СВ.
, модуль которой Q = q×3 = 3 кН, а точка приложения находится на середине вертикального участка элемента СВ.
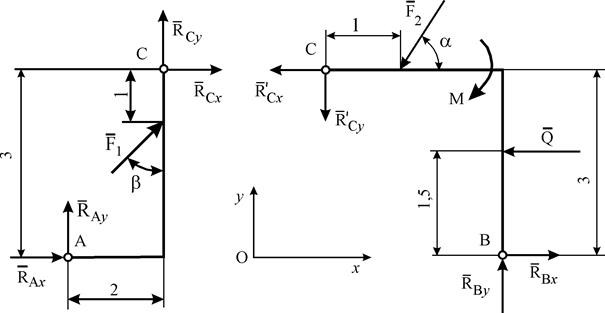
 и
и 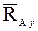 реакции
реакции 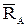 внешней связи, а в точке С – составляющие
внешней связи, а в точке С – составляющие  и
и  реакции
реакции  внутренней связи. В точке В элемента ВС прикладываем составляющие
внутренней связи. В точке В элемента ВС прикладываем составляющие  и
и  реакции
реакции  внешней связи, а в точке С – составляющие
внешней связи, а в точке С – составляющие  и
и  реакции
реакции 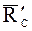 внутренней связи (
внутренней связи ( ).
).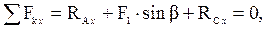 (32)
(32)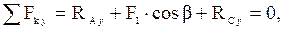 (33)
(33) (34)
(34) (35)
(35) (36)
(36) (37)
(37) , уравнения (32)–(37) перепишем в виде системы шести уравнений, перенеся в их правые части известные члены, считая, что значение угла a также задано:
, уравнения (32)–(37) перепишем в виде системы шести уравнений, перенеся в их правые части известные члены, считая, что значение угла a также задано: (38)
(38) ).
).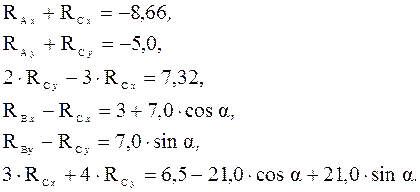 (39)
(39) (40)
(40) (41)
(41) (42)
(42) (43)
(43) (44)
(44) , где коэффициенты a, b и с зависят от заданных сил и их плеч.
, где коэффициенты a, b и с зависят от заданных сил и их плеч.
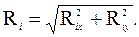
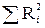

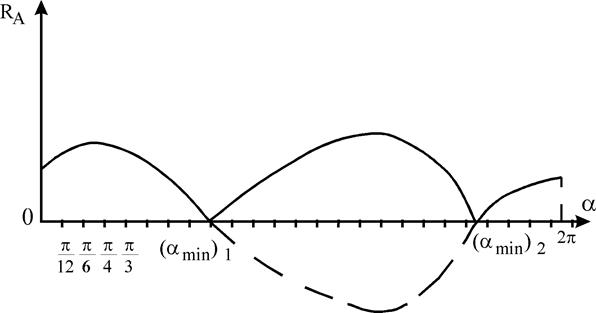






 точки, характеризующая быстроту и направление движения точки, равна производной по времени от ее радиуса-вектора:
точки, характеризующая быстроту и направление движения точки, равна производной по времени от ее радиуса-вектора: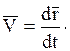
 точки, характеризующее изменение скорости по модулю и направлению, равно производной по времени от вектора скорости:
точки, характеризующее изменение скорости по модулю и направлению, равно производной по времени от вектора скорости:


 по координатным осям:
по координатным осям:



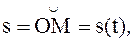


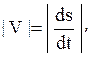







 , или
, или 
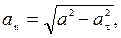

 , найдем радиус кривизны по формуле
, найдем радиус кривизны по формуле
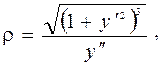
 и
и 


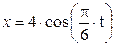




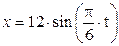
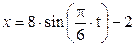



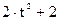








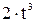


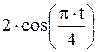






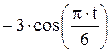
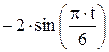









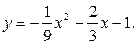









 м/с2.
м/с2. м/с2.
м/с2. м/с2.
м/с2. м.
м.
 строим по составляющим
строим по составляющим  и
и  ; он должен быть направлен по касательной к траектории. Вектор ускорения
; он должен быть направлен по касательной к траектории. Вектор ускорения  находим по его составляющим
находим по его составляющим  и
и  . Далее найденный вектор раскладываем на направления касательной и нормали и получаем векторы касательного
. Далее найденный вектор раскладываем на направления касательной и нормали и получаем векторы касательного  и нормального
и нормального  ускорений. Полученные таким образом значения
ускорений. Полученные таким образом значения 


