
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пространственная система силСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Момент силы относительно оси и его вычисление. Зависимость между моментом силы относительно центра и относительно оси, проходящей через этот центр. Аналитические формулы для вычисления моментов силы относительно трех координатных осей. Приведение пространственной системы сил к данному центру. Вычисление главного вектора и главного момента пространственной системы сил. Аналитические условия равновесия произвольной пространственной системы сил. Центр тяжести
Центр параллельных сил. Формулы для определения координат центра параллельных сил. Центр тяжести твердого тела; формулы для определения его координат. Центры тяжести объема, площади и линии. Способы определения положения центров тяжести тел. Центры тяжести дуги окружности, треугольника и кругового сектора.
Кинематика
Кинематика точки
Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Системы отсчета. Задачи кинематики. Векторный способ задания движения точки. Траектория точки. Скорость точки как производная ее радиуса-вектора по времени. Ускорение точки как производная от ее вектора скорости по времени. Координатный способ задания движения точки в прямоугольных декартовых координатах. Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси. Естественный способ задания движения точки. Естественный трехгранник и его оси. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника; касательное и нормальное ускорения точки. Выражение касательного ускорения точки через проекции скорости и ускорения на координатные оси. Поступательное движение твердого тела
Определение поступательного движения твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении.
Вращательное движение твердого тела вокруг неподвижной оси
Определение вращательного движения тела вокруг неподвижной оси. Уравнение (закон) вращательного движения твердого тела. Угловая скорость и угловое ускорение твердого тела. Законы равномерного и равнопеременного вращения. Скорость и ускорение точки тела, вращающегося вокруг неподвижной оси. Векторы угловой скорости и углового ускорения тела. Выражение скорости точки вращающегося тела и ее касательного и нормального ускорений в виде векторных произведений.
Плоскопараллельное (плоское) движение твердого тела
Плоское движение твердого тела и движение плоской фигуры в ее плоскости. Уравнения движения плоской фигуры. Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг полюса. Независимость угловой скорости и углового ускорения от выбора полюса. Теорема о скоростях точек плоской фигуры. Теорема о проекциях скоростей двух точек плоской фигуры. Мгновенный центр скоростей (МЦС) и доказательство его существования. Определение скоростей точек плоской фигуры с помощью МЦС. Теорема об ускорениях точек тела при плоском движении.
Вращательное движение твердого тела вокруг неподвижной точки (сферическое движение)
Углы Эйлера. Уравнения движения твердого тела вокруг неподвижной точки. Мгновенная ось вращения тела. Векторы угловой скорости и углового ускорения тела. Определение скорости и ускорения любой точки тела при его сферическом движении.
Свободное движение твердого тела
Уравнения движения свободного твердого тела. Разложение этого движения на поступательное движение вместе с полюсом и вращение вокруг полюса. Определение скоростей и ускорений точек свободного твердого тела. Составное (сложное) движение точки
Переносное, относительное и абсолютное движения точки. Скорости и ускорения точки в относительном, переносном и абсолютном движениях. Теорема о сложении скоростей. Теорема Кориолиса о сложении ускорений. Модуль и направление кориолисова ускорения (правило Н. Е. Жуковского). Случаи равенства нулю ускорения Кориолиса.
Составное движение твердого тела
Сложение поступательных движений. Сложение вращательных движений твердого тела вокруг параллельных и пересекающихся осей. Пара мгновенных вращений. Кинематический винт. Мгновенная винтовая ось.
Статика. Основные положения
Статикой называется раздел теоретической механики, в котором рассматриваются операции с силами и равновесие твердых тел. Под состоянием равновесия твердого тела понимают не только состояние покоя, но и движение по инерции. В основе теоретической механики лежат экспериментально установленные аксиомы (законы), справедливость которых проверена многовековой практической деятельностью человека. При действии сил на свободные тела их равновесие может быть нарушено. Тела или системы тел, равновесие которых изучается, несвободны, так как их перемещению в пространстве препятствуют другие (неподвижные) тела, скрепленные или соприкасающиеся с первыми. Тела, которые ограничивают (связывают) перемещение данного тела, называются связями. Сила, с которой данная связь действует на тело, препятствуя его перемещению, называется силой реакции связи или просто реакцией связи. Значения реакций связей определяются в процессе решения соответствующей задачи механики. Направлена же реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Ниже представлены наиболее часто встречающиеся типы связей и направления их реакций.
Рис. 1
Гладкая плоскость (поверхность или опора) (рис. 1). Реакция
Нить (канат, цепь, ремень, трос). Связь, осуществленная в виде гибкой нерастяжимой нити (рис. 2), не дает телу М удаляться от точки подвеса нити по направлению АМ. Поэтому реакция Неподвижный цилиндрический шарнир или подшипник (шарнирно-неподвижная опора). Цилиндрическим шарниром (рис. 3) называется совокупность неподвижной обоймы (втулки) 1 и помещенного в нее валика (пальца) 2, жестко соединенного с телом 3. В точке С соприкосновения втулки с валиком возникает сила опорной реакции, направленная по нормали к идеально гладким поверхностям. Эта нормаль проходит через геометрический центр А валика. Так как положение точки С соприкосновения валика со втулкой заранее не известно, то невозможно сразу указать направление силы реакции
Шарнирно-подвижная опора (опора на катках). Реакция
Сферический шарнир (рис. 6). Сферическим шарниром называется устройство, выполненное в виде двух контактирующих сфер, геометрический центр А которых неподвижен. Тело 3, равновесие которого рассматривается, жестко связано с внутренней подвижной сферой 1. При условии, что сферические поверхности гладкие, реакция Подпятник (рис. 7). Подпятник представляет собой соединение цилиндри-ческого шарнира 2 и опорной плоскости 3, на которую опирается вал 1. Реакция подшипника, лежащая в плоскости перпен-дикулярной оси вала, представляется двумя ее взаимно-перпендикулярными составляющими Невесомый стержень (рис. 8). Реакция
Рис. 8 Жесткая заделка (неподвижное защемление) конца балки (рис. 9). Такая связь не допускает не только линейных перемещений балки 1 вдоль координатных осей, но и вращения балки в плоскости х А у.
Рис. 9
Нахождение реакций жесткой заделки сводится к определению трех неизвестных величин: составляющих Для того чтобы составить уравнения равновесия, надо уметь вычислять проекции сил на координатные оси и выполнять операции сложения и разложения сил. Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Так, для сил, изображенных на рис. 10:
F x = a 1 b 1 = Fcos a;F у = a2b2 = F cos (90° - a) = F sin a; Q x = c 1 d 1 = Q cos b = Q cos (180° + g) = - Q cosg; Q у = c 2 d 2 = Q cos (90° + g) = - Q sin g.
Проекцией силы
Рис. 10
По модулю F ху = F cos q, где q - угол между направлением силы В некоторых случаях для нахождения проекции силы на ось удобнее сначала найти ее проекцию на плоскость, в которой расположена эта ось, а затем полученный вектор спроецировать на данную ось. Например, в случае, изображенном на рис. 11, найдем:
F х = ОВ2 = F ху cos j = F cos q×cosj, F у = ОВ3 = F ху sin j = F cos q×sin j.
Рис. 11 Геометрическое сложение сил
Рис. 12
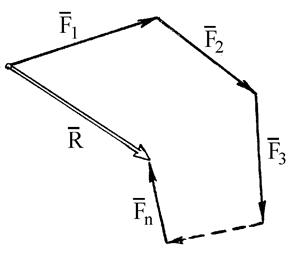
Аналитическое сложение сил основано на известной теореме векторной алгебры: проекция вектора суммы на ось равна алгебраической сумме проекций слагаемых векторов на ту же ось:
Модуль (численное значение) главного вектора
Действие силы на твердое тело может вызвать вращательный эффект, который для плоской системы сил оценивается моментом силы относительно какой-либо точки О на плоскости (рис. 13):
где h1 и h2 - плечи сил
Рис. 13
Плечом называется длина перпендикуляра, опущенного из точки О на линию действия соответствующей силы. Если данная сила стремится вращать тело вокруг точки О против хода часовой стрелки, то ее моменту относительно этой точки приписывают знак «+». Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю (например, Вычисление момента силы относительно какой-либо точки во многих случаях упрощается, если эту силу разложить на две взаимно-перпендикулярные составляющие и применить теорему Вариньона, согласно которой момент равнодействующей сходящихся сил относительно любого центра равен сумме моментов составляющих сил относительно того же центра. Например, для равнодействующей силы
где
Таким образом,
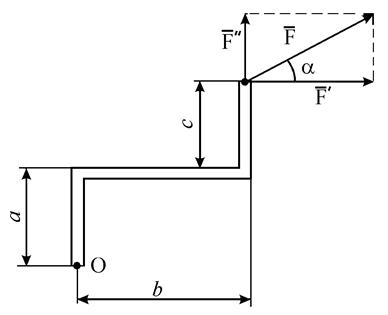
Вращательный эффект вызывает также пара сил, под которой понимается совокупность двух сил, равных по модулю, направленных в противоположные стороны и линии действия которых параллельны (рис. 15).
Рис. 14
Пара сил, стремящаяся вращать тело против хода часовой стрелки, считается положительной, а по ходу часовой стрелки - отрицательной. Пара сил характеризуется ее моментом, который равен взятому со знаком «плюс» или «минус» произведению модуля одной из сил данной пары на плечо пары, т. е. на кратчайшее расстояние между линиями действия сил пары.
Рис. 15
Обозначив момент пары буквой m, а плечо пары буквой d, будем иметь (рис. 15):
m1 = F1 × d1; m2 = -F2 × d2. Систему пар сил, расположенных в одной плоскости, можно заменить одной эквивалентной парой, момент которой М равен алгебраической сумме моментов пар:
М = m1 + m2 +... +mn =
|
|||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

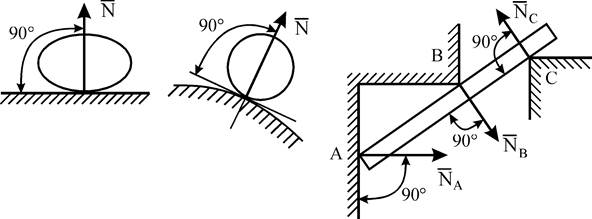
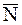 гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке.
гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке.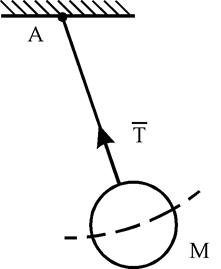 Рис. 2
Рис. 2
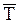 натянутой нити направлена вдоль нее от тела к точке подвеса.
натянутой нити направлена вдоль нее от тела к точке подвеса.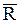 , но можно утверждать, что линия действия реакции
, но можно утверждать, что линия действия реакции 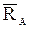 при решении задач представляют в виде двух ее взаимно-перпендикулярных составляющих
при решении задач представляют в виде двух ее взаимно-перпендикулярных составляющих 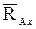 и
и 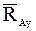 . После определения их значений находят значение реакции
. После определения их значений находят значение реакции 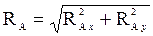 ,
, 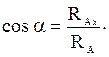
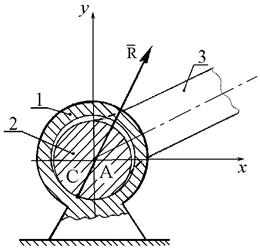
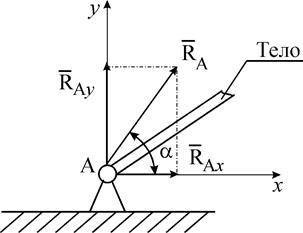 Рис. 3 Рис. 4
Рис. 3 Рис. 4
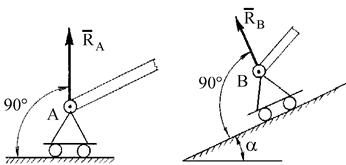 Рис. 5
Рис. 5
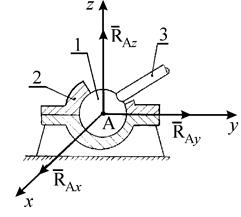 Рис. 6
Рис. 6
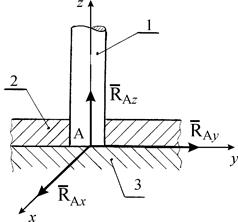 Рис. 7
Рис. 7
 ,
, 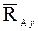 и
и 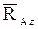 , направленных вдоль координатных осей.
, направленных вдоль координатных осей.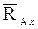 и
и 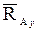 , а реакция опорной плоскости - реакцией
, а реакция опорной плоскости - реакцией 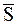 прямолинейного невесомого (идеального) стержня направлена вдоль этого стержня. Если связью является криволинейный стержень, то реакция направлена вдоль прямой АВ, соединяющей концевые шарниры А и В.
прямолинейного невесомого (идеального) стержня направлена вдоль этого стержня. Если связью является криволинейный стержень, то реакция направлена вдоль прямой АВ, соединяющей концевые шарниры А и В.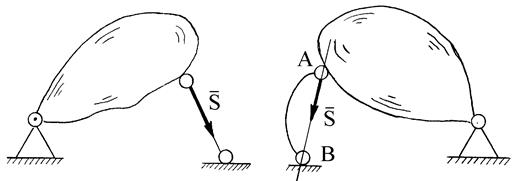
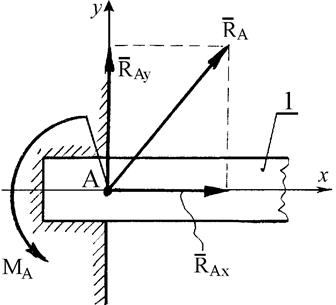
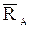 и так называемого реактивного момента МА, препятствующего вращению балки в плоскости х А у вокруг точки А.
и так называемого реактивного момента МА, препятствующего вращению балки в плоскости х А у вокруг точки А.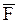 на плоскость О ху называется вектор
на плоскость О ху называется вектор 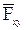 =
= 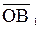 , заключенный между проекциями начала и конца силы
, заключенный между проекциями начала и конца силы 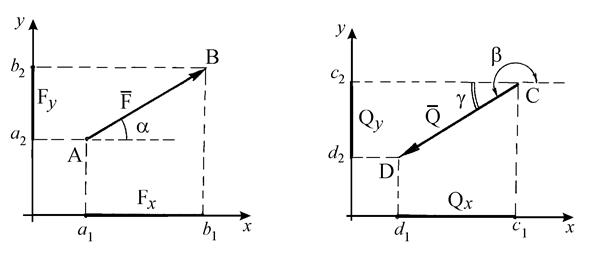
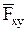 .
.
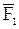 ,
, 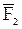 ,...,
,..., 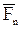 основывается на построении в масштабе векторного многоугольника, замыкающая сторона которого представляет эту сумму и называется главным вектором
основывается на построении в масштабе векторного многоугольника, замыкающая сторона которого представляет эту сумму и называется главным вектором 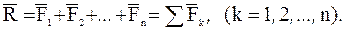
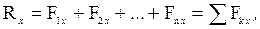
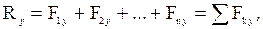
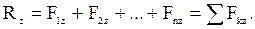
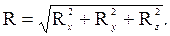
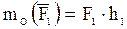 ;
;  ,
,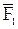 и
и 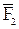 относительно точки О.
относительно точки О.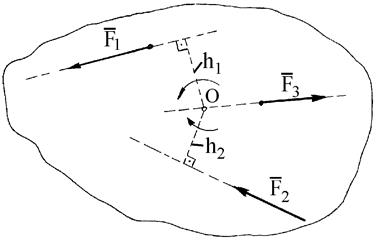
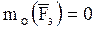 ).
).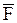 и ее составляющих
и ее составляющих 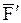 и
и 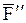 (рис. 14) имеем:
(рис. 14) имеем: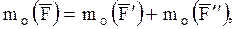


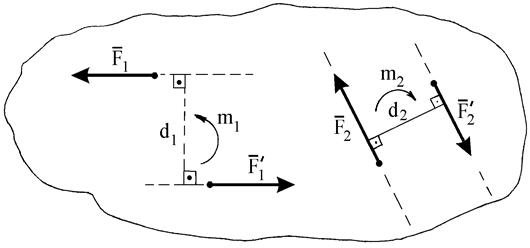
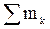 (k = 1, 2,..., n).
(k = 1, 2,..., n).


