Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематический расчет манипулятораСодержание книги Поиск на нашем сайте
Рассмотрим вращательное движение твердого тела вокруг неподвижной оси Оz (рис. 30). Выделим какую-либо точку М этого тела. Как известно [2], вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки, т. е.
Модуль скорости точки М равен модулю векторного произведения
где h – расстояние от оси вращения до точки М. Рассматривая вращение стержня ОА (рис. 31) вокруг оси, проходящей через точку О перпендикулярно к плоскости рисунка, и полагая, что вектор угловой скорости
В формуле (73) стержень ОА представлен в виде вектора
Проецируя векторное равенство (73) на координатные оси, получаем проекции
Формулы (74) и (75) будут справедливы для любых значений угла j, если отсчет этого угла производить против хода часовой стрелки от положительного направления оси Ох до направления вектора В случае плоскопараллельного (плоского) движения твердого тела скорость какой-либо точки В (рис. 32) равна геометрической сумме скорости точки А, принятой за полюс, и скорости точки В при вращении тела вокруг полюса А, т. е.
где
С учетом последнего выражения формула (76) приобретет вид
Проецируя равенство (77) на координатные оси, получаем формулы для определения проекций скорости точки В на эти оси:
Плоские механизмы в своем составе могут содержать звенья (тела), совершающие вращательное движение вокруг неподвижных осей, и звенья, совершающие плоское движение. При определении скоростей отдельных точек таких звеньев будем применять формулы, аналогичные формулам (73)–(79).
Задача К4
На с. 97-101 приведены схемы манипуляторов для различных вариантов задания. Здесь же даны соотношения между длинами звеньев. Необходимые исходные данные приведены в табл. К4.1. В вариантах К4.4, К4.9, К4.15, К4.17, К4.22 и К4.25 каток 2 относительно опорной поверхности не проскальзывает. Закон изменения скорости схвата груза А для всех вариантов задания одинаков и имеет вид
VA = VAy = V×sin pt; V = 0,45 м/с; р = 1,87 рад/с.
Кинематический расчет манипулятора необходимо провести в интервале времени t = 0-1,68 с шагом 0,07 с. Пример К4. Рассмотрим манипулятор, предназначенный для перемещения груза А (рис. К4а). Груз за отрезок времени t под действием двигателей управления, расположенных в шарнирах В и D, перемещается по вертикальной прямой из точки а в точку b с заданной скоростью
Рис. К4а
Звенья манипулятора считаются абсолютно твердыми телами. Каток 2 относительно опорной поверхности не проскальзывает. Требуется определить угловые скорости w1, w2, w3 звеньев 1, 2, 3, а также скорость точки С как функции времени. Схемы манипуляторов
Таблица К4.1
Размеры звеньев: АВ = r1 = 0,7 м, BD = r2 = 0,5 м, DC = r3 = 0,8 м, значения углов, определяющих положения звеньев манипулятора в начальный момент времени (t = 0): j1 (0) = 0,5 рад; j2 (0) = 0,3 рад; j3 (0) = 1,0 рад. Порядок расчета. Исходные соотношения для расчета получим, воспользовавшись векторным описанием геометрии механизма, расчленив его на две группы звеньев (рис. К4б и рис. К4в).
Рис. К4б
Рис. К4в
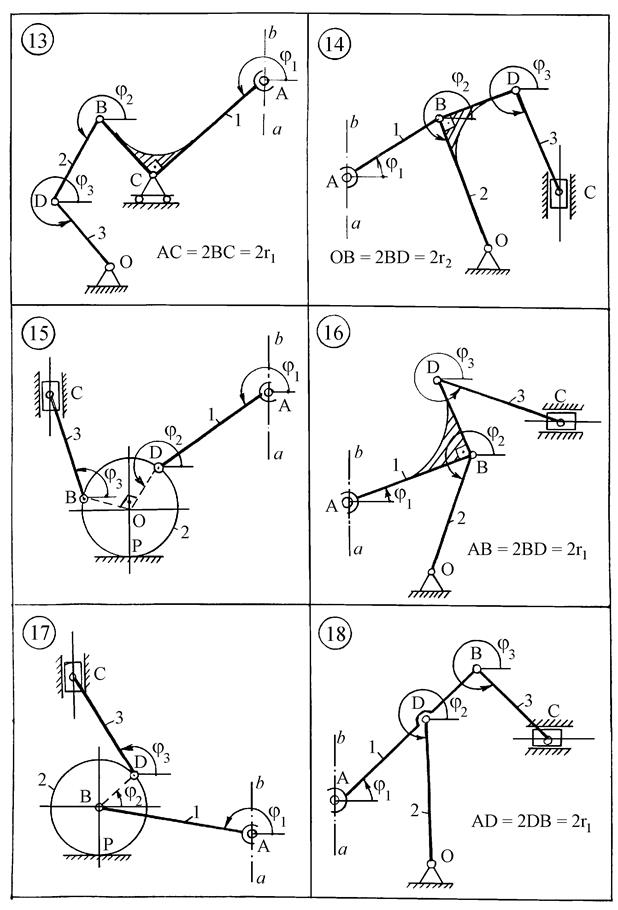
Из рис. К4б следует
Входящие сюда векторы Продифференцировав равенство (80) по времени, получим
где обозначение
где С учетом (82) равенство (81) будет иметь вид
Спроецировав векторное равенство (83) на координатные оси и учитывая, что АВ = r1, BD = DP = r2, получим два скалярных уравнения:
Так как точка Р, принадлежащая катку 2, является мгновенным центром скоростей, то VPx = VPy = 0. Кроме того, sin (3p/2) = –1, cos (3p/2) = 0 и, как следует из условий задачи, VAx = 0 и VАy = VA = V×sin pt. С учетом этих замечаний уравнения (84) и (85) принимают вид:
w1 × r1 sin j1 + w2 × r2 (sin j2 - 1) = 0, (86)
w1 × r1 cos j1 + w2 × r2 × cos j2 + V× sin pt = 0. (87)
Рис. К4в позволяет составить следующее векторное равенство:
после дифференцирования которого по времени получим
или
Спроецировав векторное равенство (88) на координатные оси и учитывая, что PD = r2 и DC = r3, находим:
VCx = VPx – w2 × r2 × sin(p/2) – w3 × r3 × sin j3,
VCy = VPy + w2 × r2 × cos(p/2) + w3 × r3 × cos j3.
В этих уравнениях VCx = 0, VPx = VPy = 0, VCy = VC, sin (p/2) = 1, сos (p/2) = 0. С учетом этих замечаний последние уравнения приобретают вид:
w2 × r2 + w3 × r3 sin j3 = 0, (89)
w3 × r3 cos j3 - VC = 0. (90)
Полученная система четырех линейных уравнений (86), (87), (89) и (90) позволяет определить четыре неизвестных w1, w2, w3 и VC. Подставив в эти уравнения числовые значения заданных величин, получим систему уравнений:
0,7 × sin j1 × w1 + 0,5 (sin j2 - 1)× w2 = 0,
0,7 × cos j1 × w1 + 0,5 cos j2 × w2 + 0,45 × sin (1,87×t) = 0, (91) 0,5 × w2 + 0,8 sin j3 × w3 = 0,
0,8 cos j3 × w3 - VC = 0.
Для проведения расчетов по формулам (91) с помощью универсальной математической системы MathCAD приведем эти уравнения к стандартной матричной форме:
A(j1, j2, j3) × X(t, j1, j2, j3) = B(t), (92)
где A(j1, j2, j3) – матрица коэффициентов при w1, w2, w3 и VC; B(t) – матрица свободных членов; X(t, j1, j2, j3) – матрица-столбец неизвестных. Расположим элементы матрицы столбца X(t, j1, j2, j3) в следующем порядке:
В этом случае матрица A(j1, j2, j3) и столбец свободных членов B(t) таковы:
Выражение (92) можно записать как
Принимая во внимание, что
из (93) получаем систему дифференциальных уравнений вида
Для решения полученных уравнений используем функцию rkfixed(f 0, t0, t, n, D), возвращающую матрицу решений методом Рунге-Кутта. Задаем решение уравнений
z = rkfixed(f 0, t0, t, n, D),
где f 0 – вектор начальных условий для углов j1(0), j2(0), j3(0); t0 – начальный момент времени; t – конечный момент времени; n – число шагов; D – вектор правых частей дифференциальных уравнений (95). В результате расчетов получим: Введя вспомогательные функции
определим векторы значений:
Ниже приведена программа расчета, а результаты решения по изложенному методу содержатся в табл. К4.2 и на рис. К4г.
Таблица К4.2 Результаты решения задачи
Рис. К4г
Для составления программ на языке Pascal уравнения (91) представим в явном виде относительно w1, w2, w3 и VC:
(96)
Конечно-разностная схема Эйлера для уравнений (94), (96) приводит к следующим уравнениям, связывающим значения углов и угловых скоростей в начале и конце k-го шага интегрирования:
j1 (k + 1) = j1 (k) + w1(k) × Dt,
j2 (k + 1) = j2 (k) + w2(k) × Dt,
j3 (k + 1) = j3 (k) + w3(k) × Dt.
Учитывая начальные условия j1(0), j2(0), j3(0) и шаг по времени Dt, организуем цикл по времени с помощью стандартного оператора
repeat ...... Тело цикла (формулы (96) для вычислений w1, w2, w3 и VC) ..... until t > t.
На печать с шагом Dt = t/24 = 0,07 c выводятся переменные t, j1, j2, j3, w1, w2, w3 и VC. Ниже представлена программа и результаты расчета на языке Pascal (табл. К4.3), а также график изменения скоростей в зависимости от времени (рис. К4д).
Program Mаnipul const dt=1.68/24;
Var om1, om2, om3, Vc, f1, f2, f3, t, K1, K2: REAL; F, S: Text;
Begin t:= 0; f1:= 0.5; f2:= 0.3; f3:= 1.0; Assign(F, 'S41.dat'); Assign(S, 'S42.dat'); ReWrite(F); ReWrite(S); Repeat K1:= sin(f1)*cos(f2) - cos(f1)*(sin(f2) - 1); om1:= 0.6428*sin(1.87*t)*(sin(f2) - 1)/K1; K2:= - K1; om2:= 0.9*sin(1.87*t)*sin(f1)/K2; om3:= 0.5625*sin(1.87*t)*sin(f1)/(K1*sin(f3)); Vc:= 0.45*sin(1.87*t)*sin(f1)*cos(f3)/(K1*sin(f3)); Writeln(F, t:8:3, f1:8:3, f2:8:3, f3:8:3, om1:10:4, om2:10:4, om3:10:4, Vc:10:4); Writeln(S, t:8:3, om1:8:3, om2:10:3, om3:10:3, Vc:12:3); t:= t + dt; f1:= f1 + om1*dt; f2:= f2 + om2*dt; f3:= f3 + om3*dt; Until t >= 1.68 + 0.15;
End.
Таблица К4.3 Результаты расчета
Рис. К4д
Оценим полученные результаты, сравнив их со значениями скоростей, вычисленными для какого-либо момента времени с помощью мгновенных центров скоростей. Например, при t = 0,7 с из табл. K4.2 имеем: j1 = 0,339 рад = 19,42°, j2 = 0,167 рад = 10,08°, j3 = 1,09 рад = 62,45°, VA = 0,435 м/с. Вычертим в масштабе схему механизма для выписанных углов (рис. К4е) и покажем на ней положение мгновенных центров скоростей.
Рис. К4е
Угловая скорость звена 1
Скорость точки В
VB = w1 BP1 = 0,4627×0,37 = 0,1712 м/с.
Угловая скорость колеса (звена 2)
Скорость точки D
VD = w2 DP2 = 0,2634×0,5 = 0,1371 м/с.
Угловая скорость звена 3
Скорость точки С
VC = w3 CP3 = 0,1829×0,38 = 0,0695 м/с.
Полученные результаты практически совпадают с результатами расчета на ЭВМ.
Библиографический список
1. Бутенин, Н. В. Курс теоретической механики: В 2 т. / Н. В. Бутенин, Я. Л. Лунц, Д. Р. Меркин. СПб.: Изд-во «Лань», 1998. 736 с. 2. Тарг, С. М. Краткий курс теоретической механики: Учеб. для втузов / С. М. Тарг. М.: Высш. шк, 1995. 416 с. 3. Яблонский, А. А. Курс теоретической механики / А. А. Яблонский, В. М. Никифорова. М.; СПб.: Изд-во «Лань», 2001. 768 с. 4. Бать, М. И. Теоретическая механика в примерах и задачах. Статика и кинематика: Учеб. пособие / М. И. Бать, Г. Ю. Джанелидзе, А. С. Кельзон. СПб: Политехника, 1995. 670 с. 5. Новожилов, И. В. Типовые расчеты по теоретической механике на базе ЭВМ. / И. В. Новожилов, М. Ф. Зацепин. М.: Высш. шк., 1986. 136 с. 6. Мартынов, А. Г. Определение опорных реакций составной балки с элементами оптимизации: Метод. указания / Сост. А. Г. Мартынов, Т. П. Мартынова. Красноярск: КГТУ, 1997. 20 с. 7. Мартынов, А. Г. Кинематический расчет манипулятора: Метод. указания / Сост. А. Г. Мартынов, К. А. Редкоус. Красноярск: ИПЦ КГТУ, 2000. 26 с.
Оглавление
Введение 3 Программа курса «Теоретическая механика» 3 1. Статика. Основные положения 6 1.1. Произвольная плоская система сил 15 Задача С1 17 Задача С2 22 1.2. Система сходящихся сил 29 Задача С3 29 1.3. Произвольная пространственная система сил 34 Задача С4 39 1.4. Определение опорных реакций составной балки с элементами оптимизации 44 Задача С5 44 Пример выполнения задания 51 2. Кинематика 61 2.1. Кинематика точки 61 Задача К1 64 2.2. Кинематика плоскопараллельного движения твердого тела 69 Задача К2 74 2.3. Составное (сложное) движение точки 82 Задача К3 85 2.4. Кинематический расчет манипулятора 94 Задача К4 96 Библиографический список 116
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.164 (0.013 с.) |


 (72)
(72) :
:
 направлен вдоль этой оси (к нам), применим формулу (72) для нахождения скорости точки А:
направлен вдоль этой оси (к нам), применим формулу (72) для нахождения скорости точки А: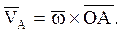 (73)
(73)
 . Направление этого вектора определим углом
. Направление этого вектора определим углом  , отсчитанным от положительного направления оси Ох против хода часовой стрелки. Отметим, что модуль вектора
, отсчитанным от положительного направления оси Ох против хода часовой стрелки. Отметим, что модуль вектора 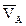 перпендикулярен этому стержню. Угол между вектором
перпендикулярен этому стержню. Угол между вектором 
 (74)
(74) (75)
(75)
 (76)
(76) определяется по формуле, аналогичной формуле (73):
определяется по формуле, аналогичной формуле (73):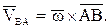
 (77)
(77) (78)
(78) (79)
(79) (
( ), являющейся известной функцией времени.
), являющейся известной функцией времени.






 (80)
(80) и
и  определяют положение точек А и Р относительно неподвижного начала О1 системы координат хО1у. Векторы, обозначенные двумя буквами, задают положение точки, определяемой второй из этих букв, относительно точки, обозначенной первой буквой.
определяют положение точек А и Р относительно неподвижного начала О1 системы координат хО1у. Векторы, обозначенные двумя буквами, задают положение точки, определяемой второй из этих букв, относительно точки, обозначенной первой буквой. (81)
(81) с одним индексом (Р или А) соответствует значению абсолютной скорости точки Р или А, а обозначение
с одним индексом (Р или А) соответствует значению абсолютной скорости точки Р или А, а обозначение 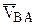 есть скорость точки в во вращательном движении звена АВ вокруг точки А. Указанные скорости определяются известными соотношениями:
есть скорость точки в во вращательном движении звена АВ вокруг точки А. Указанные скорости определяются известными соотношениями:

 (82)
(82) ,
,  – векторы угловых скоростей звеньев 1 и 2, направленные перпендикулярно чертежу.
– векторы угловых скоростей звеньев 1 и 2, направленные перпендикулярно чертежу. (83)
(83) (84)
(84)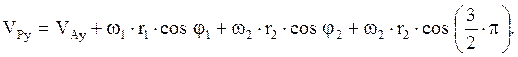 (85)
(85)

 (88)
(88)


 (93)
(93)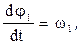

 (94)
(94) (95)
(95) – вектор значений времени;
– вектор значений времени;  – вектор значений j1;
– вектор значений j1; 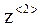 – вектор значений j2;
– вектор значений j2;  – вектор значений j3 для каждого шага времени n.
– вектор значений j3 для каждого шага времени n. ,
, ,
, ,
, ,
,