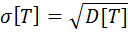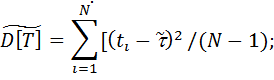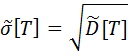Показатели надежности невосстанавливаемых систем.

 

При выборе показателей надежности следует иметь в виду, что эти показатели должны достаточно полно описывать надежностные свойства системы, быть удобными для аналитического расчета и экспериментальной проверки по результатам испытаний, должны иметь разумный физический смысл и, наконец, допускать возможность перехода к показателям эффективности.

Для невосстанавливаемых систем можно ограничиться показателями безотказности. Безотказность невосстанавливаемых технических систем является наиболее важной компонентой надежности систем, так как она отражает их способность длительное время функционировать без отказов.

Эта способность системы в решающей степени влияет на ее эффективность и определяется количеством и безотказностью элементов, режимом их работы, наличием резервирования, параметрами окружающей среды (температура, влажность, атмосферное давление и т. д.).

Показатели безотказности описывают системы, в принципе подлежащие восстановлению после отказов, но поведение, которых целесообразно рассматривать до момента первого отказа. К их числу, например можно относить системы, чьи отказы чрезвычайно редки и вызывают особо тяжелые последствия.

Функция и плотность распределения наработки до отказа. Наработка до отказа обозначается символом Т, как и любая иная случайная величина, описывается функцией распределения F(t), определяемой как вероятность Р (вероятность безотказной работы) случайного события, заключающегося в том, что наработка до отказа Т меньше некоторой заданной наработки t (время).

 

F(t)=P{T<t} (2.1)

Эта вероятность рассматривается как функция t во всем диапазоне возможных значений величины Т.

Функция распределения любой случайной величины неубывающей функцией времени t. При величина t→∞ величина F(t) стремится к единице.

Рисунок 2.2 – Примерный вид функции распределения F(t) и функции надежности P(t)

 

Кроме указанного (2.1) вероятностного определения функции F(t), для всех показателей надежности можно привести и статистические определения, используемых при испытаниях на надежность. Статистические определения позволяют более полно обяснять смысл вероятностных определений. Далее статистические определения будем обозначать волнистой чертой.

Для рассмотрения статистических определений показателей надежности невосстанавливаемых систем предположим, что на испытание поставлено одинаковых систем, условия испытаний одинаковы, а испытания каждой из систем производятся до ее отказа. Обозначим N(t) число систем, отказавших к моменту времени t, т.е. на интервале (0,t). Очевидно, что N(0)=0, а при t→∞ величина N(t) →N.

Статистическим определением функции распределения F(t) является функция:

~ ~

F(t)=N(t)/N (2.2)

График статистической функции распределения F(t) представляет собой ступенчатую линию со скачками кратными 1/N в моменты отказов (рисунок 2.2). С ростом количества испутуемых систем N статистическая функция распределения сравнивается с вероятностной.

Исправная работа технической системы и ее отказ в течение времени t являются несовместимыми противоположными событиями, поэтому введем еще одну функцию:

 

P(t)=P{T>=t}=1-F(t) (2.3),

 

которую называют функцией надежности. Так при =0 система работоспособна, то Р(0)=1. С увеличением времени монотонно убывает, а при величина Р() 0. Примерный вид функции надежности приведен на рисунке 2.2.

Статистическое определение функции надежности:

~ ~

P(t)= 1-F(t)=[N-N(t)] / N (2.4)

 

где N-N(t) – число систем работоспособных к моменту времени t. Функция распределения F(t), как правило, непрерывна, и существует непрерывная плотность распределения наработки до отказа, вероятностное определение которой:

f(t)=dF(t)/dt (2.5)

 

Для статистического определения рассмотрим интервал времени (t-Dt/2,t+Dt/2), где Dt- длина этого интервала. Тогда статистическое определение плотности распределения

 

∼ N(t+Dt/2)-N(t-Dt/2) N(t-Dt/2, t+Dt/2)

f(t)= ------------------------- = ------------------- (2.6)

N*Dt N*Dt

 

Если в формуле 2.1 и 2.2 зафиксировать время = t1, тогда вероятность отказа и безотказной работы имеет следующее вероятностное определение:

Q(t1)=F(t1)=P{T<t1};

P(t1) = P{T>=t1}

 

Статистическое определение:

~

Q(t1)=N(t1)/N;

~ ~

P(t1) = 1-Q(t1) = [N-N(t1)] / N

 

Для решения различных задач в качестве показателя надежности используется вероятность безотказной работы Р(t1, t2) системы на интервале (t1, t2) при условии, что система безотказно проработала до момента t1. Вероятность события АВ – безотказной работы на интервале (0, t2) будет:

P{AB}=P{A}*P{B/A}

Отсюда

P(t1,t2) =P{B/A}=P{AB}/P{A} = P(t2)/P(t1) (2.7)

 

При описании надежности невосстанавливаемых систем широкое применение получила такая характеристика, как интенсивность отказов.

Интенсивность отказов – определяется как условная плотность вероятности отказа системы в момент времени t при условии, что до этого момента не возникали.

Выражает собой отношение числа отказавших объектов в единицу времени к среднему числу объектов, исправно работающих в данный отрезок времени при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными. Условная вероятность безотказной работы системы на интервале при условии, что система работоспособна в момент времени, определяется выражением (2.7)

 

P(t,t+ D t) = 1- P(t+ D t)/P(t) = -[ P(t+ D t)-P(t)]/P(t)

 

Устремив время к нулю, получим вероятностное значение интенсивности отказов:

l =lim (2.8)

 

Статистическое определение интенсивности отказов:

(2.9)

Интенсивность отказов l(t) дает наглядную картину изменения безотказности. Типичная зависимость во времени дана на рисунке 2.3. В период приработки выявляются скрытые дефекты изготовления отдельных элементов системы, недостатки монтажа, наладки, нарушения, произошедшие в результате транспортировки. Период эксплуатации характеризуется относительно постоянным показателем интенсивности отказов. В период старения системы из-за износа отдельных элементов и изменения их характеристик интенсивность отказов возрастает.

t

l(t)

 

Рисунок 2.3 – Типичный график изменения интенсивности отказов

 

Для решения значительного числа задач надежности технических систем достаточно знать только показатели, являющиеся числовыми характеристиками этой случайной величины. К ним относится в первую очередь относится средняя наработка до отказа (среднее время безотказной работы системы) – математическое ожидание (М[T]) случайной величины Т – наработки системы (объектов) до первого отказа.

¥

t = М[T]= ò t* f(t)dt; (2.10)

¥

t = ò P(t)dt; (2.11)

Из уравнения (2.11) следует, средняя наработка до отказа геометрически равна площади под кривой P(t) (рисунок 2.2). Статистическое определение наработки до отказа:

; (2.12)

 

Показатель Т важен в первую очередь для сложных систем с большим числом элементов.

Дисперсия и среднеквадратическое отклонение наработки до отказа:

 

 

Рассмотренные показатели применяются как при создании системы, так и при ее эксплуатации.

С помощью выбранного метода, исходя из структурной схемы системы, определяют аналитические модели, связывающие ее показатели с характеристиками элементов и процессов их обслуживания.

Подбор характеристик надежности элементов структурной схемы сопряжен с трудностями, определяемыми рядом факторов. К их числу относится зависимость показателей надежности от условий эксплуатации, которые могут существенно различаться на разных видах производств, поэтому паспортные данные по надежности могут не совпадать с их фактическими значениями.

Используя показатели надежности элементов невосстанавливаемых систем, по полученным математическим моделям производят расчет показателей надежность, который может быть выполнен с использованием соответствующих пакетов прикладных программ.