
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимость надежности от времениСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из рассмотренных выше выражений для оценки количественных характеристик надежности видно, что все характеристики, кроме средней наработки до первого отказа являются функциями времени. Время между соседними отказами для элементов аппаратуры является непрерывной случайной величиной, которая характеризуется некоторым законом распределения. Зависимость надежности от времени описывается с помощью математической модели надежности (ММН) – математического выражения (формулы, алгоритма, уравнения, системы уравнений), позволяющего определить показатели надежности. Простейшие ММН в виде формул носят название статистических моделей распределения. При исследовании надежности применяются следующие модели распределения: экспоненциальный, нормальный, Рэлея, Пуассона, Вейбулла и др. [1, 2, 3, 8]. Наиболее распространенной статистической моделью надежности является экспоненциальная модель распределения времени до отказа, по которой вероятность безотказной работы объекта выражается зависимостью
где λ – параметр модели. Частота отказа при экспоненциальной модели
аэ (t) = -dP (t) /dt = λ∙e-λ∙t. (8)
Функция интенсивности отказов при экспоненциальной модели λэ (t) = аэ (t) /Рэ (t) = λ = const. (9)
Графики этих функций приведены на рис. 1.
Рис. 1. График зависимости показателей надежности от времени для экспоненциальной модели распределения.
Наработка до отказа при экспоненциальной модели
Экспоненциальная модель может быть использована в случае, когда интенсивность отказов постоянная величина (λ=const), а также как характеристика достаточна сложных восстанавливаемых объектов в период эксплуатации II, если исключить период приработки I и период интенсивного старения III (рис. 1). С экспоненциальной моделью тесно связана модель Пуассона. Она основана на представлении о потоке случайных событий, называемого пуассоновским, если выполнены условия стационарности, ординарности и отсутствия последействия. Стационарность – свойство потока, выражающееся в том, что параметры потока не зависят от времени. Ординарность – свойство потока, выражающееся в том, что в один и тот же момент времени может произойти только одно событие. Отсутствие последействия – свойство потока, выражающееся в том, что вероятность наступления данного события не зависит от того, когда произошли предыдущие события и сколько их было. Таким образом модель Пуассона позволяет выразить вероятность Р (t, n) того, что на заданном интервале времени произошло равно n событий (отказов), если время между отдельными событиями (отказами) распределено экспоненциально с параметром λ. По модели Пуассона
Модель Вейбулла находит практическое применение благодаря своей простоте и гибкости, так как в зависимости от значений параметров характер модели видоизменяется в широких пределах. Модель надежности Вейбулла, называемая также моделью Вейбулла-Гнеденко, была предложена шведским ученым В. Вейбуллом в качестве модели прочности материалов, а затем обоснована математически российским ученым Б.В. Гнеденко. Вероятность безотказной работы по модели надежности Вейбулла выражается формулой [1, 8].
где α и β – параметры модели. Ориентировочно значение β=0,2÷0,4 для электронных устройств с убывающей функцией интенсивности отказов и β=1,2÷1,4 для механических устройств и возрастающей функцией интенсивности отказов.
Пример прогнозирования вероятности безотказной работы КС. Пусть вероятность безотказной работы КС за t =1000 ч. равна Р=0,99, составим прогноз вероятности безотказной работы этой же КС через 105 ч. работы без обслуживания. В случае экспоненциальной модели интенсивность отказов КС
В случае модели Вейбулла при β=0,5
Следовательно, через 105 ч работы вероятность безотказной работы КС, прогнозированной по экспоненциальной модели, равна
Прогноз по модели Вейбулла
Следовательно, выбор правильной модели надежности не безразличен для практики. Нормальное распределение и модель Рэлея используют для описания таких систем и устройств, которые подвержены действию износа, здесь величина интенсивности λ (t) монотонно возрастает. Выбор модели надежности – сложная научно-техническая проблема. Она может быть удовлетворительно решена стандартными методами математической статистики, если имеется большой статистический материал об отказах исследуемых объектов. Из-за высокой надежности КС и их компонентов, как правило, статистических данных об отказах немного. В последнем случае при выборе модели руководствуются результатами ускоренных испытаний, проводимыми в утяжеленных условиях работы объекта, физическими соображениями, предыдущим опытом. В случае приближенных оценок часто выбирается экспоненциальная модель как наиболее удобная с точки зрения аналитических преобразований. Экспоненциальную модель рекомендуется применить при выполнении расчетов надежности в случае отсутствия других исходных данных для расчета, кроме интенсивности отказов. В случае наличия более полных исходных данных целесообразно пользоваться другой, более точной моделью, например моделью Вейбулла.
Контрольные вопросы и задания
1. Что характеризует коэффициент готовности системы? 2. В каких случаях целесообразно выбрать в качестве показателя надежности вероятность безотказной работы; наработку до отказа; наработку на отказ? 3. Каким соотношением связаны коэффициент готовности компьютерного устройства – Кг и коэффициент простоя – Кп? 4. Какой показатель ремонтопригодности характеризующий надежность объекта, рекомендуется использовать, если важное значение имеет безотказная работа? 5. Какую формулу необходимо использовать при расчете коэффициента простоя? 6. Дайте определение коэффициента готовности системы. 7. Что такое поток отказов? 8. Назовите известные методы расчета восстанавливаемых систем? 9. Как оценить время восстановления системы? 10. Какие законы распределения используются в надежности.
Литература: 1,2,3,6, 11.
Лекция 4 Тема: Методика оценки безотказности нерезервированных систем
План
1. Определение цели расчета надёжности ИС и их подсистем на этапе проектирования. 2. Методика и алгоритм оценки параметров безотказности для нерезервированных систем с последовательным соединением элементов. 3. Расчетные формулы оценки характеристик безотказности нерезервированных объектов. 4. Значение интенсивностей отказов для компонент ИС.
Ключевые слова Надёжность, методика, алгоритм, оценка параметров, характеристики надёжности, безотказность, последовательное соединение, нерезервированная система, интенсивность отказов, компоненты ИС, внезапный отказ.
Целью расчета надежности КС и их подсистем на этапе проектирования является [1, 2, 3, 6]: · сравнение вариантов при выборе технического решения; · получение приближенных оценок показателей надежности разрабатываемой ИС или подсистем (ЭВМ или блоков ЭВМ). Расчеты для оценки уровней надежности объектов выполняются приближенным методами, т.к. исходные данные о надежности весьма приближенные. В то же время сравнительные расчеты надежности целесообразно выполнить по точным методам, так как приближенные оценки не могут улавливать разницу в надежности тех или других технических решений. Методика оценки безотказности устройств ИС включает в себя следующие моменты: · определение типа элемента и его характеристик; · выбор метода расчета с последующим подбором определенных номограмм, таблиц, графиков или поправочных коэффициентов (вибрации, ударные нагрузки, температура, высота и т.д.); · определение электрических нагрузок и влияния внешней среды на каждой элемент; · определение по таблице или графику интенсивности отказа каждого элемента; · суммирование всех интенсивностей отказов для определения интенсивности отказов изделия. Расчет и оценка надежности устройств ИС и машин проводится в следующем порядке. 1. Формируется понятие отказа для рассматриваемого устройства и его отдельных составных частей. Прежде чем поступить к расчету надежности, необходимо четко сформулировать, что следует понимать под отказом устройства, а затем уже выбирать число элементов, которое должно быть учтено при расчете вероятности исправной работы или при расчете других количественных характеристик надежности (учитывать только те элементы, выход из строя которых приводит к отказу системы). 2. На основании анализа структуры устройства определяется основные и вспомогательные блоки устройства. 3. Составляется схема расчета надежности. Схему расчета необходимо составить таким образом, чтобы элементами расчета были конструктивно оформленные блоки. В устройствах в которых отсутствует элементная избыточность (т.е. нерезервированные системы), структурная схема расчета имеет вид последовательного соединения (рис. 1).
Рис. 1. Структурная схема расчета надежности
Пусть ИС состоит из n – элементов. Все элементы системы имеют свое функциональное назначение, следовательно здесь отказ любого элемента влечет за собой отказ системы. Схема расчета надежности будет представлять собой основное соединение. 4. Выбирается метод расчета надежности и производится оценка безотказности устройства по внезапным отказам. В соответствии с видом расчета выбираются расчетные формулы и для определения интенсивности отказов изделия по таблицам определяются величины интенсивности отказов элементов. Расчет надежности конструктивных единиц нерезервированных систем производится суммированием интенсивностей отказов.
а среднее время безотказной работы
Если система содержит Ni – элементов i -типа, а n 1 означает количество разновидностей элементов системы, то
где n 1 – число типов элементов, Ni – число элементов i -типа. Для определения интенсивности отказов типового элемента замены (ТЭЗ-ов) суммируются интенсивности отказов входящих в него ИС, паек, разъемов. Для определения надежности стойки суммируются интенсивности отказов входящих в нее панелей и других компонентов. Интенсивность отказов компьютера определяется суммированием интенсивностей отказов входящих в её состав подсистем, стоек и других составляющих конструкций. Если оценивается надежность не только аппаратуры, но всей ИС с учетом надежности программного обеспечения (ПО), необходимо к интенсивности отказов аппаратуры прибавлять также и интенсивность отказов ПО. Вероятность безотказной работы группы элементов при условии, что отказы элементов независимы, равна произведению вероятностей безотказной работы её элементов.
где Рi (t) – вероятность безотказной работы i -го элемента; n – число элементов, имеющих основное соединение. Для экспоненциального закона надежности ВБР определяется по формуле
Определение интенсивности отказов элементов осуществляется путем обработки статистических данных по результатам испытаний и эксплуатации. Приведем некоторые данные об интенсивностях отказов компонентов ИС (табл. 1). Приведенные цифры необходимо умножить на 10-6, чтобы получить значения интенсивностей отказов на час.
Таблица 1
5. Рассчитываются количественные характеристики надежности. Данные расчеты заносятся в итоговые таблицы или приводятся в виде графиков. Расчеты оформляются в виде технического отчета. Отчет должен содержать: а) структурную схему надежности системы с кратким объяснительным текстом; б) формулировку понятия отказа системы; в) расчетные формулы для количественных характеристик надежности; г) расчет количественных характеристик надежности; д) оценку точности расчета; е) выводы и рекомендации.
Контрольные вопросы и задания
1. В чем суть методики оценки безотказности нерезервированных систем? 2. Определите параметр надежности, который при экспоненциальном распределении остается постоянной величиной. 3. Составьте структурную схему надежности компьютера, состоящего из пяти устройств. 4. Перечислите основные моменты методики оценки надежности ИС. 5. Как определить интенсивность отказов ТЭЗ устройств ИС? 6. Что происходит в устройстве, структурная схема надежности которого имеет основное соединение, если один из элементов отказал? 7. Какова интенсивность отказов современного процессора?
Литература: 1,2,3,6, 8.
Лекция 5 Тема: Надёжность невосстанавливаемых и нерезервированных информационных систем
План
1. Расчетные формулы характеристик надёжности при основном соединение элементов ИС. 2. Прикидочный и ориентировочный методы расчета количественных характеристик устройств ИС. 3. Окончательный метод расчета надёжности ИС. Основные допущения и учёт режимов работы при окончательной расчете. 4. Применение перечисленных видов расчета на различных этапах проектирование ИС.
Ключевые слова Характеристика надёжности, основное соединение, прикидочный расчет, ориентированный расчет, окончательный расчет, количественные параметры, режим работы, нерезервированная система, этап проектирования, внешние воздействия.
Рассмотрим расчет характеристик надежности невосстанавливаемых изделий при основном соединении элементов. Если отказ технического устройства наступает при отказе одного из его элементов такое устройство имеет основное соединение элементов. При расчете надежности таких устройств предполагают, что отказ элемента является событием случайным и независимым. Тогда вероятность безотказной работы равна произведению вероятностей безотказной работы её элементов в течение времени t. Так как ВБР элементов в течение времени t можно выразить через интенсивность отказов, то расчетные формулы для ВБР устройства при основном соединении элементов можно записать следующим образом:
где N – число элементов. Выражения (2) наиболее общие. Они позволяют определить ВБР изделий до первого отказа при любом законе изменения интенсивности отказов во времени. На практике часто интенсивность отказов изделий является величиной постоянной. При этом время возникновения отказов обычно подчинено экспоненциальному закону распределения, т.е. для нормального периода работы аппаратуры справедливо условие λ =const. В этом случае выражения для количественных характеристик примут вид:
Если все элементы данного типа равнонадежны, интенсивность отказов системы будет
где Ni – число элементов i -го типа; r – число типов элементов. На практике очень часто приходится вычислять вероятность безотказной работы высоконадежных систем. При этом произведение λс∙t<< 1 значительно меньше единицы, а ВБР близка к единице. В этом случае, разложив Тогда основные количественные характеристики надежности можно с достаточной для практики точностью вычислить по следующим приближенным формулам:
Вычисление количественных характеристик надежности по приближенным формулам не дает больших ошибок для систем, ВБР которых превышает 0,9, т.е. для λ∙ t≤ 0,1. При расчете надежности систем часто приходится перемножать ВБР отдельных элементов расчета, возводить их в степень и извлекать корни. При вычислениях Р (t), близких к единице, эти вычисления можно с достаточной для практики точностью выполнять по следующим приближенным формулам:
где qi (t) – вероятность отказа i -го блока. В зависимости от полноты учета факторов, влияющих на работу изделия, различают прикидочный, ориентировочный и окончательный расчет надежности. Прикидочный расчет надежности. Прикидочный расчет основывается на следующих допущениях: · все элементы изделия равнонадежны; · опасности отказов всех элементов изделия не зависят от времени, т.е. λi=const; · отказ любого элемента приводит к отказу всего изделия. Прикидочный расчет надежности применяется в следующих случаях: 1) при проверке требований по надежности, выдвинутых заказчиком в техническом задании (ТЗ) на проектирование изделия; 2) при расчете нормативных данных по надежности отдельных блоков, устройств и приборов системы (расчет норм надежности отдельных частей системы); 3) для определения минимально допустимого уровня надежности элементов проектируемого изделия; 4) при сравнительной оценке надежности отдельных вариантов изделия на этапах эскизного проектирования. Прикидочный расчет надежности позволяет судить о принципиальной возможности обеспечения требуемой надежности изделия. Характеристики надежности рассчитываются по вышеприведенным формулам, при этом λс=N∙λэкв ., где λэкв. – эквивалентное значение интенсивности отказов элементов, входящих в изделие. Ориентировочный расчет надежности. Ориентировочный расчет надежности учитывает влияние на надежность только количества и типов примененных элементов и основывается на следующих допущениях: · все элементы данного типа равнонадежны, т.е. величины интенсивности отказов (λi) для этих элементов одинаковы; · все элементы работают в номинальном (нормальном) режиме, предусмотренном техническими условиями; · интенсивности отказов всех элементов не зависят от времени, т.е. в течение срока службы у элементов, входящих в изделие, отсутствует старение и износ, следовательно, λi (t) =const; · отказы элементов изделия являются событиями случайными и независимыми; · все элементы изделия работают одновременно. Для определения надежности изделия необходимо знать: 1) вид соединения элементов расчета надежности; 2) типы элементов, входящих в изделие, и число элементов каждого типа; 3) величины интенсивности отказов элементов λi, входящие в изделие. Выбор λi для каждого типа элементов производится по соответствующим таблицам. Таким образом, при ориентировочном расчете надежности достаточно знать структуру системы, номенклатуру примененных элементов и их количество. Ориентировочный метод расчета надежности используется на этапе эскизного проектирования после разработки принципиальных электрических схем изделий. Этот расчет позволяет определить рациональный состав элементов изделий и наметить пути повышения надежности изделия на стадии эскизного проектирования и проводится по формулам приведенным выше. Расчет надежности с учетом режимов работы элементов (окончательный). Окончательный расчет надежности изделия выполняется тогда, когда известны реальные режимы работы элементов после испытания в лабораторных условиях макетов и основных узлов изделия. Элементы изделия находятся обычно в различных режимах работы, сильно отличающихся от номинальной величины. Это влияет на надежность как изделия в целом, так и отдельных его составляющих частей. Выполнение окончательного расчета надежности возможно только при наличии данных о коэффициентах нагрузки отдельных элементов и при наличии графиков зависимости интенсивности отказов элементов от их электрической нагрузки, температуры окружающей среды и других факторов, т.е. для окончательного расчета необходимо знать зависимости λс = ƒ (Кн, Т 0, …)
Эти зависимости приводятся в виде графиков либо их можно рассчитывать с помощью так называемых поправочных коэффициентов интенсивности отказов Для определения надежности изделия необходимо знать: 1) число элементов с разбивкой их по типам и режимам работы; 2) зависимости интенсивности отказов элементов λi от электрического режима работы и заданных внешних условий; 3) структуру системы. В общем случае λi зависит от следующих воздействующих факторов: электрического режима работы данного элемента; окружающей температуры; вибрационных воздействий; механических ударов; линейных ускорений; влажности; воздействия биологических факторов (грибок, плесень, насекомые); давления; облучения и ряда других возможных факторов. При разработке и изготовлении элементов обычно предусматриваются определенные «нормальные» условия работы: температура +25±100С, номинальный электрический режим, относительная влажность 60±20%, отсутствие механических перегрузок и т.д. Интенсивность отказов элементов в номинальном режиме эксплуатации называется номинальной интенсивностью отказов λ 0 i. Интенсивность отказов элементов при эксплуатации в реальных условиях λi равна номинальной интенсивности отказов λ 0 i, умноженной на поправочные коэффициенты αi и ki. Поправочный коэффициент интенсивности отказов αi = ƒ (t 0, Кн) учитывает влияние окружающей температуры и электрической нагрузки, поправочный коэффициент интенсивности отказов ki = ƒ (j, φ) – тип воздействия, главным образом механические перегрузки и относительную влажность окружающего воздуха. Графики αi = ƒ (t 0, Кн) и ki = ƒ (j, φ) приведены в справочниках по расчету надежности (Ушаков И.А., Половко А.М.). Окончательный расчет надежности применяется на этапе технического проектирования изделия. Поправочные коэффициенты в зависимости от воздействий механических факторов, влажности, температуры и высоты приведены в табл. 1.
Таблица 1
При расчете изделие расчленяется на отдельные конструктивно самостоятельные части. Расчет производится последовательно от простого сложному.
Контрольные вопросы и задания
1. Напишите выражение по которой рассчитывается вероятность безотказной работы при последовательном соединение элементов ИС. 2. Какие приближенные формулы используются при расчете наработки на отказ и частоты отказов? 3. На каких допущениях основывается прикидочный расчет надежности? 4. В каких случаях используется ориентировочный расчет? 5. При каком методе расчета надежности учитываются режимы работы элементов ИС? 6. Что такое коэффициент нагрузки? 7. На каком этапе проектирования устройств ИС используется окончательный расчет надежности? 8. Приведите графическую зависимость l(t) от времени и объясните какой участок имеет l(t)=const.
Литература: 1,2,3,5,10.
Лекция 6 Тема: Структурное резервирование и его виды
План
1. Классификация структурного резервирования, основные определения. 2. Основные схемы расчета надёжности по способу включения резервных элементов: постоянное, раздельное, замещением, скользящее. 3. Виды резервных элементов и режимы работы при нагруженном, облегченном и ненагруженном резервах. 4. Расчетно-логическая схема структурного резервирования сложной системы. 5. Организация резерва на уровне элементов, устройств и систем ИС.
Ключевые слова Резервирование, избыточность, схема расчета, цифровое устройство, постоянное резервирование, раздельное резервирование, резервирование замещением, нагруженный резерв, ненагруженый резерв, режимы работы, скользящий резерв, переключающая схема, надёжность, безотказность.
Резервированием называют метод повышения надежности объекта путем введения избыточности. Задача введения избыточности – обеспечить нормальное функционирование системы после возникновения отказов в ее элементах. Резервирование может быть структурным, информационным, временным, программным. Информационное резервирование предусматривает использование избыточной информации. Временное резервирование – использование избыточного времени. Программное резервирование – избыточных программ. Структурное резервирование заключается в том, что в минимально необходимый вариант системы, элементы которой называются основными, вводятся дополнительные элементы и устройства, либо вместо одной системы предусматривается использование нескольких идентичных систем. При этом избыточные резервные структурные элементы берут на себя выполнение рабочих функций при отказе основных элементов [1, 2, 3, 5]. Перечисленные виды резервирования могут быть применены либо к системе в целом, либо к отдельным ее элементам или их группам. На практике большое распространение получило структурное резервирование (рис. 1).
Рис. 1. Способы резервирования КС
По схеме включения резервных элементов различают постоянное, раздельное резервирование, резервирование с замещением и скользящее резервирование. Постоянное резервирование – это такое резервирование, при котором резервные элементы участвуют в функционировании объекта наравне с основными (рис. 2). Для постоянного резервирования в случае отказа основного элемента не требуется специальных устройств, вводящих в действие резервный элемент, так как он вводится в действие одновременно с основными. Основным параметром резервирования является его кратность (степень избыточности). Под кратностью резервирования m понимается отношение числа резервных объектов к числу резервируемых (основных). Раздельным резервированием называется метод повышения надежности, при котором резервируются отдельные части объекта (рис. 2.3).
Рис. 2. Общее резервирование и постоянное включение резерва с постоянно включенным резервом.
Рис. 3. Раздельное резервирование с постоянно включенным резервом
Резервирование замещением – это резервирование, при котором функции основного элемента передаются резервному только после отказа основного (рис. 4 а, б). При использовании резервирования замещением необходимы контролирующие и переключающие устройства для обнаружения факта отказа основного элемента и переключения его с основного на резервный.
Рис. 4. а) Общее резервирование с включением резерва замещением. б) Раздельное резервирование с включением резерва замещением.
Скользящее резервирование – это резервирование замещением, при котором группа основных элементов объекта резервируется одним или несколькими резервными, каждый из которых может заменить любой отказавший элемент в данной группе. Скользящее резервирование всегда является активным, всегда имеется переключающее устройство, определяющее наличие отказа и включающее резервный элемент (рис. 5).
Рис. 5. Схема скользящего резервирования
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 1591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.045 с.) |

 , (7)
, (7)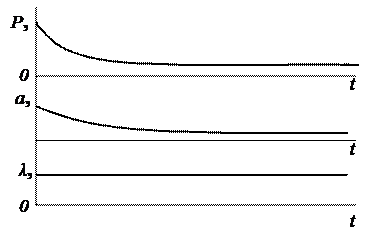
 (10)
(10) (11)
(11) , (12)
, (12) .
. .
. .
. .
.
 ,
, .
. ,
, ,
, .
. , (1)
, (1) (2)
(2) ,
,  ,
, ,
,  .
. ,
, в ряд и ограничившись первыми двумя членами, с высокой степенью точности можно вычислить Р (t).
в ряд и ограничившись первыми двумя членами, с высокой степенью точности можно вычислить Р (t). , (3)
, (3) ,
,  . (4)
. (4) , (5)
, (5) , (6)
, (6) , (7)
, (7) , позволяющих учесть влияние различных факторов на надежность изделия.
, позволяющих учесть влияние различных факторов на надежность изделия.














