
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи оптимального резервирования компьютерных системСодержание книги
Поиск на нашем сайте
Как уже отмечалось, резервирование является одним из простых и достаточно эффективных методов повышения надежности. Однако при резервировании возникает задача не только обеспечить заданные показатели надежности, но добиться этого как можно более экономично, с наименьшими суммарными затратами на резервные элементы для системы в целом, либо при заданных ресурсных ограничениях достичь максимально возможной надежности. Задача оптимального резервирования чаще возникает в отказоустойчивых системах позволяющих пользователю или функциональной программе продолжать работу и тогда, когда в аппаратных или программных средствах системы возникают отказы. При проектировании таких систем следует стремиться не только к достижению необходимой их надежности, но и к достижению этой надежности при минимальных средствах, т.е. к нахождению оптимального решения. В отказоустойчивых компьютерных системах и машинах существует ряд параметров, от которых зависит надежность системы. Сюда относится количество резервных элементов, устройств или подсистем; параметры систем контроля и диагностики; характеристики системы программного обеспечения; величины, характеризующие архитектуру, конфигурацию работы системы и другие:
Надежность представляется в виде функциональной зависимости от перечисленных параметров. В качестве подобных ограничивающих ресурсов можно рассмотреть стоимость, массу, габаритные размеры, потребляемую мощность и т.п. Выбор вида ограничивающего ресурса определяется конкретным типом системы и ее назначением. Часто выделяют одну наиболее важную характеристику – стоимость. Обычно в задачах оптимального резервирования предполагается, что стоимость резерва для системы в целом:
где и кроме того, сама стоимость резерва i -й резервной группы определяется как:
где При наличии одного ограничивающего фактора (стоимости) возможны постановки двух следующих задач оптимального резервирования [1, 3, 13]. 1. Прямая задача. Раздельным резервированием системы, состоящей из m -резервных групп, добиться того, чтобы показатель надежности был не менее заданного Rзад при минимально возможной стоимости резерва в целом, т.е.:
2. Обратная задача. Раздельным резервированием системы, состоящей из m -резервных групп, добиться того, чтобы при максимально возможном показателе надежности системы R стоимость всего резерва не превысила заданного значения Сзад, т.е.:
если в качестве показателя надежности выбрать ВБР Рс, то:
где Сi – стоимость одного блока в i -й подсистеме компьютера или КС; mi – число резервных блоков в i -й подсистеме компьютера или КС; Cзад – заданное значение стоимости резервных блоков машины или КС; Pc – вероятность безотказной работы КС за время Т. Суть оптимизационной задачи, заключающейся в повышении надежности системы путем резервирования при ограничениях на суммарную стоимость, можно пояснить на двух простых частных случаях. Допустим, что все элементы системы равнонадежны и в каждой резервной группе имеется ровно по одному основному элементу. В этом случае приоритет по резервированию сначала получают те группы, элементы которых характеризуются наименьшей стоимостью. Если же элементы имеют равную стоимость, то сначала следует резервировать наименее надежные резервные группы. В более сложных случаях, когда резервные группы содержат различное число элементов, а сами элементы в различных группах различаются и по показателям надежности, и по стоимости, для определения оптимального состава резервных элементов в системе требуется использовать специальные алгоритмы решения оптимизационных задач [13, 15, 18]. Экспериментальные задачи (задачи нахождения экстремума функции min или max) с ограничениями могут быть решены аналитически (с использованием метода неопределенных множителей Лагранжа) и с помощью численных методов: метода перебора и градиентного метода. При решении оптимизационных задач могут быть ограничения на массу, стоимость, габариты и другие характеристики системы. Рассмотрим, как может быть сформулирована оптимизационная задача резервирования с учетом одного параметра – стоимости. Задача оптимизации компьютерных систем по показателю надежности заключается в таком резервировании каждой из подсистем, которое доставляет максимальную безотказность всей системы при заданных ограничениях на ее стоимость – С (mi) ≤ Сзад, или можно найти вектор mi, представляющий собой решение задачи:
где mi – число резервных блоков в i -й подсистеме ВС; Сi – стоимость одного блока в i -й подсистеме; Cзад – заданное значение стоимости резервных блоков ВС; Pc – вероятность безотказной работы КС за время Т. Может быть решена и обратная задача. Оптимальное распределение резервов в КС на уровне процессоров, устройств или подсистем рассмотрим с использованием аналитического приближенного метода неопределенных множителей Лагранжа. Пусть имеем систему с нагруженным резервом, подключенным по схеме поэлементного резервирования. Каждая из n -подсистем (процессоры, ОЗУ, ПУ и др.) имеют mi -1 резервов. Вероятность безотказной работы (ВБР) i -й подсистемы (
Чтобы упростить формулу, допустим, что
где m = (m 1, m 2 ,…, mn). Масса, габариты или стоимость системы выражается в виде линейной зависимости:
где ci – стоимость i -й подсистемы. Необходимо определить min Q (m) при условии, что C (m) ≤ Сзад, где Сзад – заданное значение стоимости системы. Искомыми являются значения mi, минимизирующие вероятность отказа Q. Поскольку Q (m) и C (m) монотонные зависимости, то условие типа неравенства может быть заменено условием типа равенства, а задача решена методом неопределенных множителей Лагранжа. Функция Лагранжа F (m) имеет следующий вид:
где ξ – неопределенный множитель Лагранжа. Совместное решение необходимых условий экстремума (4):
и условие типа равенства:
позволяют определить n оптимальных значений mi и соответствующее им значение неопределенного множителя ξ. Подставляя Q (m), C (m), из (2), (3) в 4, а F (m) из (4) в (5) получим следующую систему уравнений:
где αi = ci / ln(qi). Для определения ξ поставим mi, из в (6), тогда:
В последнем выражении изменены знаки сомножителей ξ и αi, т.е. вместо ξ и αi написано (-ξ) и (- αi) для того, чтобы можно было логарифмировать, так как αi ≤ 0. Следовательно, решение существует только в случае, когда ξ – отрицательная величина. Выражая ln(- ξ) и подставляя, получим окончательное выражение для оптимальных значений mi:
При второй постановке задачи решение осуществляется согласно (min(max) φ (x),
где Н – ограничение, налагаемое на показатель надежностиП(х)) на основании следующей функции Лагранжа:
где η – неопределенный множитель Лагранжа; Qзад – заданное значение вероятности отказа. Решая совместно уравнения
Приведенные выражения являются приближенными из-за необходимости округления результата. Ошибка получается особенно большая при малых mi. Кроме того, аналитический метод позволяет получить решение в явном виде только при простейших моделях надежности.
|
||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 .
.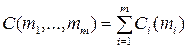
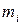 – число резервных блоков в i -ой подсистеме КС;
– число резервных блоков в i -ой подсистеме КС;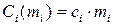
 – стоимость одного блока в i -ой подсистеме КС.
– стоимость одного блока в i -ой подсистеме КС. .
.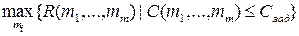 ,
,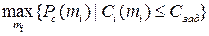 ,
,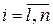 ) обозначается через Рi. Тогда ВБР системы Рс выражается как:
) обозначается через Рi. Тогда ВБР системы Рс выражается как: . (1)
. (1)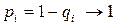 , где qi – вероятность отказа i -й подсистемы. Тогда вероятность отказа системы Q:
, где qi – вероятность отказа i -й подсистемы. Тогда вероятность отказа системы Q: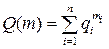 , (2)
, (2)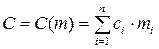 , (3)
, (3)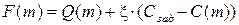 , (4)
, (4) , (5)
, (5)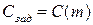 , (6)
, (6) , откуда,
, откуда, 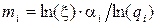 , (7)
, (7)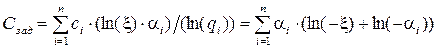 . (8)
. (8)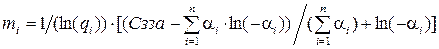 , (9)
, (9)
 ,
,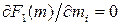 при
при  и
и 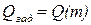 , получим вқражение для оптимальных кратностей резервирования:
, получим вқражение для оптимальных кратностей резервирования: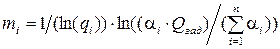 . (10)
. (10)


