
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальное распределение резервов численными методамиСодержание книги
Поиск на нашем сайте
Задача оптимального резервирования может быть решена не только аналитически (методом неопределенных множителей Лагранжа), но и численными методами. Численные методы определения оптимального резерва позволяют найти более точное решение, и особенно эффективны при малом числе резервных подсистем. К численному методу относится метод перебора, когда сравнивают между собой все возможные варианты структуры. Затем выбирают из них тот, который лучше всего отвечает установленным требованиям по надежности. Однако число вариантов получается практически весьма большое, поэтому метод перебора может быть использован только в простейших случаях. Обозначим количество конкурирующих вариантов Nb. Для структуры сложной КС типа Nb определяется произведением:
где
Например, Рассмотрим возможность сокращения числа вариантов при переборе. Введем понятие доминирующий последовательности и рассмотрим график вариантов технический решений в координатах: стоимость С – вероятность отказа Q (рис.1).
Рис. 1. Графическая иллюстрация доминирующей последовательности
Каждый вариант этом графике представляется точкой. Из всех вариантов заданной стоимости С интерес представляют только варианты, обладающие минимальной вероятностью отказа Q. Из вариантов при заданной (ими меньшей) вероятности отказа Q интересны только варианты, отличающиеся минимальной стоимостью С. Отсюда следуют, что из всего множества вариантов интерес представляют только те, которые находятся снизу и слева. Подмножество этих вариантов, перспективных с точки зрения поиска оптимального варианта, называется доминирующей последовательностью. На рис. 1 доминирующая последовательность обведена. Мощность (количество элементов) доминирующей последовательности обычно намного меньше мощности множества вариантов. Поэтому легко выбирать оптимальное решение из вариантов, входящих в доминирующую последовательность. Численные методы позволяют построить доминирующую последовательность поэлементно, – до достижения заданной надежности при минимальной стоимости или до достижения минимальной стоимости при заданной надежности. При структурной оптимизации важно найти эффективный способ ограничения количества рассматриваемых вариантов.
Эффективным методом является градиентный метод заключается в пошаговом поиске максимума критерия типа ∆lg(Q) / (∆ С), т.е. отношения приращения логарифма вероятности отказа системы к приращению стоимости [1, 12, 42, 49]. Градиентный метод позволяет определить часть элементов доминирующей последовательности, т.е. некоторые элементы могут отказаться пропущенными. Поэтому получаемые этим методом результаты следует рассматривать как приближенные или проводить дополнительный поиск. Пример оптимального распределения резервов. Пусть имеется система, состоящая из четырех подсистем, т.е. n = 4. подсистемы характеризуются стоимостями Ci и вероятностями отказа за заданное время qi:
Требуется построить систему, обладающую вероятностью безотказной работы Р ≥ 0, 99 при минимальной стоимости С. Первоначальное состояние системы, когда нет резервов, описываются вектором состояний
Контрольные вопросы и задания 1. Что такое резервирование? 2. Какие виды структурного резервирования широко распространены на практике? 3. Для каких компьютерных систем решаются задачи оптимального резервирования? 4. Какие аналитические и численные методы используются при оптимальном резервировании КС? 5. Определите суть метода Лагранжа для оптимизации надежности. 6. Дайте формулу для расчета нахождения резервного элемента в КС ответственного назначения. 7. Что такое градиентный метод? 8. Укажите метод при оптимизации резервов в КС, где используется понятие «доминирующая последовательность».
Литература: 1, 2, 5, 6, 9, 10.
З А К Л Ю Ч Е Н И Е
Развитие информационных систем в настоящее время осуществляется по следующим основным направлениям: создание высоконадежных аппаратных и программных средств компьютерной техники; суперкомпьютеров большой производительности; систем с высокой степенью интеллекта; обширных компьютерных сетей с огромными банками данных; персональных компьютеров массового применения; микропроцессорных средств управления для различных машин и аппаратов.
Успешная реализация возможностей всех этих направлений предполагает весьма высокую достоверность получаемых с помощью компьютера результатов при ограниченном числе ремонтного персонала. Выполнение этого условия возможно только при систематическом планировании, учете и реализации факторов, обеспечивающих надежность и отказоустойчивость получаемых результатов при высокой степени автоматизации процесса эксплуатации вычислительных средств. Проблема надежности вычислений и достоверности их результатов в ИС существовала всегда. Однако при небольших объемах и скоростях вычислений и при решении не очень ответственных задач отдельные ошибочные результаты легко обнаруживались и не причиняли особого вреда. Неисправность простых и немногочисленных компьютеров того времени тоже можно было легко устранить. В настоящее время в связи с непомерно возросшими объемами и скоростями вычислений и с высокими требованиями к достоверности результатов обработки данных поддерживание работоспособности ИС может быть достигнуто путем его полной автоматизации. Учитывая стремительные темпы дальнейшего роста быстродействия и производительности компьютерных средств, можно с уверенностью сказать, что всякие другие пути поддержания работоспособности ИС, кроме его полной автоматизации, наталкивается на непреодолимые трудности, связанные с нехваткой обслуживающего персонала. Процесс развития ИС не может быть преодолен просто наращиванием компьютерных мощностей. В области обеспечение работоспособности средств компьютерной техники (СКТ) зарождаются новые в принципе технические решения. С одной стороны, эти решения базируются на новой элементной базе, а с другой – на новых логических, структурных и алгоритмических принципах построения СКТ. Существующие технические решения, основанные на трех-или четырех кратном увеличении аппаратуры и программных средств для достижения увеличения устойчивости ИС к отказам и ошибкам вряд ли соответствуют по уровню отработанности и по изяществу замысла другим техническим решениям, принятым в современной компьютерной технике. В данной области существует широкое поле поиска развития общей теории отказоустойчивых КС, так и в плане изобретательской деятельности для решения частных задач. Очевидно, решение проблемы отказоустойчивости ИС тесно связано с проблемой распараллеливания вычислений, построения компьютерных сетей, а возможно, с новыми результатами в области применения теории групп и других отраслей современной математики к развитию арифметических и логических основ построения СКТ. Литература 1. Иыуду К.А Надежность, контроль и диагностика вычислительных машин и систем. М: Высшая школа, 1989-216с 2. Расулова С.С Надежность вычислительных машин и систем. Учебное пособие, ТашГТУ, 1995-60с 3. Расулова С.С Надежность ЭВС. Конспект лекций. ТашГТУ, 2001-90с 4. Расулова С.С. Рашидов А.А. Программа, методические указания, ТашГТУ-2003. 5. Расулова С.С., Рашидов А.А. Построение отказоустойчивых микропроцессорных систем. Ташкент –Mehnat -2004.
6. Расулова С.С. Обеспечение надежности и отказоустойчивости компьютерных систем. Проблемная лекция. ТашГТУ, 2004-27с 7. Дружинин Г.Н. Надежность автоматизированных произвоственных систем. М: Энергаатомиздат 8. Иыуду К.А. Задачи и упражнения по основам эксплуатации электронных приборов. М: МАИ, 1996-120с 9. Самопалов К.Г. и др. Цифровые ЭВМ. Практикум. Киев. Высшая школа. 1990-125с. 10. Бройдо В.Л. Вычислительные системы, сети и телекоммуникации. 2 изд. Учебник. СПб.: «Питер», 2005. глава 20, -703 с. 11. Степанов А.Н. Архитектура вычислительных систем и компьютерных сетей. Учебное пособие. – СПб.: Питер, 2007. -509 с.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.176.19 (0.01 с.) |

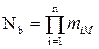 ,
,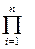 – общее число подсистем;
– общее число подсистем;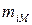 – максимально возможное число параллельных подсистем i -го типа.
– максимально возможное число параллельных подсистем i -го типа. и
и 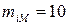 , при
, при  , тогда Nb = 1010, это практически исключает возможность перебора.
, тогда Nb = 1010, это практически исключает возможность перебора.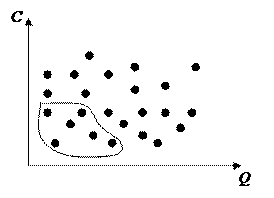
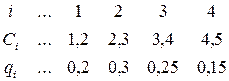
 . Сравнение вариантов (2111), (1211), (1121) и (1112) происходит по критерию ∆lg(Q) / ∆ С, обеспечивающего максимум критерия. Используя приведенные выше формулы находим приближенное решение задачи. Величина оптимального распределения резерва m = (5543).
. Сравнение вариантов (2111), (1211), (1121) и (1112) происходит по критерию ∆lg(Q) / ∆ С, обеспечивающего максимум критерия. Используя приведенные выше формулы находим приближенное решение задачи. Величина оптимального распределения резерва m = (5543).


