Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод переходных интенсивностейСодержание книги
Поиск на нашем сайте
Экспоненциальное распределение с удовлетворительной точностью описывает функционирование систем и их элементов на участке нормальной эксплуатации. Экспоненциальное распределение описывает процессы в системах без предыстории, поскольку изменение вероятности их нахождения в том или ином состоянии за интервал зависит только от длительности временного интервала. Так снижение вероятности работоспособного состояния d Po (t) = -λ* e-λt dt= λ*Po (t) dt, а вероятности состояния восстановления dP1 (t) = -μ* e-μt * dt= μ *P1 (t) dt. Если система может находиться только в двух состояниях – восстановление и работы, то снижение вероятности одного состояния приводит к соответствующему увеличению вероятности другого состояния, поскольку для любого момента времени dP1 (t)+ dPo (t)=1. Таким образом, вероятности нахождения систем в момент t+dt в каждом из состояний связаны с соответствующими вероятностями: P0(t+Dt)=P0(t)-lP0 (t)d t +mP1 (t) d t P1(t+Dt)=P1(t)- m P1 (t)d t + l P0 (t) d t (8.8) Сопоставляя (8.5) и (8.8) определим, что (1- λ* dt) =p11; λ* dt=p12 ;(1- μ * dt) =p22; μ * dt=p21; Теперь можно составить матрицу переходов (8.7). Так как [Pi (t+dt)- Pi (t)] /dt= dPi (t) /dt, то вероятность нахождения системы с непрерывным временем в каждом из состояний определяется следующей системой дифференциальных уравнений первого порядка, называемой системой Колмогорова-Чепмена: P0(t)/dt=- lP0 (t)+ mP1 (t); P1(t)/dt=lP0 (t)- mP1 (t); (8.9)
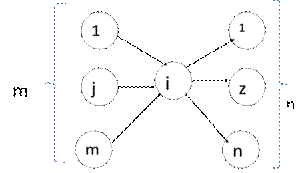
В общем случае число дифференциальных уравнений определяется числом возможных состояний системы, которое (как и для систем с дискретным временем) должно быть ограничено. При записи дифференциальных уравнений предварительно составляется перечень возможных состояний системы и соответствующий ему ориентированный граф состояний, подобный представленному на рисунке 8.1. Каждая из вершин соответствует одному из состояний системы, а ориентация ребер определяется направлением перехода. Так, граф состояний рассмотренный выше системы с двумя состояниями обычно изображается в виде, представленном на рисунке 8.3,а.
а) б) Рисунок 8.3 Граф состояния восстанавливаемой системы Для произвольной вершины i (рисунок 8.3,б), в которую система может прийти из m вершин и из которой переходит в одну из n вершин: m n dPi (t) /dt =Σ Λji dPj (t) - Pi (t) Σ Λiz (8.10) j=1 z=1 Проверкой правильности составления системы дифференциальных уравнений является равенство нулю суммы правых частей уравнений. При анализе надежности восстанавливаемых систем с непрерывным временем возникают две группы задач. Первая связана с определением функций и коэффициентов готовности и простоя, параметра потока отказов, вторая – с расчетом вероятности безотказной работы и средней наработки до отказа. При решении задач первой группы состояния. В которых система восстанавливается после отказа, являются отражающими, то есть после завершения восстановления система возвращается в одно из работоспособных состояний. При решении второй группы задач состояния восстановления системы являются поглощающими и интенсивности выхода из этих состояний исключаются. Поскольку функция готовности КГ(t) определяет вероятность нахождения системы в работоспособном состоянии в момент времени t, то:
где j и z – работоспособные и неработоспособные состояния системы. Функция простоя:
Для определения коэффициента готовности kГ может быть применено несколько приемов. Один из них основан на непосредственном расчете предела -λ *Po + μ *P1 =0; Po + P1=1; откуда kГ = Po= μ/(μ + λ) Очевидно, что аналогом коэффициента готовности непрерывных систем для систем с дискретным временем является предельная вероятность нахождения системы в работоспособном состоянии, определяемая системой алгебраических уравнений (8.9). Поток отказов и ведущая функция восстанавливаемой системы:
Средняя наработка между отказами на интервале t:
При стационарном процессе восстановления, когда t→∞ Для рассматриваемой выше системы с двумя состояниями: ω(t) = λ *Po(t)= λ *Kг(t)
t→∞ ω = λ *Po= λ *Kг; τср = 1/ λ; (8.13) При решении второй группы задач в системе дифференциальных уравнений исключаются члены, содержащие в качестве сомножителей интенсивности выхода из поглощающего состояния. В этом случае вероятность безотказной работы Используем рассмотренный метод анализа для оценки показателей надежности более сложных восстанавливаемых систем, в частности включающих n последовательно соединенных нерезервированных элементов, каждый из которых характеризуется интенсивностями отказов li и mI восстановления. Рассмотрим простой вариант задачи, при котором после отказа любого из элементов система отключается. Структурная схема такой системы представлена на рисунке 5.1, а граф состояния на рисунке 8.4.
Рисунок 8.4 – Граф состояния системы n последовательно соединенных элементов Во всех состояниях, кроме нулевого, система отключена и производится восстановление соответствующего элемента. Надежность системы в любой момент времени характеризуется следующими дифференциальными уравнениями:
Функция готовности с преобразованием Лапласа:
Лекция 9
Цель лекции: Обучение основных практических методов оценки надежности по результатам испытаний.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.161.199 (0.008 с.) |




 при t→∞. Второй использует предельную теорему, согласно которой
при t→∞. Второй использует предельную теорему, согласно которой  , где р = переменная преобразования Лапласа;
, где р = переменная преобразования Лапласа;  - изображение по Лапласу функции
- изображение по Лапласу функции  Коэффициент готовности можно рассчитать по системе дифференциальных уравнений путем приравнивания нулю dPi (t)/ dt = 0 и решения системы алгебраических уравнений относительно всех работоспособных состояний системы. Так, для системы (8.9) алгебраические уравнения для расчета kГ имеют вид:
Коэффициент готовности можно рассчитать по системе дифференциальных уравнений путем приравнивания нулю dPi (t)/ dt = 0 и решения системы алгебраических уравнений относительно всех работоспособных состояний системы. Так, для системы (8.9) алгебраические уравнения для расчета kГ имеют вид:

 где Pj = lim Pj(t) - финальная вероятность j-го работоспособного состояния. Средняя наработка на отказ τ= kг/ ω.
где Pj = lim Pj(t) - финальная вероятность j-го работоспособного состояния. Средняя наработка на отказ τ= kг/ ω.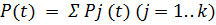 , где
, где 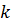 - все работоспособные состояния системы. Среднее время безотказной работы рассчитывается как τср(t) = ∫ P0 (t) dt.
- все работоспособные состояния системы. Среднее время безотказной работы рассчитывается как τср(t) = ∫ P0 (t) dt.