
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 1: Матрицы и системы линейных алгебраических уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Лекция 1. Пространство арифметических векторов. Линейная зависимость и линейная независимость арифметических векторов, необходимое и достаточное условие линейной зависимости. Минор матрицы. Базисный минор. Теорема о базисном миноре и её следствие для квадратной матрицы. ОЛ-1 гл.6 п.6.7; гл.8 п.8.4-8.5; ОЛ-4 гл.1 пар.3 п.1-2; ОЛ-5 гл.5 пар. 4. Лекция 2. Ранг матрицы. Теорема о ранге матрицы (без док-ва). Инвариантность ранга матрицы относительно элементарных преобразований (без док-ва). Методы вычисления ранга матрицы. Системы линейных алгебраических уравнений (СЛАУ). Координатная, матричная и векторная форма записи. Критерий Кронекера-Капелли совместности неоднородной системы линейных уравнений. ОЛ-1 гл.8 п.8.4 – 8.6; гл.9 п.9.1-9.3; ОЛ-4 гл.1 пар.3; гл.3 пар.1; ОЛ-5 гл.5 пар. 4-5. Лекции 3–4. Решение систем линейных алгебраических уравнений. Однородные системы линейных алгебраических уравнений. Свойства решений однородной системы. Теорема о числе линейно независимых решений однородной СЛАУ. Фундаментальная система решений однородной СЛАУ. Теорема о структуре общего решения неоднородной СЛАУ. Свойства решений неоднородной и соответствующей однородной системы. Построение нормальной фундаментальной системы решений системы линейных однородных уравнений и частного решения совместной неоднородной системы линейных уравнений. ОЛ-1 гл.9 п.9.5 – 9.7; ОЛ-4 гл.3 пар.2; ОЛ-5 гл.5 пар. 5. Модуль 2: Линейные и евклидовы пространства Лекция 5. Аксиоматика линейного пространства. Примеры линейных пространств. Следствия из аксиом. Линейные комбинации векторов, линейно зависимые и линейно независимые системы векторов, критерий линейной зависимости и независимости векторов. Свойства линейно зависимых и линейно независимых систем векторов. Размерность и базисы линейного пространства. Разложение вектора по базису, единственность разложения. Конечномерные линейные пространства. ОЛ-2 гл.1 п.1.1 – 1.7; ОЛ-4 гл.2 пар.1-2; ОЛ-5 гл.6 пар. 1. Лекция 6. Координаты вектора. Линейные операции над векторами в координатной форме. Переход к новому базису, матрица перехода. Преобразование координат вектора при переходе к другому базису. Подпространства линейных пространств, их свойства, размерность. Линейная оболочка системы векторов. Ранг системы векторов. ОЛ-2 гл.1 п.1.6, 1.8; гл.2 п.2.1-2.2, 2.4-2.6; ОЛ-4 гл.2 пар.2-4; ОЛ-5 гл.6 пар. 1-2. Лекция 7. Аксиоматика евклидова пространства, скалярное произведение. Примеры евклидовых пространств. Неравенство Коши-Буняковского. Нормированное пространство. Норма вектора и её свойства. Угол между векторами. Ортогональные векторы, линейная независимость ортогональной системы векторов. ОЛ-2 гл.3 п.3.1 –3.5; ОЛ-4 гл.4 пар.1-3; ОЛ-5 гл.7 пар.1. Лекция 8. Ортонормированный базис евклидова пространства, его построение из произвольного базиса с помощью процесса ортогонализации Грама-Шмидта. Скалярное произведение векторов в произвольном и ортонормированном базисах. Матрица Грама и её свойства. ОЛ-2 гл.3 п.3.6 – 3.8; ОЛ-4 гл.4 пар.2 п.1-4; ОЛ-5 гл.7 пар. 1,3. Лекция 9. Ортогональные матрицы и их свойства. Теорема о матрице перехода от ортонормированного базиса к ортонормированному базису. Изоморфизм линейных и евклидовых пространств. Теорема об изоморфизме конечномерных линейных пространств. Теорема об изоморфизме конечномерных евклидовых пространств. ОЛ-2 гл.7 п.7.1, 7.3; гл.4 п.4.2; ОЛ-5 гл.7 пар.1 п.6; гл.6 пар.3 п.3. Модуль 3: Линейные операторы Лекция 10. Понятие линейного оператора. Примеры. Матрица линейного оператора, ее преобразование при замене базиса. Подобные матрицы. Линейные операции над линейными операторами. Произведение линейных операторов. Связь между операциями с линейными операторами и операциями с их матрицами. Обратный оператор и его матрица. ОЛ-2 гл.4 п.4.1 – 4.5; ОЛ-4 гл.5 пар.1-2; ОЛ-5 гл.6 пар.3. Лекция 11. Собственные значения и собственные векторы линейного оператора, их нахождение. Характеристический многочлен, его инвариантность относительно выбора базиса. Линейная независимость собственных векторов, соответствующих различным собственным значениям. Матрица линейного оператора в базисе из собственных векторов. ОЛ-2 гл.5 п.5.1 – 5.5; ОЛ-4 гл.5 пар.3; ОЛ-5 гл.6 пар. 4. Лекция 12. Линейные операторы в евклидовых пространствах. Сопряженный оператор. Линейность сопряженного оператора. Матрица сопряженного оператора в ортонормированном базисе. Свойства сопряженного оператора. ОЛ-2 гл.6 п.6.1; ОЛ-4 гл.5 пар.5 п.1; ОЛ-5 гл.7 пар. 2. Лекция 13. Самосопряженный (симметрический оператор), симметричность его матрицы в ортонормированном базисе. Свойства собственных значений и собственных векторов самосопряженного линейного оператора. Существование ортонормированного базиса евклидова пространства из собственных векторов самосопряженного оператора. ОЛ-2 гл.6 п.6.2 – 6.3; ОЛ-4 гл.5 пар.5 п.2; ОЛ-5 гл.7 пар. 2. Лекция 14. Ортогональный оператор. Свойства ортогонального оператора. Теорема об ортогональности его матрицы в ортонормированном базисе. Ортогональные преобразования координат. Приведение матрицы самосопряженного оператора к диагональному виду с помощью ортогонального преобразования. ОЛ-2 гл.7 п.7.2 – 7.4; ОЛ-4 гл.5 пар.9; ОЛ-5 гл.7 пар.2. Модуль 4: Квадратичные формы Лекции 15–16. Квадратичная форма в евклидовом пространстве и связанный с ней симметричный оператор. Изменение матрицы квадратичной формы при замене переменных. Канонический вид квадратичной формы. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования. Канонический вид квадратичной формы в ортонормированном базисе из собственных векторов этого оператора. Метод Лагранжа приведения квадратичной формы к каноническому виду. Закон инерции квадратичных форм (без док-ва). Знакоопределенность квадратичных форм и их матриц. Критерий Сильвестра (без док-ва). ОЛ-2 гл.8 п.8.1 – 8.6; ОЛ-4 гл.7 пар.2-4, 6; ОЛ-5 гл.8 пар. 2-3. Лекция 17. Общие уравнения кривых и поверхностей второго порядка, их приведение к каноническому виду. Классификация кривых и поверхностей второго порядка. ОЛ-2 гл.9 п.9.1 – 9.6; ОЛ-4 гл.7 пар.6-7. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Модуль 1: Матрицы и системы линейных алгебраических уравнений Занятие 1. Нахождение ранга матрицы. Ауд.: ОЛ-7 гл.3: № 3.150; 3.154; 3.156; 3.159; 3.163; 3.166. Дома: ОЛ-7 гл.3: № 3.151; 3.153; 3.157; 3.165; 3.168. Занятие 2. Решение систем линейных однородных уравнений. Ауд.: ОЛ-7 гл.3: № 3.223; 3.224; 3.225; 3.228; 3.235; 3.230. Дома: ОЛ-7 гл.3: № 3.226; 3.227; 3.229; 3.231; 3.232; 3.234. Занятия 3–4. Решение систем линейных неоднородных уравнений. Ауд.: ОЛ-7 гл.3: № 3.206; 3.210; 3.208; 3.239; 3.218; 3.220. Дома: ОЛ-7 гл.3: № 3.207; 3.209; 3.211; 3.212; 3.236; 3.238; 3.219; 3.221. Занятие 5. Рубежный контроль по модулю 1. Модуль 2: Линейные и евклидовы пространства Занятие 6. Линейные пространства, размерность, базис. Матрица перехода от одного базиса к другому. Изменение координат вектора при переходе к новому базису. Ауд.: ОЛ-7 гл.4: № 4.1 – 4.9 (неч); 4.15; 4.17; 4.18; 4.23; 4.25; 4.30; 4.37. Дома: ОЛ-7 гл.4: № 4.2 – 4.10 (чет); 4.16; 4.20; 4.24; 4.28; 4.31; 4.38. Занятие 7. Ранг системы векторов. Линейная оболочка системы векторов. Подпространство линейного пространства. Ауд.: ОЛ-7 гл.4: № 4.19; 4.21; 4.45; 4.47; 4.52; 4.54. Дома: ОЛ-7 гл.4: № 4.46; 4.48; 4.51; 4.53. Занятие 8. Евклидово пространство. Процесс ортогонализации. Ауд.: ОЛ-7 гл.4: № 4.67; 4.71; 4.74. Дома: ОЛ-7 гл.4: № 4.69; 4.72; 4.76. Занятие 9. Рубежный контроль по модулю 2. Модуль 3: Линейные операторы Занятие 10. Линейные операторы и их матрицы. Ауд.: ОЛ-7 гл.4: № 4.86; 4.89; 4.90; 4.91; 4.94; 4.97. Дома: ОЛ-7 гл.4: № 4.85; 4.87; 4.92; 4.93; 4.95; 4.99. Занятие 11. Преобразование матрицы линейного оператора при переходе к новому базису. Собственные значения и собственные векторы линейного оператора. Ауд.: ОЛ-7 гл.4: № 4.106(а); 4.107; 4.135; 4.137; 4.139; 4.140. Дома: ОЛ-7 гл.4: № 4.106 (б); 4.134; 4.136; 4.138; 4.141. Занятие 12. Матрица сопряженного оператора. Приведение матрицы линейного оператора к диагональному виду. Ауд.: ОЛ-7 гл.4: № 4.151; 4.176; 4.175; 4.183; 4.186. Дома: ОЛ-7 гл.4: № 4.152; 4.177; 4.174; 4.184. Занятие 13. Рубежный контроль по модулю 3. Модуль 4: Квадратичные формы Занятие 14. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования. Ауд.: ОЛ-7 гл.4: № 4.213; 4.214; 4.215. Дома: ОЛ-7 гл.4: № 4.216. Занятие 15. Приведение уравнения линии второго порядка и поверхности второго порядка к каноническому виду. Ауд.: ОЛ-7 гл.4: № 4.226; 4.228; 4.235; 4.237. Дома: ОЛ-7 гл.4: № 4.227; 4.229; 4.233; 4.239. Занятие 16. Контрольная работа «Квадратичные формы». Занятие 17. Приведение квадратичной формы методом Лагранжа к нормальному виду. Знакоопределенность квадратичной формы. Ауд.: ОЛ-7 гл.4: № 4.210; 4.211; 4.218; 4.221; 4.223. Дома: ОЛ-7 гл.4: № 4.212; 4.219; 4.220; 4.224. Контрольные мероприятия Модуль 1: Матрицы и системы линейных алгебраических уравнений (5 неделя, максимум 16 баллов, минимум 8 баллов). Рубежный контроль по модулю 1 (5 неделя). Модуль 2: Линейные и евклидовы пространства (9 неделя, максимум 20 баллов, минимум 10 баллов). Домашнее задание №1 «Линейные и евклидовы пространства» (выдача 6 неделя, прием 9 неделя). Рубежный контроль по модулю 2 (9 неделя). Модуль 3: Линейные операторы (13 неделя, максимум 26 баллов, минимум 14 баллов). Рубежный контроль по модулю 2 (13 неделя). Модуль 4: Квадратичные формы (17 неделя, максимум 28 баллов, минимум 14 баллов) Домашнее задание №2 «Приложения квадратичных форм» (выдача 13 неделя, прием 17 неделя). Рубежный контроль по модулю 2 (17 неделя). Типовые задания Домашнее задание №1. «Линейные и евклидовы пространства» Модуль 2, литература МП-1, МП-2. Задача 1 (2 балла). В линейном пространстве Вариант: Задача 2 (4 балла). В евклидовом пространстве 1. Применяя процесс ортогонализации, построить по базису 2. Найти матрицу перехода от нового базиса 3. Найти координаты векторов 4. Вычислить скалярное произведение 5. Вычислить угол между векторами Вариант:
Домашнее задание №2 «Приложения квадратичных форм» Модуль 4, литература МП-1, МП-2, МП-3. Уравнение а) линии второго порядка на плоскости в системе координат 1) одно из преобразований перехода от заданной системы координат к канонической системе координат (собственные числа ортогонального преобразования расположить в порядке возрастания); 2) канонический вид уравнения линии и поверхности, значения всех параметров, характеризующих форму линии и поверхности; 3) на плоскости построить исходную систему координат 4) поверхность построить в канонической системе координат. Вариант: а) б)
|
||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.147 (0.011 с.) |

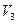 свободных векторов выбран правый ортонормированный базис
свободных векторов выбран правый ортонормированный базис 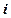 ,
, 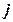 ,
, 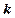 . Этот базис поворачивается вокруг заданного вектора
. Этот базис поворачивается вокруг заданного вектора 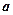 (это один из базисных векторов) на заданный угол
(это один из базисных векторов) на заданный угол 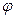 в указанном направлении (положительном или отрицательном), а затем вокруг вектора
в указанном направлении (положительном или отрицательном), а затем вокруг вектора 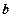 (один из базисных векторов в новом положении) на заданный угол
(один из базисных векторов в новом положении) на заданный угол 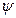 в указанном направлении. В результате получается новый базис
в указанном направлении. В результате получается новый базис 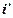 ,
,  ,
, 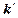 . Найти матрицу перехода из старого базиса в новый.
. Найти матрицу перехода из старого базиса в новый.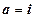 ,
,  ,
,  ,
, 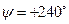 .
.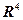 задан базис
задан базис 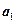 ,
, 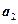 ,
, 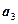 ,
,  (координаты этих векторов определены в стандартном базисе) и два вектора
(координаты этих векторов определены в стандартном базисе) и два вектора  и
и  (их координаты определены в заданном базисе
(их координаты определены в заданном базисе  ).
).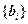 .
.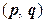 .
.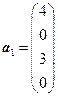 ,
, 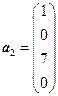 ,
,  ,
, 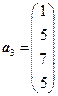 ,
, 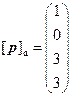 ,
, 
 и уравнения б) поверхности второго порядка в пространстве в системе координат
и уравнения б) поверхности второго порядка в пространстве в системе координат  привести к каноническому виду, указав:
привести к каноническому виду, указав: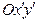 , эскиз линии; для центральной линии найти координаты центра, вершин, фокусов, уравнения асимптот (для гиперболы), а для параболы — координаты вершины, фокуса, уравнение директрисы;
, эскиз линии; для центральной линии найти координаты центра, вершин, фокусов, уравнения асимптот (для гиперболы), а для параболы — координаты вершины, фокуса, уравнение директрисы;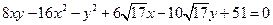 ; — 4 балла
; — 4 балла .— 6 баллов
.— 6 баллов


