Решение линейных систем с помощью обратной матрицы
Если ввести одностолбцовые матрицы неизвестных
 = = 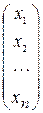 и свободных членов и свободных членов 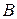 =, то =, то 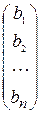 система (1), с учетом действий над матрицами, примет вид система (1), с учетом действий над матрицами, примет вид
 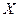 = = 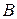 . (2) . (2)
Равенство (2) называют матричной формой записи линейной системы (1). Если определитель системы (1) D = det  ¹ 0, то матрица ¹ 0, то матрица  системы имеет обратную матрицу системы имеет обратную матрицу 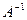 . У множив матричное равенство (2) слева на . У множив матричное равенство (2) слева на 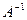 , получим равенство или (так как, , получим равенство или (так как, 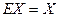 ). Следовательно, столбец неизвестных равен произведению ). Следовательно, столбец неизвестных равен произведению 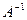 на столбец свободных членов. на столбец свободных членов.
Пример. Решить систему 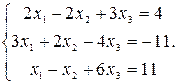
Матрица системы 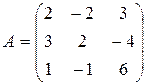 , а её определитель , а её определитель
det  = 24 + 8 –9 – 6 +36 – 8 = 45. = 24 + 8 –9 – 6 +36 – 8 = 45.
Найдем обратную матрицу 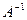 . .
Имеем 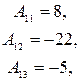 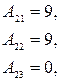 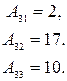
Следовательно, 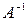 = = 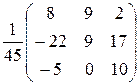 , а столбец неизвестных , а столбец неизвестных 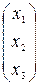 = = = = 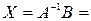 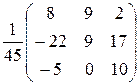 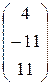 = = 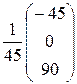 = = 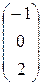 . .
Таким образом, числа 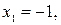 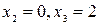 являются решением данной системы. являются решением данной системы.
Задание 3. Метод Гаусса. Пусть дана система m уравнений с n неизвестными общего вида
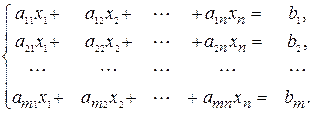 (3) (3)
Для практического отыскания решений общих линейных систем чаще всего используется метод Гаусса. Этот метод состоит из следующих трех этапов:
1. Записываем расширенную матрицу 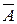 системы (3) и сверху над каждым столбцом записываем неизвестные, из коэффициентов при которых образован этот столбец системы (3) и сверху над каждым столбцом записываем неизвестные, из коэффициентов при которых образован этот столбец
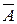 = = 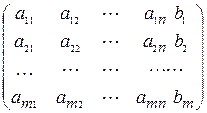 . .
2.Приводим расширенную матрицу 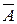 системы (3) к трапецевидной форме с матрицей системы (3) к трапецевидной форме с матрицей 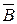 . Для этого применяются элементарные преобразования матрицы . Для этого применяются элементарные преобразования матрицы 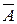 следующего вида а) перестановка местами двух строк матрицы следующего вида а) перестановка местами двух строк матрицы 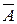 ; б) умножение строки матрицы на число, отличное от нуля; в) прибавление к одной строке матрицы другой строки; г) перестановка местами столбцов матрицы ; б) умножение строки матрицы на число, отличное от нуля; в) прибавление к одной строке матрицы другой строки; г) перестановка местами столбцов матрицы  вместе с неизвестными. Элементарные преобразования а), б), в) над строками расширенной матрицы вместе с неизвестными. Элементарные преобразования а), б), в) над строками расширенной матрицы 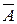 системы соответствуют следующие преобразования самой системы (3): перестановка местами двух строк расширенной матрицы системы эквивалентна перестановке местами двух соответствующих уравнений этой системы; умножение строки матрицы на число, отличное от 0, эквивалентно умножению соответствующего уравнения системы (3) на это число; прибавление к одной строке матрицы другой строки эквивалентно сложению двух соответствующих уравнений системы. Следовательно, матрица системы соответствуют следующие преобразования самой системы (3): перестановка местами двух строк расширенной матрицы системы эквивалентна перестановке местами двух соответствующих уравнений этой системы; умножение строки матрицы на число, отличное от 0, эквивалентно умножению соответствующего уравнения системы (3) на это число; прибавление к одной строке матрицы другой строки эквивалентно сложению двух соответствующих уравнений системы. Следовательно, матрица 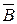 , полученная из матрицы , полученная из матрицы 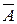 указанными преобразованиями, является расширенной матрицей системы, эквивалентной исходной системе. указанными преобразованиями, является расширенной матрицей системы, эквивалентной исходной системе.
3. При этом возможны три случая: а) система имеет единственное решение, б) система имеет бесконечно много решений, в) система несовместна (не имеет решений). Рассмотрим все эти случаи на конкретных примерах.
Пример 1. Решить методом Гаусса систему
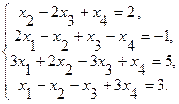
Приведем расширенную матрицу системы к трапецевидной форме.
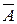 = = 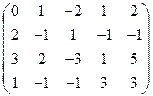 ® ® 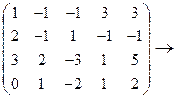 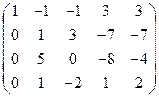 ® ®
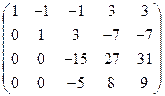 ® ® 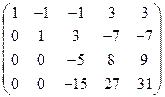 ®. ®.
Следовательно, ранг матрицы системы равен рангу расширенной матрицы и равен числу неизвестных, а поэтому система имеет единственное решение. Из последней строки матрицы находим 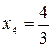 (так как (так как 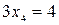 ), из третьей строки получаем ), из третьей строки получаем 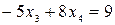 или или 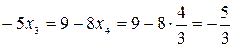 , а , а 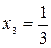 ; из второй строки получаем уравнение ; из второй строки получаем уравнение 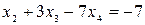 и находим и находим 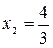 ; наконец из первой строки получаем ; наконец из первой строки получаем 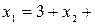 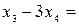 = = 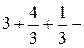 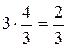 . .
Следовательно, 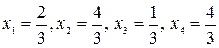 есть единственное решение данной системы. Чтобы убедиться в правильности решения сделаем проверку, то есть подставим найденное решение в каждое уравнение системы: есть единственное решение данной системы. Чтобы убедиться в правильности решения сделаем проверку, то есть подставим найденное решение в каждое уравнение системы:
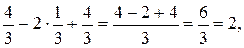 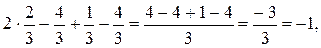 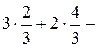 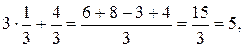 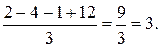
Пример 2. Решить систему методом Гаусса
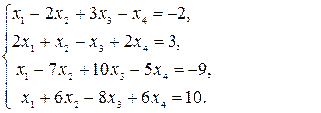
Приведем расширенную матрицу системы к трапецевидной форме:
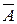 = ® ® ® →= = ® ® ® →= 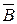 . .
Данная система имеет бесконечное множество решений, так как из третьей строки матрицы 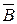 получаем получаем 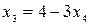 . .
Из второй строки получаем уравнение  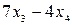 = = 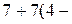 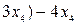 или. Из первой строки матрицы получаем, или. Из первой строки матрицы получаем, 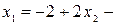 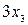 + + + + 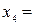  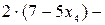 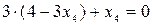 . .
Обозначив 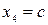 , запишем множество всех решений системы , запишем множество всех решений системы
 , ,
где 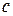 – любое действительное число. – любое действительное число.
Пример 3. Решить систему
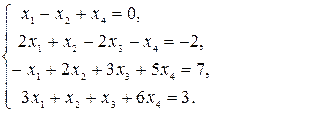
Приводим расширенную матрицу системы к трапецевидной форме:
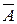 = ® ® ® = ® ® ® 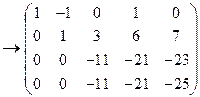 ®. ®.
Из последнего уравнения полученной матрицы имеем 0 = –2, что невозможно. Значит, рассматриваемая система несовместна.
Задание 4. Разберём порядок выполнения этого задания на примере векторов 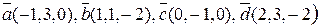 . .
Векторы 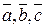 компланарны (образуют базис в пространстве) компланарны (образуют базис в пространстве) 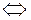 смешанное произведение этих векторов отлично от нуля. Вычислим смешанное произведение смешанное произведение этих векторов отлично от нуля. Вычислим смешанное произведение 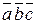 = = 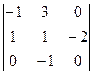 = 0 + 0 + 0 – 0 – 0 + 2 = 2 ≠ 0. = 0 + 0 + 0 – 0 – 0 + 2 = 2 ≠ 0.
Следовательно, данные векторы образуют базис. Координаты 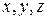 вектора вектора 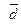 в базисе в базисе 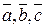 определяются равенством определяются равенством 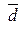 = =  + + 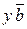 + + 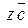 . Подставив в это равенство декартовы координаты векторов . Подставив в это равенство декартовы координаты векторов 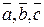 , , 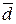 , получим векторное равенство , получим векторное равенство 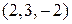 = = 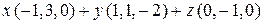 = = 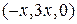 + + + + 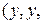 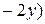 + + 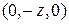 = = 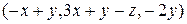 . .
Приравнивая соответствующие координаты векторов в левой и правой частях последнего равенства, получим линейную систему для определения координат вектора 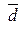 . .
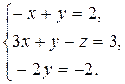
Из последнего уравнения системы находим 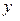 = 1, из первого уравнения получим = 1, из первого уравнения получим 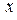 = – 1, = – 1, 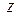 = – 1. = – 1.
Следовательно, в базисе 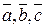 вектор вектор 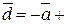 + + 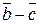 . .
Единичный орт вектора получается делением каждой координаты этого вектора на его длину, то есть 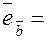 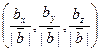 . В нашем случае длина вектора . В нашем случае длина вектора 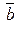 = = 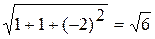 . .
Следовательно, единичный орт вектора 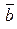 равен равен 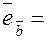 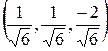 . Проекцию вектора . Проекцию вектора 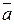 на вектор на вектор 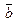 найдем по формуле найдем по формуле 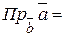 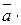 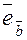 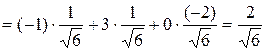 (проекция вектора (проекция вектора 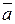 на вектор на вектор 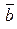 равна скалярному произведению вектора равна скалярному произведению вектора 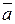 на единичный орт вектора на единичный орт вектора 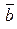 ). ).
Косинус угла α между векторами 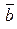 и и 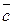 находим из определения скалярного произведения находим из определения скалярного произведения 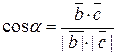 = =  = = = = 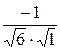 = = 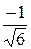 . .
Следовательно, 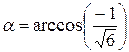 . .
Площадь параллелограмма, построенного на векторах 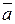 и и 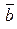 , равна модулю векторного произведения этих векторов , равна модулю векторного произведения этих векторов 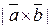 . Вычислим сначала векторное произведение этих векторов по формуле . Вычислим сначала векторное произведение этих векторов по формуле
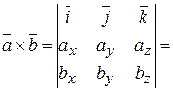 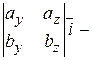 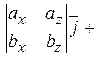 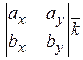 = = 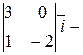
– 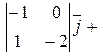 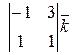 = = 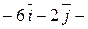  . Найдём теперь площадь параллелограмма . Найдём теперь площадь параллелограмма 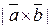 = = 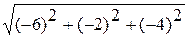 = = 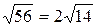 . Объём параллелепипеда, построенного на векторах . Объём параллелепипеда, построенного на векторах 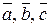 равен модулю смешанного произведения этих векторов, то есть V равен модулю смешанного произведения этих векторов, то есть V 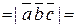 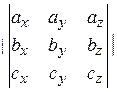 = 2. = 2.
Следовательно, V = 2.
Задание 5. Условимся называть 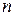 – мерными векторами или просто векторами одностолбцовые матрицы вида – мерными векторами или просто векторами одностолбцовые матрицы вида  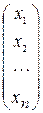 . Пусть дана квадратная матрица . Пусть дана квадратная матрица  порядка порядка 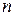 . .
Определение. Число 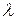 называется собственным числом матрицы называется собственным числом матрицы  , если существует отличный от нуля вектор , если существует отличный от нуля вектор  (хотя бы одно число (хотя бы одно число 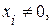 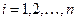 ) такой, что выполняется равенство ) такой, что выполняется равенство
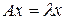 , (4) , (4)
а вектор 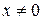 называется собственным вектором матрицы называется собственным вектором матрицы  , соответствующим собственному числу , соответствующим собственному числу 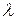 . .
Из определения собственных чисел и собственных векторов следует практический способ их отыскания. Действительно, преобразуем равенство (4) следующим способом: 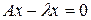 или или 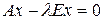 (так как (так как 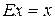 ) или ) или
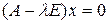 , (5) , (5)
где 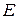 – единичная матрица порядка – единичная матрица порядка 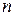 . Равенство (5) является матричной формой записи линейной однородной системы . Равенство (5) является матричной формой записи линейной однородной системы
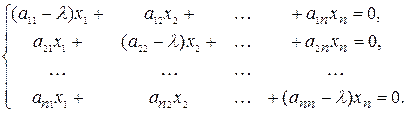 (6) (6)
Известно, что однородная система (6) имеет ненулевое решение тогда, и только тогда, когда её определитель равен нулю. Следовательно, матрица  имеет собственные числа и собственные векторы тогда и только тогда, когда имеет собственные числа и собственные векторы тогда и только тогда, когда
det 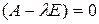 . (7) . (7)
Равенство (7), которое является алгебраическим уравнением степени 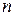 , называется характеристическим уравнением для матрицы , называется характеристическим уравнением для матрицы  . .
Из сказанного выше следует, что число 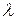 является собственным числом матрицы является собственным числом матрицы  тогда и только тогда, когда тогда и только тогда, когда 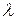 есть корень характеристического уравнения (7). А вектор есть корень характеристического уравнения (7). А вектор  – собственный вектор матрицы – собственный вектор матрицы  , соответствующий собственному числу , соответствующий собственному числу 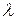 , тогда и только тогда, когда , тогда и только тогда, когда 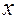 является решением линейной однородной системы (5) для этого является решением линейной однородной системы (5) для этого 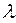 . .
Пример. Найти собственные числа и собственные векторы матрицы
 = = 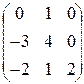 . Составим характеристическое уравнение det . Составим характеристическое уравнение det 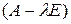 = = = = 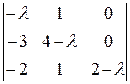 = (2 - = (2 - 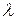 )×[ )×[ 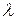 ( (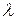 - 4) + 3 ] = (2 - - 4) + 3 ] = (2 - 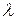 )( )(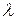 - 4 - 4 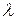 + 3) = 0. + 3) = 0.
Следовательно, 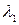 =2, =2, 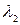 = 3, = 3, 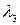 = 1 есть собственные числа данной матрицы. Теперь для каждого собственного числа найдем соответствующие им собственные векторы. = 1 есть собственные числа данной матрицы. Теперь для каждого собственного числа найдем соответствующие им собственные векторы.
1) Для 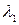 =2 система (6) имеет вид =2 система (6) имеет вид 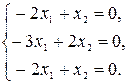 (подставили (подставили 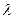 = 2). Расширенная матрица этой системы равна = 2). Расширенная матрица этой системы равна 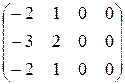 ® ® 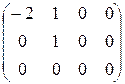 . Использованы следующие преобразования: из третьей строки вычли первую строку; из второй строки, умноженной на 2, вычли первую строку, умноженную на 3. Из последней матрицы следует, . Использованы следующие преобразования: из третьей строки вычли первую строку; из второй строки, умноженной на 2, вычли первую строку, умноженную на 3. Из последней матрицы следует, 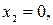 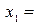 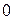 а неизвестная а неизвестная 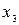 может принимать любые значения. Обозначив может принимать любые значения. Обозначив 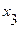 = = 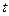 , запишем множество всех собственных векторов, соответствующих собственному числу , запишем множество всех собственных векторов, соответствующих собственному числу 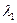 = 2, в виде = 2, в виде  где где 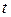 – любое действительное число, отличное от 0. – любое действительное число, отличное от 0.
2). Для 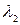 = 3 система (6) имеет вид = 3 система (6) имеет вид 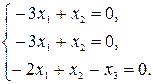
Преобразуем расширенную матрицу этой системы  = = 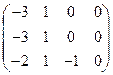 ® ® 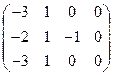 ® ® 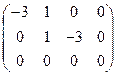 . .
Из второй строки последней матрицы находим 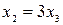 , а из первой строки следует, что , а из первой строки следует, что 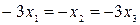 или или 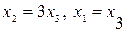 . .
Следовательно, собственные векторы, соответствующие этому собственному числу, имеют вид 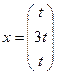  где где 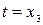 – любое действительное число. – любое действительное число.
3) Для 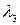 = 1 система (6) имеет вид = 1 система (6) имеет вид 
а расширенная матрица этой системы
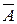 = = 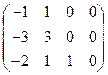 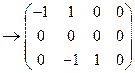 ® ® 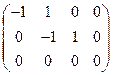 . .
Отсюда находим 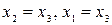 . .
Следовательно, искомые собственные векторы 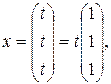 где где 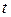 – любое действительное число, отличное от 0. – любое действительное число, отличное от 0.
Задание 6. Пусть точки пространства  (–2, 3, 1), (–2, 3, 1), 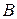 (0, –4, –1), а плоскость P имеет уравнение (0, –4, –1), а плоскость P имеет уравнение 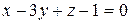 . .
1. Обозначим 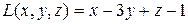 . Если . Если  , то есть числа , то есть числа 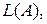 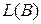 одного знака, тогда точки одного знака, тогда точки  и и 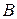 лежат в одном полупространстве относительно плоскости P. Если же лежат в одном полупространстве относительно плоскости P. Если же 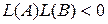 , то эти точки расположены в разных полупространствах относительно плоскости P. , то эти точки расположены в разных полупространствах относительно плоскости P.
Имеем: 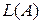 = = 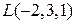 = = 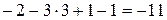 , , 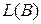 = = 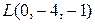 = = = = 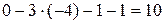 . Следовательно, . Следовательно, 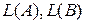 разных знаков, а точки разных знаков, а точки  , , 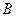 лежат в разных полупространствах относительно плоскости P. лежат в разных полупространствах относительно плоскости P.
2. Длину отрезка 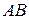 найдём по формуле найдём по формуле
| 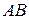 | = = | = = 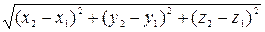 = = 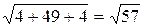 ; ;
расстояние от точки 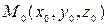 до плоскости P определяется равенством до плоскости P определяется равенством 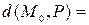 = = 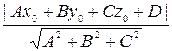 . .
Следовательно, расстояние от точки  до плоскости P равно до плоскости P равно
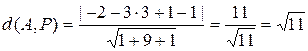 . .
3. Вектор 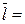 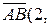 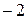 , , 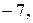 ) является направляющим вектором прямой ) является направляющим вектором прямой 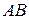 . Следовательно, каноническое уравнение прямой . Следовательно, каноническое уравнение прямой 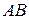 (уравнение прямой, проходящей через точку (уравнение прямой, проходящей через точку  и имеющей данный направляющий вектор) имеет вид и имеющей данный направляющий вектор) имеет вид

Чтобы найти точку пересечения прямой 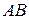 с плоскостью P перейдем к параметрическому уравнению этой прямой, введя параметр с плоскостью P перейдем к параметрическому уравнению этой прямой, введя параметр 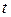 равенством равенством
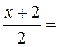 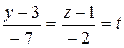 . Выразив из последнего равенства . Выразив из последнего равенства 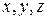 через через 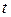 : :  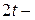 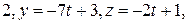 и подставив эти значения в уравнение плоскости, получим равенство и подставив эти значения в уравнение плоскости, получим равенство 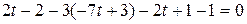 . Из этого уравнения находим . Из этого уравнения находим 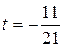 , а из параметрического уравнения прямой определяем координаты точки пересечения прямой и плоскости , а из параметрического уравнения прямой определяем координаты точки пересечения прямой и плоскости 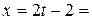 = = 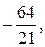 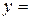  3 = 3 = 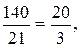 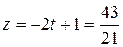 . .
Следовательно, точка пересечения имеет координаты 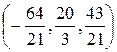 . .
Синус угла между прямой и плоскостью определяется следующим равенством
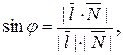
где 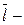 направляющий вектор прямой, направляющий вектор прямой, 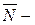 нормальный вектор плоскости, а нормальный вектор плоскости, а 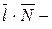 скалярное произведение этих векторов. В нашем случае скалярное произведение этих векторов. В нашем случае 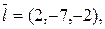 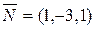 , , 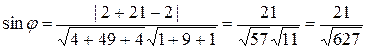 . .
4. Так как прямая должна быть перпендикулярна плоскости P, то нормаль к плоскости будет направляющим вектором искомой прямой, то есть 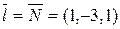 . Каноническое уравнение искомой прямой имеет вид . Каноническое уравнение искомой прямой имеет вид 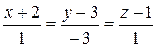 . Точка . Точка  (–2, 3, 1) принадлежит этой прямой. (–2, 3, 1) принадлежит этой прямой.
Следовательно, расстояние от точки 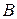 (0,–4,–1) до прямой равно площади параллелограмма, построенного на векторах (0,–4,–1) до прямой равно площади параллелограмма, построенного на векторах 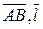 , делённой на , делённой на 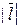 (длину основания). Таким образом, искомое расстояние (длину основания). Таким образом, искомое расстояние 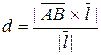 . Векторное произведение векторов . Векторное произведение векторов 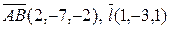 равно равно 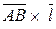 = = 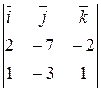 = =  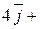 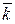 . .
Следовательно, 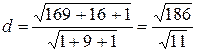 . .
5. Проекцией точки  на плоскость P является основание перпендикуляра, опущенного из точки на плоскость P является основание перпендикуляра, опущенного из точки  на плоскость P. Уравнение этого перпендикуляра было составлено в предыдущем пункте и имеет вид на плоскость P. Уравнение этого перпендикуляра было составлено в предыдущем пункте и имеет вид 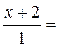 = = 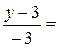 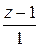 . Найдём точку пересечения этого перпендикуляра с плоскостью P. Для этого перейдём к параметрическому уравнению . Найдём точку пересечения этого перпендикуляра с плоскостью P. Для этого перейдём к параметрическому уравнению 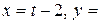 = = 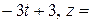 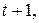 и подставим в уравнение плоскости и подставим в уравнение плоскости 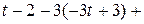 + + 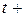 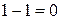 . .
Получаем, 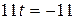 или или 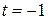 , а координаты проекции , а координаты проекции  точки точки  на плоскость P равны на плоскость P равны  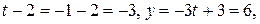 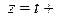 + + 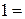 0. 0.
Следовательно, 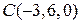 есть проекция точки есть проекция точки  на плоскость P. Пусть точка на плоскость P. Пусть точка 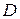 симметрична точке симметрична точке  относительно плоскости P. Следовательно, точка относительно плоскости P. Следовательно, точка 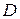 принадлежит перпендикуляру принадлежит перпендикуляру 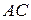 и | и | 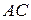 | = | | = | 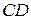 |. Вектор |. Вектор 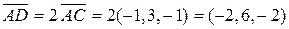 , а координаты точки , а координаты точки 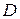 равны сумме соответствующих координат точки равны сумме соответствующих координат точки  и вектора и вектора 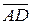 , то есть , то есть 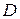 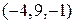 . .
Задание 7. При выполнении этого задания необходимо учесть связь декартовых координат точки с полярными координатами этой точки: 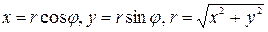 . Пусть, например, уравнение линии в полярных координатах имеет вид . Пусть, например, уравнение линии в полярных координатах имеет вид 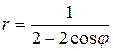 . Умножив это уравнение на . Умножив это уравнение на 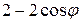 , получим равенство , получим равенство 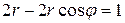 , которое в декартовых прямоугольных координатах примет вид , которое в декартовых прямоугольных координатах примет вид 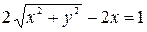 или или 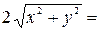 = = 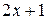 . Возводя последнее равенство в квадрат, получим . Возводя последнее равенство в квадрат, получим 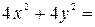 = = 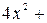 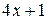 или или 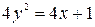 . Поделив последнее равенство на 4, получаем каноническое уравнение параболы . Поделив последнее равенство на 4, получаем каноническое уравнение параболы 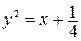 с вершиной в точке с вершиной в точке 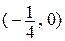 . .
Задание 8. 1) Если требуется вычислить предел при 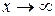 функции, являющейся частным двух полиномов, то говорят, что имеется неопределённость вида функции, являющейся частным двух полиномов, то говорят, что имеется неопределённость вида 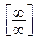 . Для раскрытия этой неопределённости необходимо поделить числитель и знаменатель дроби на старшую степень . Для раскрытия этой неопределённости необходимо поделить числитель и знаменатель дроби на старшую степень  . .
Пример. Вычислим 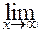 = = 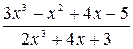 = = 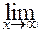 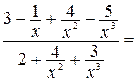
= 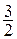 , так как дроби , так как дроби 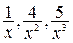 стремятся к нулю при стремятся к нулю при 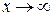 , а старшей степенью переменной , а старшей степенью переменной  является является 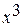 . .
Пример. Вычислим 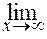 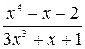 = = 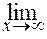 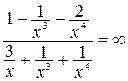 , так как старшей степенью переменной , так как старшей степенью переменной  является является 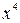 , а после деления числителя и знаменателя дроби на , а после деления числителя и знаменателя дроби на 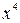 , числитель стремится к 1, а знаменатель к 0. , числитель стремится к 1, а знаменатель к 0.
2. Если требуется вычислить предел при 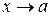 ( ( – число) функции, являющейся частным двух полиномов, а числитель и знаменатель одновременно стремятся к 0, то говорят, что имеется неопределённость вида – число) функции, являющейся частным двух полиномов, а числитель и знаменатель одновременно стремятся к 0, то говорят, что имеется неопределённость вида 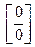 . Для раскрытия этой неопределённости необходимо разложить числитель и знаменатель дроби на множители и сократить . Для раскрытия этой неопределённости необходимо разложить числитель и знаменатель дроби на множители и сократить  . .
Пример.
   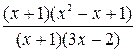 = =   = = = =  . .
3. Если числитель или знаменатель дроби содержит выражение вида  , то для раскрытия неопределённости необходимо числитель и знаменатель дроби умножить на сопряжённое , то для раскрытия неопределённости необходимо числитель и знаменатель дроби умножить на сопряжённое  . .
Пример.
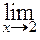  = =  = =  = =
=   = =   == ==   = =  . .
4. Вычисление пределов функции с помощью замечательных пределов: а) 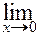  , б) , б) 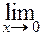  в) в)   , ,
г)    д) д) 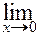 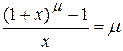 . .
Пример. Вычислим предел   с использованием первого с использованием первого
замечательного предела а). Имеем 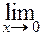  = =   = = = =    8 8   8 8  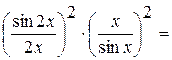
= 
Пример. Пусть требуется вычислить 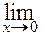  . Для этого используем замечательные пределы в) и г). Имеем, . Для этого используем замечательные пределы в) и г). Имеем,   = = = =  = (так как = (так как  при при  ) = ) =  = = = =  = =  = =  = = = =  . .
Пример. Для вычисления  воспользуемся замечательными пределами а) и д). воспользуемся замечательными пределами а) и д).
Действительно,  = = = =  = = = =  = = = =   . .
Обозначим  при при  . .
Тогда получим 2   = 2 = 2  = = = = 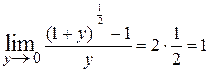 , так как , так как  = 1. = 1.
Если требуется вычислить  а а  , ,  = =  тогда говорят, что имеет место неопределённость типа тогда говорят, что имеет место неопределённость типа  . Для раскрытия такой неопределённости используется замечательный предел б). . Для раскрытия такой неопределённости используется замечательный предел б).
Пример. Вычислим  . Так как . Так как  = 1, а 1– = 1, а 1–  при при 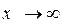 , ,
то имеет место не
|



 =
= 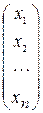 и свободных членов
и свободных членов  =, то
=, то 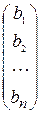 система (1), с учетом действий над матрицами, примет вид
система (1), с учетом действий над матрицами, примет вид
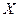 =
= 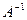 . У множив матричное равенство (2) слева на
. У множив матричное равенство (2) слева на 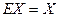 ). Следовательно, столбец неизвестных равен произведению
). Следовательно, столбец неизвестных равен произведению 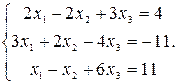
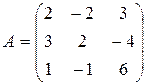 , а её определитель
, а её определитель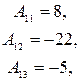
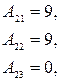
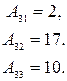
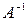 =
= 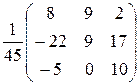 , а столбец неизвестных
, а столбец неизвестных 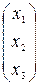 = =
= = 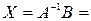
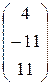 =
= 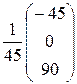 =
= 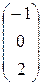 .
.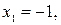
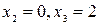 являются решением данной системы.
являются решением данной системы.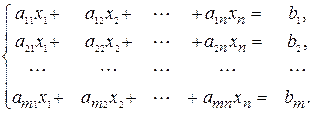 (3)
(3)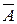 системы (3) и сверху над каждым столбцом записываем неизвестные, из коэффициентов при которых образован этот столбец
системы (3) и сверху над каждым столбцом записываем неизвестные, из коэффициентов при которых образован этот столбец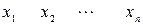
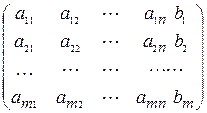 .
.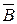 . Для этого применяются элементарные преобразования матрицы
. Для этого применяются элементарные преобразования матрицы  вместе с неизвестными. Элементарные преобразования а), б), в) над строками расширенной матрицы
вместе с неизвестными. Элементарные преобразования а), б), в) над строками расширенной матрицы 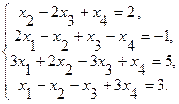
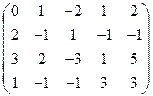 ®
® 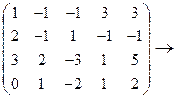
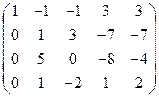 ®
®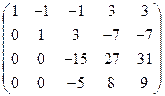 ®
® 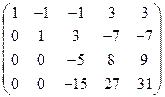 ®.
®.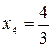 (так как
(так как 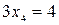 ), из третьей строки получаем
), из третьей строки получаем 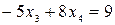 или
или 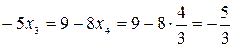 , а
, а 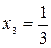 ; из второй строки получаем уравнение
; из второй строки получаем уравнение 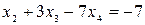 и находим
и находим 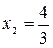 ; наконец из первой строки получаем
; наконец из первой строки получаем 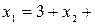
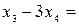 =
= 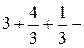
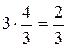 .
.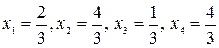 есть единственное решение данной системы. Чтобы убедиться в правильности решения сделаем проверку, то есть подставим найденное решение в каждое уравнение системы:
есть единственное решение данной системы. Чтобы убедиться в правильности решения сделаем проверку, то есть подставим найденное решение в каждое уравнение системы: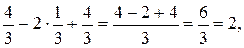
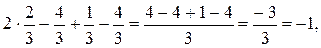
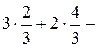
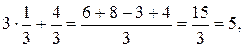
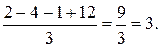
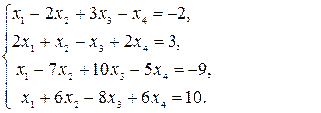
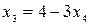 .
.
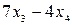 =
= 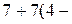
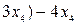 или. Из первой строки матрицы получаем,
или. Из первой строки матрицы получаем, 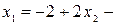
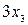 + +
+ + 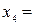

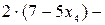
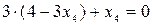 .
.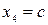 , запишем множество всех решений системы
, запишем множество всех решений системы ,
,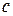 – любое действительное число.
– любое действительное число.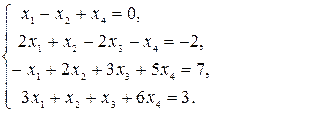
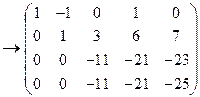 ®.
®.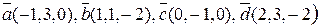 .
.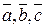 компланарны (образуют базис в пространстве)
компланарны (образуют базис в пространстве) 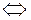 смешанное произведение этих векторов отлично от нуля. Вычислим смешанное произведение
смешанное произведение этих векторов отлично от нуля. Вычислим смешанное произведение 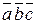 =
= 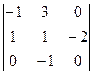 = 0 + 0 + 0 – 0 – 0 + 2 = 2 ≠ 0.
= 0 + 0 + 0 – 0 – 0 + 2 = 2 ≠ 0.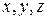 вектора
вектора 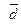 в базисе
в базисе 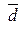 =
=  +
+ 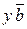 +
+ 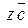 . Подставив в это равенство декартовы координаты векторов
. Подставив в это равенство декартовы координаты векторов 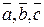 ,
, 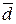 , получим векторное равенство
, получим векторное равенство 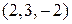 =
= 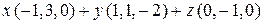 =
= 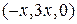 + +
+ + 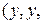
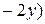 +
+ 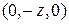 =
= 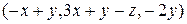 .
.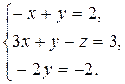
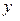 = 1, из первого уравнения получим
= 1, из первого уравнения получим 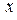 = – 1,
= – 1, 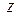 = – 1.
= – 1.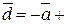 +
+ 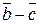 .
.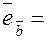
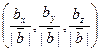 . В нашем случае длина вектора
. В нашем случае длина вектора 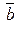 =
= 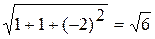 .
.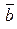 равен
равен 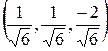 . Проекцию вектора
. Проекцию вектора 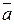 на вектор
на вектор 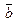 найдем по формуле
найдем по формуле 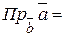
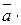
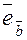
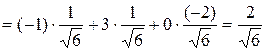 (проекция вектора
(проекция вектора 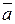 на вектор
на вектор 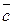 находим из определения скалярного произведения
находим из определения скалярного произведения 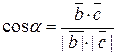 =
=  = =
= = 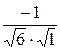 =
= 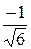 .
.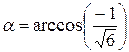 .
.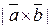 . Вычислим сначала векторное произведение этих векторов по формуле
. Вычислим сначала векторное произведение этих векторов по формуле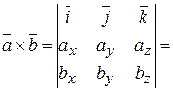
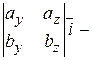
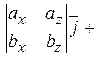
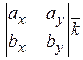 =
= 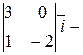
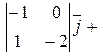
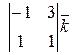 =
= 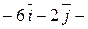
 . Найдём теперь площадь параллелограмма
. Найдём теперь площадь параллелограмма 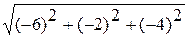 =
= 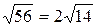 . Объём параллелепипеда, построенного на векторах
. Объём параллелепипеда, построенного на векторах 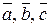 равен модулю смешанного произведения этих векторов, то есть V
равен модулю смешанного произведения этих векторов, то есть V 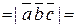
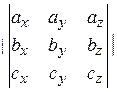 = 2.
= 2.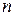 – мерными векторами или просто векторами одностолбцовые матрицы вида
– мерными векторами или просто векторами одностолбцовые матрицы вида 
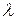 называется собственным числом матрицы
называется собственным числом матрицы  (хотя бы одно число
(хотя бы одно число 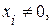
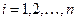 ) такой, что выполняется равенство
) такой, что выполняется равенство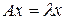 , (4)
, (4)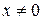 называется собственным вектором матрицы
называется собственным вектором матрицы 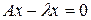 или
или 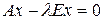 (так как
(так как 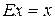 ) или
) или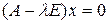 , (5)
, (5)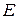 – единичная матрица порядка
– единичная матрица порядка 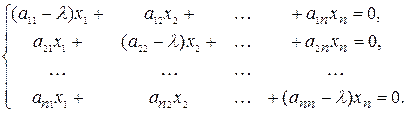 (6)
(6)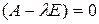 . (7)
. (7)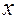 является решением линейной однородной системы (5) для этого
является решением линейной однородной системы (5) для этого 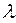 .
.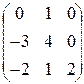 . Составим характеристическое уравнение det
. Составим характеристическое уравнение det 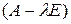 = =
= = 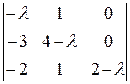 = (2 -
= (2 - 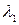 =2,
=2, 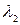 = 3,
= 3, 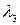 = 1 есть собственные числа данной матрицы. Теперь для каждого собственного числа найдем соответствующие им собственные векторы.
= 1 есть собственные числа данной матрицы. Теперь для каждого собственного числа найдем соответствующие им собственные векторы.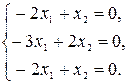 (подставили
(подставили 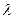 = 2). Расширенная матрица этой системы равна
= 2). Расширенная матрица этой системы равна 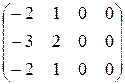 ®
® 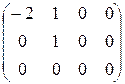 . Использованы следующие преобразования: из третьей строки вычли первую строку; из второй строки, умноженной на 2, вычли первую строку, умноженную на 3. Из последней матрицы следует,
. Использованы следующие преобразования: из третьей строки вычли первую строку; из второй строки, умноженной на 2, вычли первую строку, умноженную на 3. Из последней матрицы следует, 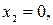
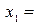
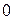 а неизвестная
а неизвестная 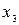 может принимать любые значения. Обозначив
может принимать любые значения. Обозначив 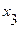 =
= 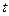 , запишем множество всех собственных векторов, соответствующих собственному числу
, запишем множество всех собственных векторов, соответствующих собственному числу 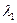 = 2, в виде
= 2, в виде  где
где 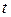 – любое действительное число, отличное от 0.
– любое действительное число, отличное от 0.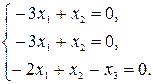
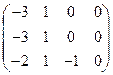 ®
® 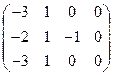 ®
® 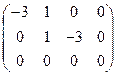 .
.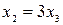 , а из первой строки следует, что
, а из первой строки следует, что 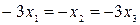 или
или 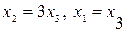 .
.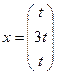
 где
где 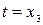 – любое действительное число.
– любое действительное число.
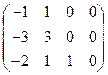
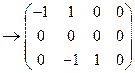 ®
® 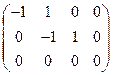 .
.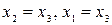 .
.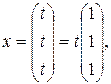 где
где 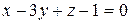 .
.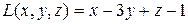 . Если
. Если  , то есть числа
, то есть числа 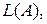
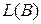 одного знака, тогда точки
одного знака, тогда точки 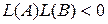 , то эти точки расположены в разных полупространствах относительно плоскости P.
, то эти точки расположены в разных полупространствах относительно плоскости P.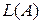 =
= 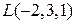 =
= 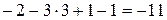 ,
, 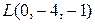 = =
= = 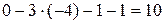 . Следовательно,
. Следовательно, 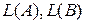 разных знаков, а точки
разных знаков, а точки  лежат в разных полупространствах относительно плоскости P.
лежат в разных полупространствах относительно плоскости P. найдём по формуле
найдём по формуле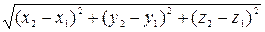 =
= 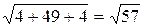 ;
;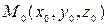 до плоскости P определяется равенством
до плоскости P определяется равенством 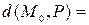 =
= 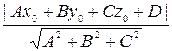 .
.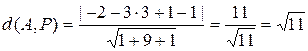 .
.
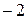 ,
, 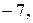 ) является направляющим вектором прямой
) является направляющим вектором прямой 
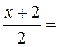
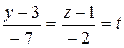 . Выразив из последнего равенства
. Выразив из последнего равенства 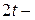
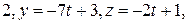 и подставив эти значения в уравнение плоскости, получим равенство
и подставив эти значения в уравнение плоскости, получим равенство 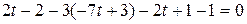 . Из этого уравнения находим
. Из этого уравнения находим 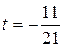 , а из параметрического уравнения прямой определяем координаты точки пересечения прямой и плоскости
, а из параметрического уравнения прямой определяем координаты точки пересечения прямой и плоскости 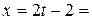 =
= 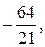
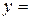
 3 =
3 = 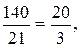
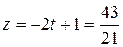 .
.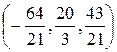 .
.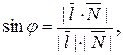
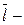 направляющий вектор прямой,
направляющий вектор прямой, 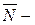 нормальный вектор плоскости, а
нормальный вектор плоскости, а 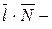 скалярное произведение этих векторов. В нашем случае
скалярное произведение этих векторов. В нашем случае 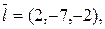
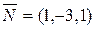 ,
, 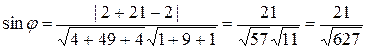 .
.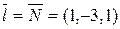 . Каноническое уравнение искомой прямой имеет вид
. Каноническое уравнение искомой прямой имеет вид 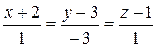 . Точка
. Точка 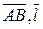 , делённой на
, делённой на 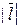 (длину основания). Таким образом, искомое расстояние
(длину основания). Таким образом, искомое расстояние 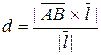 . Векторное произведение векторов
. Векторное произведение векторов 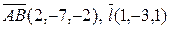 равно
равно 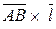 =
= 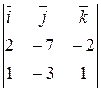 =
= 
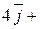
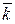 .
.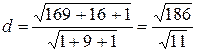 .
.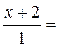 =
= 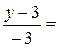
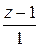 . Найдём точку пересечения этого перпендикуляра с плоскостью P. Для этого перейдём к параметрическому уравнению
. Найдём точку пересечения этого перпендикуляра с плоскостью P. Для этого перейдём к параметрическому уравнению 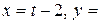 =
= 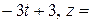
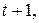 и подставим в уравнение плоскости
и подставим в уравнение плоскости 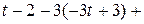 +
+ 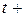
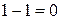 .
.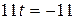 или
или 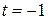 , а координаты проекции
, а координаты проекции 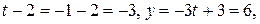
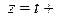 +
+ 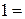 0.
0.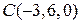 есть проекция точки
есть проекция точки 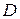 симметрична точке
симметрична точке 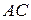 и |
и |  |. Вектор
|. Вектор 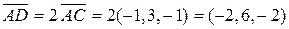 , а координаты точки
, а координаты точки 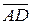 , то есть
, то есть 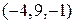 .
.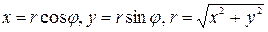 . Пусть, например, уравнение линии в полярных координатах имеет вид
. Пусть, например, уравнение линии в полярных координатах имеет вид 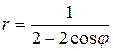 . Умножив это уравнение на
. Умножив это уравнение на 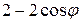 , получим равенство
, получим равенство 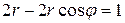 , которое в декартовых прямоугольных координатах примет вид
, которое в декартовых прямоугольных координатах примет вид 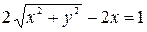 или
или 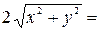 =
= 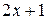 . Возводя последнее равенство в квадрат, получим
. Возводя последнее равенство в квадрат, получим 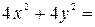 =
= 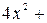
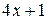 или
или 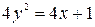 . Поделив последнее равенство на 4, получаем каноническое уравнение параболы
. Поделив последнее равенство на 4, получаем каноническое уравнение параболы 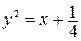 с вершиной в точке
с вершиной в точке 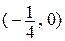 .
.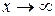 функции, являющейся частным двух полиномов, то говорят, что имеется неопределённость вида
функции, являющейся частным двух полиномов, то говорят, что имеется неопределённость вида 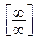 . Для раскрытия этой неопределённости необходимо поделить числитель и знаменатель дроби на старшую степень
. Для раскрытия этой неопределённости необходимо поделить числитель и знаменатель дроби на старшую степень 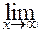 =
= 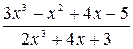 =
= 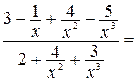
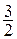 , так как дроби
, так как дроби 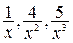 стремятся к нулю при
стремятся к нулю при 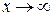 , а старшей степенью переменной
, а старшей степенью переменной 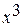 .
.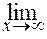
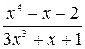 =
= 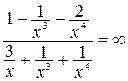 , так как старшей степенью переменной
, так как старшей степенью переменной 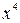 , а после деления числителя и знаменателя дроби на
, а после деления числителя и знаменателя дроби на 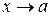 (
( – число) функции, являющейся частным двух полиномов, а числитель и знаменатель одновременно стремятся к 0, то говорят, что имеется неопределённость вида
– число) функции, являющейся частным двух полиномов, а числитель и знаменатель одновременно стремятся к 0, то говорят, что имеется неопределённость вида 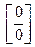 . Для раскрытия этой неопределённости необходимо разложить числитель и знаменатель дроби на множители и сократить
. Для раскрытия этой неопределённости необходимо разложить числитель и знаменатель дроби на множители и сократить  .
.


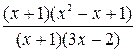 =
=  = =
= =  .
. , то для раскрытия неопределённости необходимо числитель и знаменатель дроби умножить на сопряжённое
, то для раскрытия неопределённости необходимо числитель и знаменатель дроби умножить на сопряжённое  .
.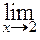
 =
=  =
=  =
= =
=  ==
== 
 =
=  .
.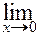
 , б)
, б) 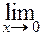
 в)
в) 
 ,
,
 д)
д) 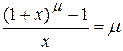 .
. с использованием первого
с использованием первого = =
= = 
 8
8 
 8
8 
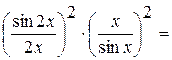

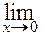
 . Для этого используем замечательные пределы в) и г). Имеем,
. Для этого используем замечательные пределы в) и г). Имеем, 
 = =
= =  = (так как
= (так как  при
при  ) =
) =  = =
= =  =
=  =
=  = =
= =  .
. воспользуемся замечательными пределами а) и д).
воспользуемся замечательными пределами а) и д). = =
= =  = =
= = 
 .
. при
при 
 = 2
= 2  = =
= = 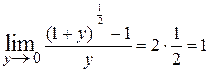 , так как
, так как  а
а  ,
,  =
=  тогда говорят, что имеет место неопределённость типа
тогда говорят, что имеет место неопределённость типа  . Для раскрытия такой неопределённости используется замечательный предел б).
. Для раскрытия такой неопределённости используется замечательный предел б). . Так как
. Так как  = 1, а 1–
= 1, а 1–  при
при 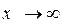 ,
,


