
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к контрольной работе 1Содержание книги
Поиск на нашем сайте
ВЫСШАЯ МАТЕМАТИКА
ВЕЛИКИЙ НОВГОРОД Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Новгородский государственный университет имени Ярослава Мудрого»
ВЫСШАЯ МАТЕМАТИКА Методические указания и контрольные задания для студентов заочного сокращенного обучения Часть 1 ВЕЛИКИЙ НОВГОРОД УДК 51(075.8) Печатается по решению ББК 22.1я73 РИС НовГУ В93
Рецензент
доктор физико–математических наук, профессор Е. Ю. Панов
Высшая математика: методические указания и контрольные задания для студентов заочного сокращенного обучения.Ч1.- 2-е изд., исп. и доп. /авт.-сост. О.Н. Барсов; ФГБОУ ВПО «Новгородский государственный университет им. Ярослава Мудрого», Великий Новгород, 2011. – 76с.
Пособие содержит задания для контрольных работ за первый семестр и методические указания к их выполнению по курсу высшей математики для студентов ускоренной формы обучения заочного отделения инженерно–технических специальностей.
УДК 51(075.8) ББК 22.1я73
© ФГБОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого», 2011 © О.Н. Барсов, составление, 2011 ВВЕДЕНИЕ
Курс высшей математики для студентов ускоренной формы обучения (на базе среднего специального образования) рассчитан на два семестра. В каждом семестре студентам необходимо выполнить две контрольных работы, каждая из которых содержит восемь заданий. Каждая контрольная работа содержит десять вариантов контрольных заданий с номерами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Номер варианта контрольной работы соответствует последней цифре номера зачетной книжки студента. Например, студент, у которого последней цифрой номера зачетной книжки является цифра 3, выполняет третий вариант всех четырех контрольных работ. Контрольные работы должны быть оформлены в соответствии с нижеизложенными правилами: 1) каждую контрольную работу следует выполнять в отдельной тетради (12 листов) чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента; 2) на обложке тетради должны быть ясно написаны фамилия и инициалы студента, шифр, номер контрольной работы и название дисциплины; необходимо также, указать дату отсылки работы в университет и адрес студента; в конце работы следует проставить дату выполнения и расписаться;
3) должны быть выполнены все задания своего варианта (работы, содержащие не все задания, а также содержащие задания другого варианта, не засчитываются); 4) задачи в работе надо располагать в порядке возрастания номеров, сохраняя нумерацию; 5) перед решением каждой задачи нужно выписать полностью её условие, подставляя конкретные данные из своего варианта; решение задач следует излагать подробно, объясняя все действия по ходу решения и делая необходимые чертежи; 6) рекомендуется оставлять в конце тетради чистые листы для исправлений и дополнений в соответствии с указаниями рецензента (вносить исправления в сам текст работы после её рецензирования запрещается); 7) после получения не зачтённой, прорецензированной работы (зачтённые работы остаются у рецензента), студент должен исправить все указанные рецензентом ошибки и недочёты в той же тетради после слов работа над ошибками; 8) к экзамену допускаются только те студенты, контрольные работы которых зачтены рецензентом; так как на рецензирование контрольной работы преподавателю отводится две недели, то задания следует высылать на проверку заблаговременно. ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ 1
Задание 8. Вычислите указанные пределы, не пользуясь правилом Лопиталя. 6. а) г)
Задание 9. Исследовать данные функции на непрерывность. Если у функции функции в этих точках (точка разрыва первого или второго рода).
6. а) Задание 10. Найдите производные второго порядка 6. а) ОПРЕДЕЛИТЕЛИ Каждой квадратной матрице ставится в соответствие действительное число, которое вычисляется по определённым правилам по элементам матрицы. Это число называют определителем (детерминантом) матрицы
Если матрица Минором Алгебраическим дополнением элемента Определителем квадратной матрицы
1. Определитель второго порядка
Например,
Обратная матрица Обратной к квадратной матрице Матрицу обратную к матрице ления следует единственность обратной матрицы. Действительно, если Теорема. Квадратная матрица
где
Пример. Найдём Пример. Найдём Следовательно, Проверка:
Задание 2. Рассмотрим линейную неоднородную систему n уравнений с n неизвестными
Вместе с определителем D системы будем рассматривать определители D D =
Теорема 2 (Крамера). Система (1) имеет единственное решение Û определитель системы D ¹ 0. При этом, решение системы определяется формулами Крамера: Пример. Решить по теореме Крамера следующую систему:
Определитель системы Следовательно, рассматриваемая система имеет единственное решение. Вычислим определители D Имеем = Таким образом,
Пример.
3. Если числитель или знаменатель дроби содержит выражение вида Пример.
= 4. Вычисление пределов функции с помощью замечательных пределов: а) г) Пример. Вычислим предел замечательного предела а). Имеем = Пример. Пусть требуется вычислить Пример. Для вычисления
Действительно, Обозначим Тогда получим 2
Если требуется вычислить
Пример. Вычислим то имеет место неопределённость типа Далее, Обозначим
Тогда
Задание 9. Это контрольное задание относится к теме: «Непрерывность функции, точки разрыва и их классификация». Рассмотрим основные понятия, относящиеся к этой теме. Определение. Функция Если функция Определение. Точка Из определения точки разрыва следует, что если
Из определения также следует, что Определение. Точка Определение. Точка Пример. Функция
Следовательно, точка Пример. Проверим непрерывность этой функции в точке
Следовательно, точка
Пример. = +∞. Так как правосторонний предел точкой разрыва второго рода. Выделим теперь основной класс непрерывных функций. Справедливо утверждение, что все элементарные функции (степенная Перечислим основные свойства непрерывных функций. Пусть функции Тогда: 1) функция C
Из непрерывности основных элементарных функций и свойств непрерывных функций следует, что сумма, произведение и частное двух элементарных функций непрерывна в своей области определения. Например, функция Пример. Исследовать на непрерывность функцию
Отметим, что во всех точках, кроме точек Следовательно, Следовательно,
Задание 10. Это задание относится к теме: «Дифференциальное исчисление функции одной переменной». Основным понятием этой темы является понятие производной функции. Определение. Производной функции Разность Вычислим производную функции
Из определения производной функции и замечательных пределов получают производные основных элементарных функций.
Таблица производных основных элементарных функций
1.
2. 3. 4. 5. | |||||||
|
| Поделиться: |

 , б)
, б) 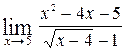 , в)
, в)  ,
, ;
; имеются точки разрыва, тогда определить характер разрыва
имеются точки разрыва, тогда определить характер разрыва
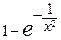 , б)
, б) 
 функций, первая из которых задана уравнением
функций, первая из которых задана уравнением  , вторая неявно, а третья параметрически.
, вторая неявно, а третья параметрически. =
=  , б)
, б) 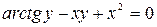 , в)
, в) 
 ,
,  .
. и обозначают det
и обозначают det 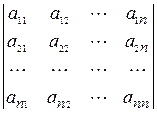 .
. , то определитель такой матрицы считают равным этому числу, т.е. det
, то определитель такой матрицы считают равным этому числу, т.е. det  . Далее будем считать, что порядок матрицы
. Далее будем считать, что порядок матрицы 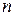 > 1.
> 1.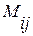 элемента
элемента  матрицы
матрицы  является определитель
является определитель  .
. матрицы
матрицы  =
=  . Из определения видно, что алгебраическое дополнение
. Из определения видно, что алгебраическое дополнение 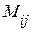 , если i+j – чётное число, и
, если i+j – чётное число, и  =
=  =
= 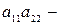
 .
. =
=  .
.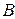 такую, что
такую, что  , где
, где 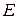 – единичная матрица.
– единичная матрица. . Из опреде-
. Из опреде- являются обратными к матрице
являются обратными к матрице  , тогда
, тогда  . Отсюда имеем
. Отсюда имеем  .
. ,
, матрицы
матрицы  ,
, 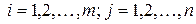 .
. . det
. det 
 . Следовательно,
. Следовательно,  . Проверка:
. Проверка: 
 .
. . Имеем, det
. Имеем, det  =
= 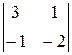
 =
= 

 –1,
–1, 

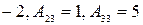 .
. =
= 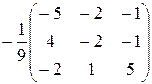 .
. .
. (1)
(1)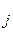 , получающиеся из определителя D заменой
, получающиеся из определителя D заменой  – того столбца столбцом свободных членов, т. е.
– того столбца столбцом свободных членов, т. е. .
. .
.
 = –10 – 40 –21 –8– 30 +35 = – 74 ¹ 0.
= –10 – 40 –21 –8– 30 +35 = – 74 ¹ 0. .
. = 40 + 50 – 14 + 10 – 20 – 140 = –74,
= 40 + 50 – 14 + 10 – 20 – 140 = –74,  = –10 – 80 –15 – 8 – 60 +25 = –148,
= –10 – 80 –15 – 8 – 60 +25 = –148,  = –10 –16 + 84 +32 –30 + +14 = 74.
= –10 –16 + 84 +32 –30 + +14 = 74.
 =
=  – решение данной системы.
– решение данной системы.


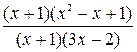 =
=  = =
= =  .
. , то для раскрытия неопределённости необходимо числитель и знаменатель дроби умножить на сопряжённое
, то для раскрытия неопределённости необходимо числитель и знаменатель дроби умножить на сопряжённое  .
.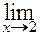
 =
=  =
=  =
= =
=  ==
== 
 =
=  .
.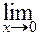
 , б)
, б) 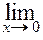
 в)
в) 
 ,
,
 д)
д) 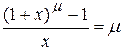 .
. с использованием первого
с использованием первого = =
= = 
 8
8 
 8
8 
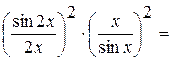

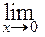
 . Для этого используем замечательные пределы в) и г). Имеем,
. Для этого используем замечательные пределы в) и г). Имеем, 
 = =
= =  = (так как
= (так как  при
при  ) =
) =  = =
= =  =
=  =
=  = =
= =  .
. воспользуемся замечательными пределами а) и д).
воспользуемся замечательными пределами а) и д). = =
= =  = =
= = 
 .
. при
при 
 = 2
= 2  = =
= = 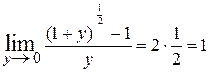 , так как
, так как  а
а  ,
,  =
=  тогда говорят, что имеет место неопределённость типа
тогда говорят, что имеет место неопределённость типа  . Для раскрытия такой неопределённости используется замечательный предел б).
. Для раскрытия такой неопределённости используется замечательный предел б). . Так как
. Так как  = 1, а 1–
= 1, а 1–  при
при 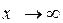 ,
, = 1 +
= 1 +  .
. при
при 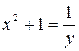 , а
, а  . Данный предел примет вид
. Данный предел примет вид  =1+ аат место неопределённо (
=1+ аат место неопределённо ( =
=  =
=  , так как
, так как 
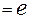 .
. называется непрерывной в точке
называется непрерывной в точке  , если: 1)
, если: 1)  (то есть можно вычислить значения функции для всех значений
(то есть можно вычислить значения функции для всех значений 
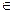 (
(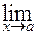
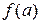 .
. не определена в точке
не определена в точке  ,
, 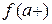 и, по определению,
и, по определению, 

 не определена в точке
не определена в точке 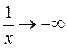 , а
, а  , если
, если 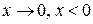 , то имеем
, то имеем  =
= 

 = 1. Аналогично, так как
= 1. Аналогично, так как  , а
, а 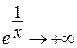 , если
, если 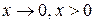 , то
, то  = =
= = 

 =1, тогда, по теореме об односторонних пределах, существуют односторонние пределы
=1, тогда, по теореме об односторонних пределах, существуют односторонние пределы 
 .
. . Рассматриваемая функция не определена в точке
. Рассматриваемая функция не определена в точке  , показательная
, показательная  , логарифмическая
, логарифмическая  ,
,  ,
, 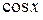 ,
, 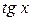 ,
,  ,
,  ,
,  ,
,  ,
,  ) непрерывны в своей области определения. Например, функция
) непрерывны в своей области определения. Например, функция 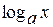 определена на множестве (0, +∞), а значит и непрерывна на этом множестве.
определена на множестве (0, +∞), а значит и непрерывна на этом множестве. непрерывны в точке
непрерывны в точке  непрерывна в точке
непрерывна в точке  ≠ 0; 5) непрерывность суперпозиции двух функций (сложной функции): если функция
≠ 0; 5) непрерывность суперпозиции двух функций (сложной функции): если функция  непрерывна в точке
непрерывна в точке  = =
= =  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , тогда функция
, тогда функция 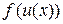 непрерывна в точке
непрерывна в точке  непрерывна на множестве (0, +∞); функция
непрерывна на множестве (0, +∞); функция  непрерывна в своей области определения (0,+∞) как частное двух элементарных функций. Функция
непрерывна в своей области определения (0,+∞) как частное двух элементарных функций. Функция 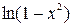 определена на промежутке (–1, 1), а значит и непрерывна на этом промежутке.
определена на промежутке (–1, 1), а значит и непрерывна на этом промежутке.
 для
для  для
для  =
= 
 = 1,
= 1,  =
= 

 = 1,
= 1,  = 2 ─ 1= 1.
= 2 ─ 1= 1. =
= 
 = –1,
= –1,  =
= 
 = 1, а
= 1, а  = 2 – 3= –1.
= 2 – 3= –1. называется число
называется число  =
=  , если этот предел существует; если в точке
, если этот предел существует; если в точке  называют приращением функции, соответствующим приращению аргумента
называют приращением функции, соответствующим приращению аргумента 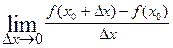 .
. в точке
в точке  =
=  =
=  = =
= =  =
=  =
=  .
. =
=  (производная степенной функции);
(производная степенной функции);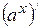 =
=  (производная показательной функции), в частности
(производная показательной функции), в частности  =
= 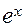 ;
; = =
= =  (производная логарифмической функции), в частности
(производная логарифмической функции), в частности  =
= 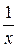 ;
; =
= 


