Методические указания к контрольной работе 2
Задание 1. Это задание относится к теме: «Исследование функции с помощью производной и построение её графика». Для того чтобы построить график функции  необходимо провести исследование основных свойств этой функции по следующей схеме: необходимо провести исследование основных свойств этой функции по следующей схеме:
1) найти область определения D(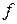 ) функции ) функции  ; ;
2) найти точки пересечения графика функции с координатными осями;
3) выяснить, является ли функция  чётной или нечётной; чётной или нечётной;
4) выяснить, является ли функция  периодической или нет; периодической или нет;
5) найти интервалы возрастания (убывания) функции и точки локального экстремума;
6) найти интервалы выпуклости вверх (вниз) и точки перегиба функции;
7) найти вертикальные и наклонные асимптоты кривой  (графика функции (графика функции  ); исследовать поведение функции на границах области определения D( ); исследовать поведение функции на границах области определения D(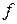 ) (например, область определения логарифмической функции D( ) (например, область определения логарифмической функции D( ) = (0, +∞); на границе ) = (0, +∞); на границе  = 0 области определения поведение функции определится в пункте 7), так как прямая = 0 области определения поведение функции определится в пункте 7), так как прямая  = 0 является вертикальной асимптотой и = 0 является вертикальной асимптотой и 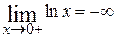 , а на границе +∞ необходимо вычислить , а на границе +∞ необходимо вычислить  + ∞). + ∞).
Остановимся подробнее на каждом выше указанном пункте схемы.
1. Областью определения функции  называют множество всех значений аргумента называют множество всех значений аргумента  , для которых можно выполнить все указанные в функции действия над аргументом. Область определения функции , для которых можно выполнить все указанные в функции действия над аргументом. Область определения функции  принято обозначать D( принято обозначать D(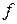 ). Например, область определения функции ). Например, область определения функции  определяется системой неравенств определяется системой неравенств  + 1 ≠ 0, + 1 ≠ 0,  . Эти неравенства эквивалентны неравенствам . Эти неравенства эквивалентны неравенствам  либо либо  После объединения решений двух последних систем неравенств получим, что D( После объединения решений двух последних систем неравенств получим, что D(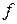 ) = ) =
= (– ∞, –1)  [0, + ∞). [0, + ∞).
2. Точка пересечения графика функции  с осью OY (осью ординат) имеет координаты (0, с осью OY (осью ординат) имеет координаты (0,  ). Чтобы найти точку пересечения графика с осью OX (осью абсцисс) необходимо решить уравнение ). Чтобы найти точку пересечения графика с осью OX (осью абсцисс) необходимо решить уравнение  = 0; если точка = 0; если точка  – решение этого уравнения, то есть – решение этого уравнения, то есть  = 0, тогда точка с координатами ( = 0, тогда точка с координатами ( ,0) является точкой пересечения графика функции с осью OX. ,0) является точкой пересечения графика функции с осью OX.
Если уравнение  = 0 имеет несколько решений = 0 имеет несколько решений 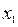 , ,  , ,  , ,  , тогда точки , тогда точки  , ,  , ,  , ,  будут точками пересечения графика с осью OX. Найдём, например, точки пересечения графика функции будут точками пересечения графика с осью OX. Найдём, например, точки пересечения графика функции  = =  с координатными осями. Так как с координатными осями. Так как  = 2, тогда точка пересечения с осью OY имеет координаты (0,2). Для определения точек пересечения графика с осью OX решим уравнение = 2, тогда точка пересечения с осью OY имеет координаты (0,2). Для определения точек пересечения графика с осью OX решим уравнение  = 0, которое эквивалентно квадратному уравнению = 0, которое эквивалентно квадратному уравнению  , имеющему два решения , имеющему два решения  = 1, = 1,  = 2. = 2.
Следовательно, график рассматриваемой функции пересекает ось OX в двух точках с координатами (1,0), (2,0).
3. Определение. Функция  называется чётной, если для любых значений аргумента называется чётной, если для любых значений аргумента  , принадлежащих области определения D( , принадлежащих области определения D(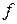 ), выполняется равенство ), выполняется равенство  = =  ; если же для любых ; если же для любых  D( D(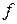 ) выполняется равенство ) выполняется равенство  = = 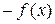 , тогда функция , тогда функция  называется нечётной. называется нечётной.
Области определения чётной и нечётной функций должны быть симметричны относительно точки  = 0, так как вместе с точкой = 0, так как вместе с точкой  множеству D( множеству D(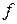 ) принадлежит и точка – ) принадлежит и точка –  . Например, функции . Например, функции  , ,  являются чётными, так как для них выполняется равенство являются чётными, так как для них выполняется равенство  = =  , а функции , а функции  являются нечётными, так как для них выполняется равенство являются нечётными, так как для них выполняется равенство  = = 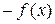 . .
Очевидно, что произведение двух нечётных функций является чётной функцией, а произведение чётной функции на нечётную является функцией нечётной.
Например, функция  является чётной, так как получена умножением двух нечётных функций, а функция является чётной, так как получена умножением двух нечётных функций, а функция  является нечётной как произведение чётной и нечётной функций. Функция является нечётной как произведение чётной и нечётной функций. Функция  не является ни чётной, ни нечётной функцией, так как её область определения D( не является ни чётной, ни нечётной функцией, так как её область определения D( ) = (0, +∞) не симметрична относительно начала координат. ) = (0, +∞) не симметрична относительно начала координат.
Свойства чётности и нечётности функции при построении графиков функций используются следующим образом: график чётной функции симметричен относительно оси OY, а график нечётной функции симметричен относительно начала координат.
Следовательно, достаточно построить график таких функций для
 ≥ 0, а затем отобразить симметрично относительно оси OY (для чётной функции) либо относительно начала координат (для нечётной функции). ≥ 0, а затем отобразить симметрично относительно оси OY (для чётной функции) либо относительно начала координат (для нечётной функции).
4. Определение. Функция  называется периодической с периодом называется периодической с периодом 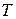 , если для всех , если для всех  D( D(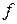 ) выполняется равенство ) выполняется равенство 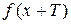 = =  . .
Очевидно, что если число 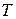 является периодом функции является периодом функции  , тогда числа , тогда числа 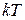 , где , где  = 0, ± 1, ± 2, = 0, ± 1, ± 2, 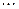 , также являются периодами этой функции. Основным периодом функции называют наименьший положительный период этой функции. , также являются периодами этой функции. Основным периодом функции называют наименьший положительный период этой функции.
Следовательно, основной период функций  , ,  , ,  равен 2 равен 2  , а основной период функций , а основной период функций   , , 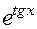 равен равен  . Отметим, что если основной период функции . Отметим, что если основной период функции  равен равен 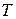 , тогда основной период функции , тогда основной период функции  будет равен будет равен  , где , где 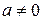 . .
Действительно,  = = = = 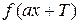 = =  . .
Следовательно, по определению периода,  будет основным периодом функции будет основным периодом функции 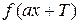 . Отсюда следует, что основным периодом функций . Отсюда следует, что основным периодом функций   будет число будет число  , а основной период функций , а основной период функций  буде равен буде равен  . .
Периодичность функции при построении графика учитывают следующим образом: строят график функции на промежутке  , или на любом другом промежутке длины , или на любом другом промежутке длины 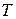 , а затем продолжают этот график по периоду на всю область определения. , а затем продолжают этот график по периоду на всю область определения.
5. Функция  называется монотонно возрастающей (монотонно убывающей) на интервале называется монотонно возрастающей (монотонно убывающей) на интервале 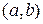 , если для любых , если для любых 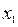 , ,  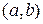 , таких что , таких что 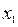 , ,  , выполняется неравенство , выполняется неравенство   ( (  ). ).
Для того чтобы функция  монотонно возрастала (монотонно убывала) на интервале монотонно возрастала (монотонно убывала) на интервале 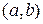 достаточно чтобы её производная достаточно чтобы её производная 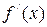 > 0 ( > 0 ( ) для всех значений ) для всех значений  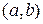 , за исключением конечного числа точек, в которых , за исключением конечного числа точек, в которых  . Например, функция . Например, функция  имеет производную имеет производную 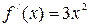 > 0 для всех > 0 для всех  , а , а  . Следовательно, эта функ- . Следовательно, эта функ-
ция монотонно возрастает на всей числовой прямой.
Определение. Точка  называется точкой локального максимума (локального минимума) функции называется точкой локального максимума (локального минимума) функции  , если существует число ∆ > 0 такое, что для любых значений , если существует число ∆ > 0 такое, что для любых значений  ( ( – ∆, – ∆,  + ∆) выполняется неравенство + ∆) выполняется неравенство   ( (  ). Точки локального максимума и локального минимума функции ). Точки локального максимума и локального минимума функции  называют точками экстремума этой функции. называют точками экстремума этой функции.
Необходимый признак экстремума. Если точка  является точкой экстремума функции является точкой экстремума функции  и существует производная и существует производная  , тогда , тогда  = = 0. = = 0.
Из необходимого признака экстремума следует, что у дифференцируемой функции точками экстремума могут быть только такие точки, в которых производная этой функции равна нулю. Такие точки называют стационарными точками функции.
Точками экстремума функции могут быть и такие точки, в которых  непрерывна, но не дифференцируема. Все точки этих двух типов, которые могут быть точками экстремума, называют критическими точками этой функции. непрерывна, но не дифференцируема. Все точки этих двух типов, которые могут быть точками экстремума, называют критическими точками этой функции.
Например, функция  = =  непрерывна для любых непрерывна для любых
 (– ∞, + ∞). Производная этой функции (– ∞, + ∞). Производная этой функции 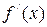 = = = =  . .
Решив уравнение 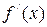 = 0, найдём единственную стационарную точку = 0, найдём единственную стационарную точку  . Но так как производная рассматриваемой функции не существует в точках . Но так как производная рассматриваемой функции не существует в точках  = ± 1 (в этих точках знаменатель дроби равен 0), то у функции, кроме стационарной точки = ± 1 (в этих точках знаменатель дроби равен 0), то у функции, кроме стационарной точки  , имеются две критических точки второго типа , имеются две критических точки второго типа  = ± 1. = ± 1.
Таким образом, для отыскания точек локального минимума и локального максимума функции сначала необходимо найти все критические точки этой функции. Так как не все критические точки в действительности являются точками экстремума функции, необходимо каждую из них проверить на наличие экстремума с помощью достаточных признаков экстремума. Рассмотрим два достаточных признака экстремума.
Первый достаточный признак экстремума. Пусть точка  является критической точкой является критической точкой  и существует производная и существует производная 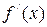 на множестве ( на множестве ( , ,  ) )  ( ( , ,  + ∆), где число ∆ > 0. + ∆), где число ∆ > 0.
1. Если 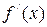 > 0 на промежутке ( > 0 на промежутке ( – ∆, – ∆,  ) и ) и 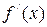 < 0 на промежутке ( < 0 на промежутке ( , ,  + ∆) (производная меняет знак с плюса на минус при переходе через точку + ∆) (производная меняет знак с плюса на минус при переходе через точку  ), тогда точка ), тогда точка  является точкой локального максимума является точкой локального максимума  . .
2. Если 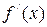 < 0 на промежутке ( < 0 на промежутке ( – –∆, – –∆,  ) и ) и 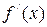 > 0 на промежутке (x > 0 на промежутке (x 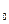 , x , x 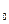 + ∆) (производная меняет знак с минуса на плюс при переходе через точку + ∆) (производная меняет знак с минуса на плюс при переходе через точку  ), тогда точка ), тогда точка  является точкой локального минимума является точкой локального минимума  . .
3. Если 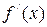 > 0 ( > 0 (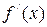 < 0) на множестве ( < 0) на множестве ( , ,  ) )  ( ( , ,  + ∆) (производная не меняет знак при переходе через точку + ∆) (производная не меняет знак при переходе через точку  ), тогда точка ), тогда точка  не является точкой экстремума. не является точкой экстремума.
Второй достаточный признак экстремума. Пусть точка  является стационарной точкой является стационарной точкой  (то есть (то есть  = 0). Тогда: 1) если = 0). Тогда: 1) если 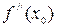 > 0, то точка > 0, то точка  является точкой локального минимума; 2) если является точкой локального минимума; 2) если 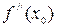 < 0, то точка < 0, то точка  является точкой локального максимума является точкой локального максимума  . .
Пример. Выше было установлено, что функция  = =  имеет три критических точки имеет три критических точки 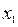 = – 1, = – 1,  = 0, = 0,  = 1. Для проверки этих точек на экстремум применим первый достаточный признак экстремума (второй признак не применим к точкам ± 1, так как в этих точках не существует производная = 1. Для проверки этих точек на экстремум применим первый достаточный признак экстремума (второй признак не применим к точкам ± 1, так как в этих точках не существует производная 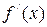 = =  ). Из выражения для производной видно, что знаменатель дроби ). Из выражения для производной видно, что знаменатель дроби  для всех значений для всех значений  , кроме , кроме  = ± 1. = ± 1.
Следовательно, производная меняет знак с минуса на плюс в точке  = 0 ( = 0 (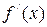 < 0 при < 0 при  < 0 и < 0 и 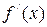 > 0 при > 0 при  > 0), и точка > 0), и точка  = 0 является точкой локального минимума. На промежутках (–∞,–1) = 0 является точкой локального минимума. На промежутках (–∞,–1)  (–1,0) производная отрицательна (функция монотонно убывает), а на промежутках (0,1) (–1,0) производная отрицательна (функция монотонно убывает), а на промежутках (0,1)  (1,+∞) производная положительна (функция монотонно возрастает). (1,+∞) производная положительна (функция монотонно возрастает).
Следовательно, производная не меняет знак при переходе через точки  = ± 1, а значит, эти точки не являются точками экстремума. = ± 1, а значит, эти точки не являются точками экстремума.
Так как точка  = 0 является стационарной, то для проверки этой точки на экстремум можно применить и второй достаточный признак экстремума. Действительно, = 0 является стационарной, то для проверки этой точки на экстремум можно применить и второй достаточный признак экстремума. Действительно,  = =  – –  , а , а  = =  > 0. > 0.
Следовательно, точка  = 0 является точкой локального минимума рассматриваемой функции. = 0 является точкой локального минимума рассматриваемой функции.
6. Определение. Кривая  называется выпуклой вверх (выпуклой вниз) на интервале называется выпуклой вверх (выпуклой вниз) на интервале 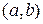 , если она расположена под касательной (над касательной), проведенной к этой кривой в любой точке , если она расположена под касательной (над касательной), проведенной к этой кривой в любой точке  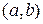 . .
Так как уравнение касательной к кривой  в точке в точке  имеет вид имеет вид 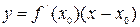 , то из определения следует, что кривая выпукла вверх на интервале , то из определения следует, что кривая выпукла вверх на интервале 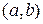 , если для любых , если для любых  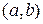 , ,  выполняется неравенство выполняется неравенство  < < < <  , и выпукла вниз на этом интервале, если , и выпукла вниз на этом интервале, если
выполняется противоположное неравенство  > >  . .
Справедливо следующее достаточное условие выпуклости вверх (вниз) на интервале: а) если  > 0 для любых > 0 для любых  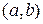 , тогда кривая , тогда кривая  выпукла вниз на выпукла вниз на 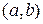 ; б) если ; б) если  < 0 для любых < 0 для любых  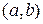 , то– , то–
гда кривая  выпукла вверх на интервале выпукла вверх на интервале 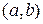 . .
Определение. Точка  , ,  ) называется точкой перегиба кривой ) называется точкой перегиба кривой 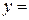  , если кривая меняет направление выпуклости в этой точке. То есть существует число ∆ > 0 такое, что на интервале ( , если кривая меняет направление выпуклости в этой точке. То есть существует число ∆ > 0 такое, что на интервале ( – ∆, – ∆,  ) кривая выпукла вверх (вниз), а на интервале ( ) кривая выпукла вверх (вниз), а на интервале ( , ,  + ∆) выпукла вниз (вверх). + ∆) выпукла вниз (вверх).
Необходимый признак точки перегиба. Если точка  , ,  ) кривой ) кривой  является точкой перегиба и существует является точкой перегиба и существует 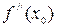 , тогда , тогда 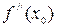 = 0. = 0.
Из необходимого признака следует, что точками перегиба кривой могут быть только точки, в которых 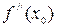 = 0 либо вторая производная не существует, а функция непрерывна. = 0 либо вторая производная не существует, а функция непрерывна.
Достаточный признак точки перегиба. 1). Если  < 0 ( < 0 ( > >
> 0) для всех  ( ( – ∆, – ∆,  ) и ) и  > 0 ( > 0 ( < 0) для всех < 0) для всех  ( ( , ,  + ∆), тогда точка + ∆), тогда точка  является точкой перегиба кривой. 2). Если является точкой перегиба кривой. 2). Если  < 0 ( < 0 ( > 0) для всех > 0) для всех  ( ( , ,  ) )  ( ( , ,  + ∆), тогда точка + ∆), тогда точка  не является точкой перегиба кривой не является точкой перегиба кривой  . .
Пример. Найдём точки перегиба кривой  . Находим, . Находим, 
=  = =  , а , а  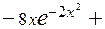   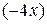 = =  = = 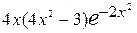 . .
Так как вторая производная существует для любых  , то точками перегиба могут быть только точки, в которых , то точками перегиба могут быть только точки, в которых  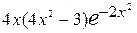 = 0. Последнее уравнение имеет три корня = 0. Последнее уравнение имеет три корня 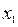 = =  , ,  = 0, = 0,  = =  . Так как . Так как  < 0 при < 0 при  (–∞, – (–∞, –  ), ),  > > 0 при > > 0 при  (– (–  , 0), , 0),  < 0 при < 0 при  (0, (0,  ), ),  > 0 при > 0 при  ( ( , +∞), то рассматриваемая кривая выпукла вверх на множестве (–∞,– , +∞), то рассматриваемая кривая выпукла вверх на множестве (–∞,–  ) )  (0, (0,  ) и выпукла вниз на множестве (– ) и выпукла вниз на множестве (–  , 0) , 0)  ( ( , +∞), а точки , +∞), а точки 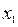 = ─ = ─  , ,  = 0, = 0,  = =  являются точками перегиба кривой. являются точками перегиба кривой.
7. Определение. Прямая линия  называется вертикальной асимптотой кривой называется вертикальной асимптотой кривой  (графика функции (графика функции  ), если хотя бы один из односторонних пределов ), если хотя бы один из односторонних пределов  , , 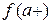 равен ∞. равен ∞.
Например, прямая  0 является вертикальной асимптотой кривой 0 является вертикальной асимптотой кривой  , так как правосторонний предел , так как правосторонний предел 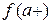 = = 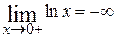 . .
Функция  = =  имеет две вертикальные асимптоты имеет две вертикальные асимптоты  ± 1, так как пределы ± 1, так как пределы  . Для более точного представления о поведении кривой при её приближении к асимптотам вычислим односторонние пределы. Имеем, предел слева . Для более точного представления о поведении кривой при её приближении к асимптотам вычислим односторонние пределы. Имеем, предел слева  = =  , предел справа , предел справа  = =  ; для вертикальной асимптоты ; для вертикальной асимптоты  1 левосторонний предел 1 левосторонний предел  = =  , а правосторонний предел , а правосторонний предел  = =  . .
Определение. Прямая линия 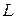 , заданная уравнением , заданная уравнением  , называется наклонной асимптотой кривой , называется наклонной асимптотой кривой  при при  (при (при  ), если расстояние от точки ), если расстояние от точки  этой кривой до прямой этой кривой до прямой 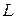 стремится к нулю ( стремится к нулю ( ) при ) при  (при (при  ). ).
В случае  , то есть асимптота имеет уравнение , то есть асимптота имеет уравнение  , её принято называть горизонтальной асимптотой. Отыскание наклонных асимптот основано на следующей теореме. , её принято называть горизонтальной асимптотой. Отыскание наклонных асимптот основано на следующей теореме.
Теорема. Прямая линия 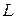 , заданная уравнением , заданная уравнением  , является наклонной асимптотой кривой , является наклонной асимптотой кривой  при при  (при (при  ) )  а) существует а) существует  (существует (существует   ), б) существует ), б) существует 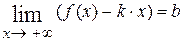 (существует (существует 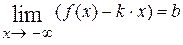 ). ).
Пример. Найдём наклонные асимптоты кривой  . Сначала ищется угловой коэффициент прямой . Сначала ищется угловой коэффициент прямой  = =  = = = =  = =  = 1. После того, как найден коэффициент k = =1, находим коэффициент = 1. После того, как найден коэффициент k = =1, находим коэффициент  = =  = = = =  = =  = 0. Вычисление коэффициентов = 0. Вычисление коэффициентов  асимптоты проведено при асимптоты проведено при  , так как вычисляемые пределы одинаковы как при , так как вычисляемые пределы одинаковы как при  , так и при , так и при  . Таким образом, рассматриваемая кривая имеет при . Таким образом, рассматриваемая кривая имеет при  и и  одну и туже наклонную асимптоту одну и туже наклонную асимптоту  . .
Задание 2. При вычислении пределов функций возникают семь типов неопределённостей  , , 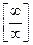 , [o∙∞], , [o∙∞],  , , 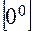 , ,  , [∞ ─ ∞]. Неопределённости первых двух типов возникают при вычислении пределов вида , [∞ ─ ∞]. Неопределённости первых двух типов возникают при вычислении пределов вида 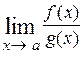 , когда числитель и знаменатель дроби одновременно стремятся к 0 или ∞, то есть , когда числитель и знаменатель дроби одновременно стремятся к 0 или ∞, то есть 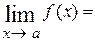  либо либо  = = = =  (возможно (возможно  = ∞). Такого рода неопределённости непосредственно раскрывает следующая теорема. = ∞). Такого рода неопределённости непосредственно раскрывает следующая теорема.
Теорема (Лопиталя). Пусть выполнены следующие условия:
1) функции  , ,  дифференцируемы на интервале дифференцируемы на интервале 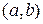 ; ;
2)  ≠ 0 на ≠ 0 на 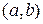 ; ;
3) 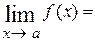  либо либо 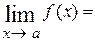  ; ;
4) существует 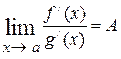 . .
Тогда существует  . .
Теорема сформулирована для случая левостороннего предела  , ,  . Утверждение этой теоремы остаётся верным и в случае правостороннего предела . Утверждение этой теоремы остаётся верным и в случае правостороннего предела  , ,  . Возможно также, что . Возможно также, что    . .
Пример. Вычислим  . Видно, что . Видно, что 
= 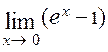 = 0. = 0.
Следовательно,  = =  = =  = – 1. = – 1.
Пример. Вычислим  . Применив правило Лопиталя (числитель и знаменатель дроби стремятся к +∞ при . Применив правило Лопиталя (числитель и знаменатель дроби стремятся к +∞ при  ), получим ), получим
 = = 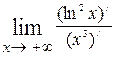 = = 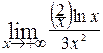 = =  = =  = 0. = 0.
Раскрытие неопределённости [o∙∞]. Такого рода неопределённость возникает при вычислении предела вида  , когда , когда 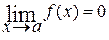 , ,  . В этом случае исходный предел преобразуют к одному из двух видов . В этом случае исходный предел преобразуют к одному из двух видов  либо либо 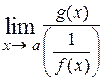 . В первом случае . В первом случае  и и  при x → a (неопределённость типа при x → a (неопределённость типа  ), а во втором случае ), а во втором случае  и и  при при  (неопределённость типа (неопределённость типа 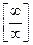 ). Затем, применяя правило Лопиталя, получают ). Затем, применяя правило Лопиталя, получают  = =  = = = =  либо либо  = = 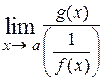 = = 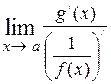 . .
Пример. Вычислим  . Так как . Так как  , а , а  , то имеем неопределённость типа [o∙∞]. Здесь удобнее отпра , то имеем неопределённость типа [o∙∞]. Здесь удобнее отпра
|



 необходимо провести исследование основных свойств этой функции по следующей схеме:
необходимо провести исследование основных свойств этой функции по следующей схеме: ) функции
) функции  (графика функции
(графика функции  ) = (0, +∞); на границе
) = (0, +∞); на границе  = 0 области определения поведение функции определится в пункте 7), так как прямая
= 0 области определения поведение функции определится в пункте 7), так как прямая 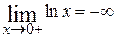 , а на границе +∞ необходимо вычислить
, а на границе +∞ необходимо вычислить  + ∞).
+ ∞). , для которых можно выполнить все указанные в функции действия над аргументом. Область определения функции
, для которых можно выполнить все указанные в функции действия над аргументом. Область определения функции  определяется системой неравенств
определяется системой неравенств  . Эти неравенства эквивалентны неравенствам
. Эти неравенства эквивалентны неравенствам  либо
либо  После объединения решений двух последних систем неравенств получим, что D(
После объединения решений двух последних систем неравенств получим, что D( [0, + ∞).
[0, + ∞). ). Чтобы найти точку пересечения графика с осью OX (осью абсцисс) необходимо решить уравнение
). Чтобы найти точку пересечения графика с осью OX (осью абсцисс) необходимо решить уравнение  – решение этого уравнения, то есть
– решение этого уравнения, то есть  = 0, тогда точка с координатами (
= 0, тогда точка с координатами (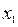 ,
,  ,
,  ,
,  , тогда точки
, тогда точки  ,
,  ,
,  будут точками пересечения графика с осью OX. Найдём, например, точки пересечения графика функции
будут точками пересечения графика с осью OX. Найдём, например, точки пересечения графика функции  с координатными осями. Так как
с координатными осями. Так как  , имеющему два решения
, имеющему два решения  ; если же для любых
; если же для любых  D(
D(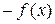 , тогда функция
, тогда функция  = 0, так как вместе с точкой
= 0, так как вместе с точкой  ,
,  являются чётными, так как для них выполняется равенство
являются чётными, так как для них выполняется равенство  являются нечётными, так как для них выполняется равенство
являются нечётными, так как для них выполняется равенство  является чётной, так как получена умножением двух нечётных функций, а функция
является чётной, так как получена умножением двух нечётных функций, а функция  является нечётной как произведение чётной и нечётной функций. Функция
является нечётной как произведение чётной и нечётной функций. Функция 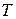 , если для всех
, если для всех 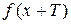 =
= 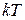 , где
, где  = 0, ± 1, ± 2,
= 0, ± 1, ± 2,  ,
,  ,
,  равен 2
равен 2  , а основной период функций
, а основной период функций 
 ,
, 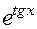 равен
равен  будет равен
будет равен  , где
, где 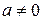 .
.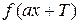 =
=  .
. будет основным периодом функции
будет основным периодом функции 
 будет число
будет число  , а основной период функций
, а основной период функций  буде равен
буде равен  .
. , или на любом другом промежутке длины
, или на любом другом промежутке длины 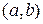 , если для любых
, если для любых 
 , выполняется неравенство
, выполняется неравенство 
 (
( ).
).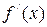 > 0 (
> 0 ( ) для всех значений
) для всех значений 
 . Например, функция
. Например, функция  имеет производную
имеет производную 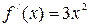 > 0 для всех
> 0 для всех  , а
, а  . Следовательно, эта функ-
. Следовательно, эта функ-

 , тогда
, тогда  непрерывна для любых
непрерывна для любых .
. . Но так как производная рассматриваемой функции не существует в точках
. Но так как производная рассматриваемой функции не существует в точках  ,
, 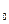 , x
, x 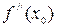 > 0, то точка
> 0, то точка  = 0,
= 0,  = 1. Для проверки этих точек на экстремум применим первый достаточный признак экстремума (второй признак не применим к точкам ± 1, так как в этих точках не существует производная
= 1. Для проверки этих точек на экстремум применим первый достаточный признак экстремума (второй признак не применим к точкам ± 1, так как в этих точках не существует производная  ). Из выражения для производной видно, что знаменатель дроби
). Из выражения для производной видно, что знаменатель дроби  для всех значений
для всех значений  , кроме
, кроме  (–1,0) производная отрицательна (функция монотонно убывает), а на промежутках (0,1)
(–1,0) производная отрицательна (функция монотонно убывает), а на промежутках (0,1)  =
=  –
–  , а
, а  =
=  > 0.
> 0.
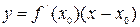 , то из определения следует, что кривая выпукла вверх на интервале
, то из определения следует, что кривая выпукла вверх на интервале  выполняется неравенство
выполняется неравенство  , и выпукла вниз на этом интервале, если
, и выпукла вниз на этом интервале, если ,
, 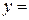
 является точкой перегиба кривой. 2). Если
является точкой перегиба кривой. 2). Если  . Находим,
. Находим, 
 =
=  , а
, а 
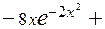


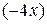 =
=  =
= 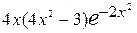 .
. ,
,  < 0 при
< 0 при  называется вертикальной асимптотой кривой
называется вертикальной асимптотой кривой  ,
, 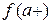 равен ∞.
равен ∞. 0 является вертикальной асимптотой кривой
0 является вертикальной асимптотой кривой  , так как правосторонний предел
, так как правосторонний предел  имеет две вертикальные асимптоты
имеет две вертикальные асимптоты  . Для более точного представления о поведении кривой при её приближении к асимптотам вычислим односторонние пределы. Имеем, предел слева
. Для более точного представления о поведении кривой при её приближении к асимптотам вычислим односторонние пределы. Имеем, предел слева  =
=  , предел справа
, предел справа  =
=  ; для вертикальной асимптоты
; для вертикальной асимптоты  =
=  , а правосторонний предел
, а правосторонний предел  =
=  .
.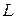 , заданная уравнением
, заданная уравнением  , называется наклонной асимптотой кривой
, называется наклонной асимптотой кривой  при
при  (при
(при  ), если расстояние от точки
), если расстояние от точки  этой кривой до прямой
этой кривой до прямой  ) при
) при  , то есть асимптота имеет уравнение
, то есть асимптота имеет уравнение  , её принято называть горизонтальной асимптотой. Отыскание наклонных асимптот основано на следующей теореме.
, её принято называть горизонтальной асимптотой. Отыскание наклонных асимптот основано на следующей теореме. а) существует
а) существует  (существует
(существует 
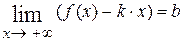 (существует
(существует 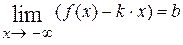 ).
). . Сначала ищется угловой коэффициент прямой
. Сначала ищется угловой коэффициент прямой  =
=  = =
= =  =
=  = 1. После того, как найден коэффициент k = =1, находим коэффициент
= 1. После того, как найден коэффициент k = =1, находим коэффициент  =
=  = =
= =  =
=  = 0. Вычисление коэффициентов
= 0. Вычисление коэффициентов  асимптоты проведено при
асимптоты проведено при  , так как вычисляемые пределы одинаковы как при
, так как вычисляемые пределы одинаковы как при  .
. ,
, 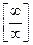 , [o∙∞],
, [o∙∞],  ,
, 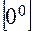 ,
,  , [∞ ─ ∞]. Неопределённости первых двух типов возникают при вычислении пределов вида
, [∞ ─ ∞]. Неопределённости первых двух типов возникают при вычислении пределов вида 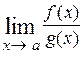 , когда числитель и знаменатель дроби одновременно стремятся к 0 или ∞, то есть
, когда числитель и знаменатель дроби одновременно стремятся к 0 или ∞, то есть 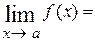
 либо
либо  = =
= =  (возможно
(возможно  = ∞). Такого рода неопределённости непосредственно раскрывает следующая теорема.
= ∞). Такого рода неопределённости непосредственно раскрывает следующая теорема. дифференцируемы на интервале
дифференцируемы на интервале  ≠ 0 на
≠ 0 на 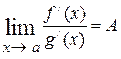 .
. .
. ,
,  . Утверждение этой теоремы остаётся верным и в случае правостороннего предела
. Утверждение этой теоремы остаётся верным и в случае правостороннего предела  ,
,  . Возможно также, что
. Возможно также, что 

 .
. . Видно, что
. Видно, что 
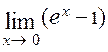 = 0.
= 0. =
=  = – 1.
= – 1. . Применив правило Лопиталя (числитель и знаменатель дроби стремятся к +∞ при
. Применив правило Лопиталя (числитель и знаменатель дроби стремятся к +∞ при 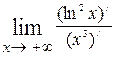 =
= 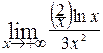 =
=  =
=  = 0.
= 0. , когда
, когда 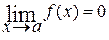 ,
,  . В этом случае исходный предел преобразуют к одному из двух видов
. В этом случае исходный предел преобразуют к одному из двух видов  либо
либо 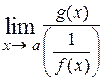 . В первом случае
. В первом случае  и
и  при x → a (неопределённость типа
при x → a (неопределённость типа  и
и  при
при  =
=  либо
либо  =
= 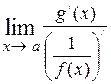 .
. . Так как
. Так как  , а
, а  , то имеем неопределённость типа [o∙∞]. Здесь удобнее отпра
, то имеем неопределённость типа [o∙∞]. Здесь удобнее отпра 


