
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремум функции двух переменныхСодержание книги Поиск на нашем сайте
Определение. Точка ∆ > 0 такое, что для любых точек плоскости Необходимый признак экстремума. Если точка Точки плоскости, в которых частные производные первого порядка равны нулю, называют стационарными точками функции Например, стационарные точки функции Из первого уравнения системы получаем Достаточный признак экстремума. Пусть точка
Пример. Найдём точки локального экстремума функции Таким образом, A = – 2 < 0, ∆ = 3 > > 0 и точка Пусть поверхность в пространстве задана уравнением
В частности, когда уравнение поверхности задано уравнением z = =
Составим уравнение касательной плоскости к поверхности, заданной уравнением
Задание 6. Определение. Функция Свойства первообразной. 1). Если
Неопределённый интеграл. Из свойств первообразной следует, что множество всех первообразных для функции
Определение. Неопределённым интегралом от функции вается множество всех первообразных для этой функции; неопределённый интеграл обозначают
Свойства неопределённого интеграла. 1). Линейность
Таблица неопределённых интегралов 1.
2.
3.
4.
5. 6.
7.
8.
9.
10.
Докажем равенство 10. По определению первообразной нужно доказать, что производная правой части этого равенства равна подинтегральной функции. Действительно, имеем
Пример. Вычислим + Формула интегрирования по частям. Если
которое называют формулой интегрирования по частям. Рассмотрим интегралы, которые вычисляются только с помощью этой формулы. 1. Интегралы вида Пример. Вычислим +
2. Интегралы вида
Пример. Вычислим с помощью формулы интегрирования по частям – частям) = +
3. Интегралы, в которых под знаком интеграла находятся обратные тригонометрические функции, тоже вычисляются интегрированием по частям. Это интегралы вида Пример. Вычислим
Замена переменной в неопределённом интеграле. Пусть функция Пример. Для вычисления + Пример. Для вычисления
Задание 7. Пусть функция Определение. Определённым интегралом от функции
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.231.160 (0.008 с.) |

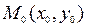 называется точкой локального максимума (локального минимума) функции
называется точкой локального максимума (локального минимума) функции  , если существует число
, если существует число , удовлетворяющих неравенству
, удовлетворяющих неравенству 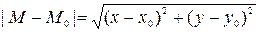 < ∆, выполняется неравенство
< ∆, выполняется неравенство 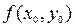 (
(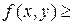
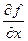 ,
,  , тогда
, тогда 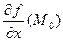 =
=  = 0.
= 0.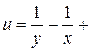
 являются решением системы двух уравнений с двумя неизвестными
являются решением системы двух уравнений с двумя неизвестными 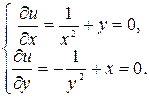
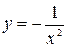 . Подставив это выражение во второе уравнение вместо y, получим равенство
. Подставив это выражение во второе уравнение вместо y, получим равенство  , из которого находим два корня
, из которого находим два корня 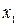 = 0,
= 0, 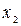 = 1. Первый корень не входит в область определения функции, а по второму корню
= 1. Первый корень не входит в область определения функции, а по второму корню 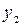 = –1 и стационарную точку
= –1 и стационарную точку  .
.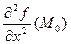 , B =
, B = 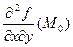 , C =
, C = 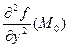 , ∆ = AC ─ B
, ∆ = AC ─ B 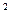 . Тогда: 1) если A > 0 и ∆ > 0, то
. Тогда: 1) если A > 0 и ∆ > 0, то  =
=  ,
, 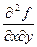 = 1,
= 1, 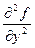 =
= 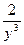 . Следовательно, A = =
. Следовательно, A = = 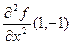 = ─2, B = 1, C =
= ─2, B = 1, C = 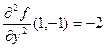 , ∆ = AC – B
, ∆ = AC – B 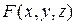 = 0 и точка
= 0 и точка 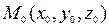 принадлежит этой поверхности, то есть
принадлежит этой поверхности, то есть 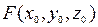 = =0. Тогда уравнение касательной плоскости, проведенной к этой поверхности в точке
= =0. Тогда уравнение касательной плоскости, проведенной к этой поверхности в точке 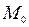 , имеет вид
, имеет вид +
+ 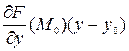 +
+ 
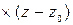 = 0.
= 0.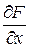 =
= 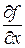 ,
,  =
=  ,
,  = –1, а уравнение касательной плоскости примет следующий вид
= –1, а уравнение касательной плоскости примет следующий вид +
+ 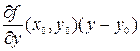 –
– 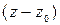 = 0, где
= 0, где  =
= 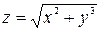 в точке (–1,2). Находим, что
в точке (–1,2). Находим, что 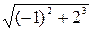 = 3. В нашем случае
= 3. В нашем случае  , следовательно,
, следовательно,  ,
,  . Таким образом,
. Таким образом,  ,
,  и уравнение искомой касательной плоскости имеет вид
и уравнение искомой касательной плоскости имеет вид 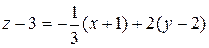 . Умножив последнее равенство на 3, и перенося всё в левую часть, получим окончательно
. Умножив последнее равенство на 3, и перенося всё в левую часть, получим окончательно  .
. называется первообразной для функции
называется первообразной для функции  на промежутке
на промежутке 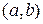 , если для любых
, если для любых 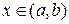 выполняется равенство
выполняется равенство 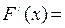
 , где
, где  – произвольная постоянная, тоже является первообразной для
– произвольная постоянная, тоже является первообразной для 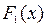 ,
,  – первообразные для функции
– первообразные для функции 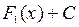 , где
, где  – первообразная для функции
– первообразная для функции 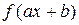 . Например,
. Например, 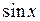 – первообразная для функции
– первообразная для функции 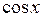 (так как
(так как  =
=  будет первообразной для функции
будет первообразной для функции 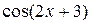 .
.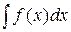 . Следовательно,
. Следовательно, 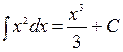 .
.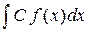 = =
= = 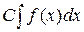 (постоянный множитель можно вынести за знак интеграла);
(постоянный множитель можно вынести за знак интеграла); 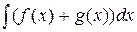 =
= 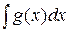 (интеграл от суммы функций равен сумме интегралов). Например,
(интеграл от суммы функций равен сумме интегралов). Например, 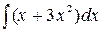 =
= 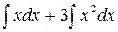 2) =
2) = 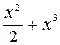 + +C. 2)
+ +C. 2)  =
= 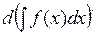 =
= 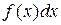 (дифференциал от неопределённого интеграла равен подинтегральному выражению).
(дифференциал от неопределённого интеграла равен подинтегральному выражению).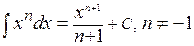 ;
;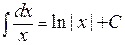 ;
;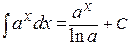 , в частности
, в частности 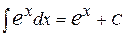 ;
; ;
;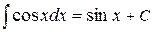 ;
;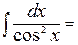
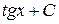 ;
;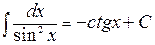 ;
; , в частности
, в частности 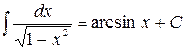 ;
;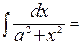
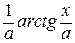
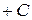 , в частности
, в частности 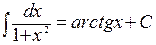 ;
;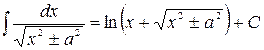 .
.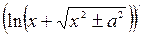 =
= 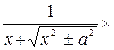
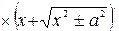 =
= 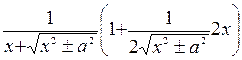 =
= 
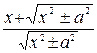 = =
= = 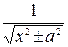 .
. . Поделив числитель подинтегральной дроби на знаменатель, а затем, применив свойство линейности неопределённого интеграла, получаем равенства
. Поделив числитель подинтегральной дроби на знаменатель, а затем, применив свойство линейности неопределённого интеграла, получаем равенства 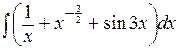 =
= 
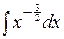 +
+ 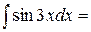
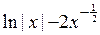 –
– 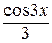
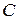 =
= 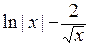 –
– 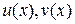 – непрерывно дифференцируемые функции, тогда справедливо равенство
– непрерывно дифференцируемые функции, тогда справедливо равенство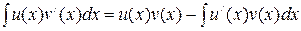 , (11)
, (11)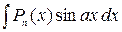 ,
,  ,
, 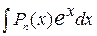 , где
, где  – полином степени
– полином степени 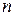 , вычисляются
, вычисляются  ,
,  , либо
, либо 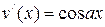 , либо
, либо  . При каждом интегрировании по частям степень полинома уменьшается на единицу.
. При каждом интегрировании по частям степень полинома уменьшается на единицу. . Воспользовавшись формулой (10), получим
. Воспользовавшись формулой (10), получим  = =
= =  –
– 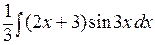 = (применим ещё раз формулу (11)) =
= (применим ещё раз формулу (11)) =  =
= 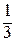
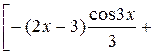
 =
=  .
. вычисляются
вычисляются 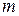 – кратным интегрированием по частям (формула интегрирования по частям применяется столько раз, какова степень логарифма). При этом полагают
– кратным интегрированием по частям (формула интегрирования по частям применяется столько раз, какова степень логарифма). При этом полагают  ,
, 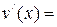
 . При каждом интегрировании по частям степень логарифма уменьшается на единицу.
. При каждом интегрировании по частям степень логарифма уменьшается на единицу.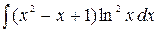 =
= 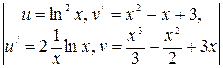 =
= 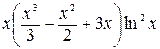 –
–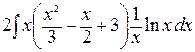 = (применим опять формулу интегрирования по
= (применим опять формулу интегрирования по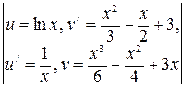 =
= 
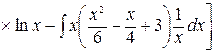 =
= 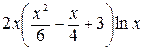 +
+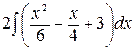 =
=  +
+  .
.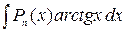 ,
,  ,
, 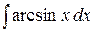 ,
,  . При вычислении этих интегралов за
. При вычислении этих интегралов за  обозначают обратные тригонометрические функции.
обозначают обратные тригонометрические функции.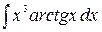 =
=  =
= 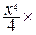
 –
–  =
= 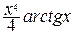 –
– 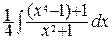 =
=  = =
= =  =
= 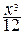 +
+ 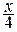 –
–  .
.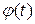 непрерывно дифференцируема, а функция
непрерывно дифференцируема, а функция 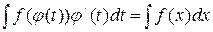 , которое называют формулой замены переменной в неопределённом интеграле.
, которое называют формулой замены переменной в неопределённом интеграле.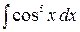 сделаем замену
сделаем замену 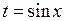 ,
, 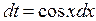 , тогда получим
, тогда получим  =
= 
 =
=  =
= 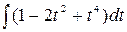 =
=  =
= 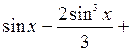
 .
.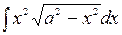 сделаем замену
сделаем замену  ,
, 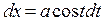 ,
,  , тогда получим
, тогда получим 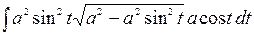 =
= 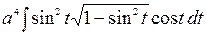 =
= 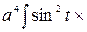
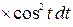 =
= 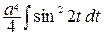 =
=  =
=  =
=  –
– 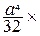
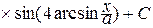 .
.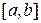 . Точки
. Точки 
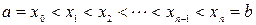 называют разбиением промежутка
называют разбиением промежутка 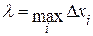 ,
, 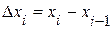 ,
, 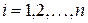 , называют рангом разбиения
, называют рангом разбиения 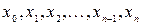 . Выберем произвольным образом
. Выберем произвольным образом 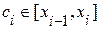 . Сумму
. Сумму 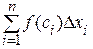 называют интегральной суммой для функции
называют интегральной суммой для функции 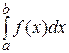 . Следовательно,
. Следовательно,  . Если определённый интеграл существует, то говорят, что функция
. Если определённый интеграл существует, то говорят, что функция 


