
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Матрицы. Определители.Содержание книги
Поиск на нашем сайте
Составитель Гайворонская С. А. Линейная алгебра Курс лекций
Воронеж
УДК 004.4 ББК 32.973
Утверждено научно-методическим советом факультета международных отношений ВГУ от 19.09.2012г., протокол №7.
Гайворонская С. А. Линейная алгебра: курс лекций для студентов факультета международных отношений / С. А. Гайворонская. – Воронеж: ФМО ВГУ, 2012. – 91 с.
Пособие подготовлено на кафедре международной экономики и внешнеэкономической деятельности факультета международных отношений Воронежского государственного университета. Учебное пособие предназначено для студентов, обучающихся на факультете международных отношений по направлению «Экономика», «Международные отношения», «Регионоведение». В пособии излагаются все изучаемые темы, предусмотренные программой. Приводится теоретический материал, большое количество примеров решения задач по рассмотренным темам. Тема 1. Матрицы. Определители. Матрицы. Определение. Прямоугольная таблица чисел вида
где Произведение Матрицы обозначаются прописными латинскими буквами А, В. Часто матрицу записывают в сокращенном виде
С помощью матриц удобно записывать некоторые экономические зависимости, например, таблицу распределения ресурсов, усл.ед., по отдельным отраслям экономики
может быть записана в компактной форме в виде матрицы
В этой записи матричный элемент Виды матриц Матрица, состоящая из одной строки, называется матрицей-строкой или вектором-строкой: Матрица, состоящая из одного столбца, называется матрицей-столбцом или вектором-столбцом: Если число строк матрицы n -го порядка равно числу ее столбцов, т.е. Например:
Упорядоченная совокупность элементов
Квадратная матрица называется диагональной, если ненулевыми могут быть только элементы главной диагонали, т.е. матрица имеет вид:
Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны единице:
Матрица, все элементы которой равны нулю, называется нулевой матрицей.
Две матрицы
Симметрические матрицы - это квадратные матрицы, у которых элементы симметричные относительно главной диагонали равны, т.е. Например: Операции над матрицами. Умножение матрицы на число Произведением матрицы А на действительное число Пример.
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы, например:
Сложение матриц Суммой двух матриц Пример.
Свойства операций суммирования матриц и произведения матрицы на число, непосредственно вытекающие из определений этих операций. Пусть 1. 2. 3. 4. 5. 6. 7. Умножение матриц Произведением матрицы При этом число Пример. Найти те произведения матриц Решение. Рассмотрим произведение матриц
число столбцов матрицы
Рассмотрим произведение матриц
Произведение матриц
Пример. Найти те произведения матриц
Решение. Рассмотрим произведение матриц
число столбцов матрицы
Рассмотрим произведение матриц
Произведение матриц
Возведение в степень. Целой положительной степенью
Операция возведения в степень определяется только для квадратных матриц. Пример. Найти Решение.
Транспонирование матриц Данная операция состоит в замене строк матрицы на ее столбцы с сохранением их порядка, или, что тоже самое, замене столбцов матрицы на ее строки. Пусть Пример. Вычислить определитель третьего порядка Решение.
Пусть дана квадратная матрица А n -го порядка. Минором Рассмотрим квадратную матрицу третьего порядка (1). Минором элемента
Минором элемента
Алгебраическим дополнением Пример. Найти алгебраические дополнения всех элементов матрицы
Решение.
Важное значение для вычисления определителей имеет следующая теорема. Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения:
Доказательство. Убедимся в справедливости теоремы на примере определителя третьего порядка. Разложим его по элементам первой строки:
Свойства определителей
1. Если все элементы некоторого столбца или некоторой строки определителя равны нулю, то и сам определитель равен нулю. 2. Умножение всех элементов одного столбца или одной строки определителя на любое число Замечание. За знак определителя можно выносить общий множитель любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех элементов. Пример.
3. Величина определителя не изменится, если его строки и столбцы поменять местами. 4. При транспонировании матрицы ее определитель не изменяется: 5. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный. 6. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен нулю. 7. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю. 8. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю, т.е.
9. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число. 10. Определитель произведения двух квадратных матриц равен произведению их определителей: Замечание. Из свойства 10 следует, что даже если 11. Определитель треугольной матрицы равен произведению ее диагональных элементов. Перечисленные свойства определителей позволяют существенно упростить их вычисления, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1-10, чтобы преобразованная матрица имела строку (столбец), содержащую как можно больше нулей, а затем найти определитель разложением по этой строке (столбцу).
Пример. Вычислить определитель четвертого порядка
Решение. Преобразуем определитель так, чтобы в третьей строке все элементы, кроме одного обращались в нуль. Для этого умножим, например, элементы третьего столбца на (-4) и прибавим их к первому столбцу:
Далее умножим элементы третьего столбца на 2 и прибавим их ко второму столбцу, далее применим к полученному определителю четвертого порядка теорему Лапласа:
Полученный определитель третьего порядка можно вычислить по правилу треугольника или используя теорему Лапласа, но можно продолжить упрощение матрицы. «Обнулим» в матрице третьего порядка элементы второй строки (кроме одного). Для этого умножим элементы третьего столбца на (-13) и на 4 и прибавим соответственно к первому и второму столбцам:
при вычислении определителя второго порядка используем свойство определителя: за знак определителя можно выносить общий множитель любой строки или столбца (вынесем из первого столбца число 8, а из второго столбца число 18):
Обратная матрица Понятие обратной матрицы распространяется только на квадратные матрицы. Определение. Матрица
Теорема. Для того чтобы матрица
Пусть дана невырожденная матрица
тогда обратной к матрице
где Ранг матрицы Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы. Пусть дана матрица
В матрице А вычеркиванием каких-либо строк или столбцов можно вычленить квадратные подматрицы k -го порядка, где Определение. Рангом матрицы Ранг матрицы обозначается 1. Ранг матрицы 2. 3. Для квадратной матрицы Пример. Вычислить ранг матрицы
Решение. Матрица
Пример. Вычислить ранг матрицы.
Решение. Для матрицы
Поскольку все миноры третьего порядка равны нулю, то ранг матрицы Так как существует ненулевой минор второго порядка, например,
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы. Назовем элементарными преобразованиями матрицы следующие: - отбрасывание нулевой строки (столбца); - умножение всех элементов строки (столбца) матрицы на число не равное нулю; - изменение порядка строк (столбцов) матрицы; - прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число; - транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при ее элементарных преобразованиях.
Две матрицы называются эквивалентными, если одна получается из другой с помощью конечного числа элементарных преобразований. Эквивалентные матрицы имеют одинаковые ранги. С помощью эквивалентных преобразований можно привести матрицу к так называемому ступенчатому виду. Матрица
где Замечание. Условие Очевидно, что ранг ступенчатой матрицы равен
Пример. Найти ранг матрицы
Решение. 1. Если
2. Если
3. Если в полученной матрице
Если в процессе преобразования получаются строки (столбцы), целиком состоящие из нулей, то эти строки (столбцы) отбрасываем. Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка не равные нулю, например,
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов. Пусть дана матрица
В матрице
Две строки матрицы называются равными, если равны их соответствующие элементы: Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка
где
Строки матрицы
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных. Если линейная комбинация строк (2) равна нулю тогда и только тогда, когда все коэффициенты Теорема. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы. Строки и столбцы матрицы, участвующие в образовании базисного минора, также называются базисными.
Теорема. Всякая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).
Пример. Решить систему уравнений методом Крамера:
Решение.
Существенным недостатком решения систем Метод Гаусса Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Предположим, что в системе (3)
коэффициент Шаг 1. Умножая первое уравнение на подходящие числа
где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после шага 1.
Шаг 2. Предположим, что Умножая второе уравнение на подходящие числа Продолжая процесс последовательного исключения переменных
Число нуль в последних
Если хотя бы одно из чисел Таким образом, для любой совместной системы числа - число уравнений системы (9) равно числу переменных, т.е. - Пер
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.015 с.) |

 называется матрицей,
называется матрицей, - действительные числа, называемые элементами матрицы,
- действительные числа, называемые элементами матрицы,  ;
; 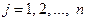 ,
,  и
и  - соответственно индексы строки и столбца.
- соответственно индексы строки и столбца. числа строк на число столбцов называют размером матрицы.
числа строк на число столбцов называют размером матрицы.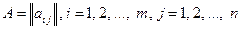 .
.
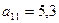 показывает, сколько электроэнергии потребляет промышленность, а элемент
показывает, сколько электроэнергии потребляет промышленность, а элемент 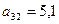 - сколько водных ресурсов требуется для сельского хозяйства.
- сколько водных ресурсов требуется для сельского хозяйства. .
. .
. , то матрица называется квадратной n -го порядка.
, то матрица называется квадратной n -го порядка. - квадратная матрица, размером
- квадратная матрица, размером  .
. называется главной диагональю квадратной матрицы:
называется главной диагональю квадратной матрицы:

 .
. - единичная матрица третьего порядка.
- единичная матрица третьего порядка. и
и  называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны.
называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны. ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. называется матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число
называется матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число  ;
; 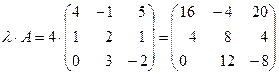

 и
и  одинакового размера называется матрица
одинакового размера называется матрица  каждый элемент которой равен сумме соответствующих элементов матриц
каждый элемент которой равен сумме соответствующих элементов матриц 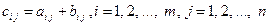 , т.е. матрицы складываются поэлементно.
, т.е. матрицы складываются поэлементно.
 ,
,  и
и  – матрицы, имеющие одинаковый размер, а
– матрицы, имеющие одинаковый размер, а  и
и  – некоторые действительные числа, тогда:
– некоторые действительные числа, тогда: .
. .
. .
. .
. .
. , где
, где  - нулевая матрица.
- нулевая матрица. .
. размера
размера  на матрицу
на матрицу  размера
размера  называется матрица
называется матрица 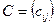 размера
размера  , у которой элемент
, у которой элемент  равен сумме произведений элементов
равен сумме произведений элементов  -й строки матрицы
-й строки матрицы  -ого столбца матрицы
-ого столбца матрицы  ,
,  ,
,  .
. столбцов матрицы
столбцов матрицы  , т.е. размер матрицы
, т.е. размер матрицы  .
. ,
, 


 определено:
определено: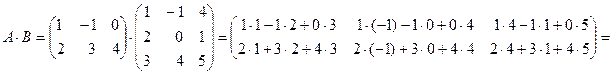



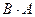 не имеет смысла, так как число столбцов матрицы
не имеет смысла, так как число столбцов матрицы 


 .
.

 квадратной матрицы
квадратной матрицы 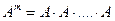
 , где
, где  .
. .
. , тогда транспонированная матрица имеет вид:
, тогда транспонированная матрица имеет вид:  , например
, например  ,
, 
 .
. .
. элемента
элемента  матрицы n -го порядка называется определитель матрицы
матрицы n -го порядка называется определитель матрицы  -го порядка, полученный из матрицы А вычеркиванием i- строки и j- столбца, на пересечении которых расположен этот элемент.
-го порядка, полученный из матрицы А вычеркиванием i- строки и j- столбца, на пересечении которых расположен этот элемент. матрицы третьего порядка является определитель второго порядка:
матрицы третьего порядка является определитель второго порядка:

 матрицы третьего порядка является определитель второго порядка:
матрицы третьего порядка является определитель второго порядка:

 элемента
элемента  , где
, где 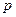 - сумма номеров строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение элемента обозначается такой же прописной буквой, что и сам элемент. Так алгебраическое дополнение элемента
- сумма номеров строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение элемента обозначается такой же прописной буквой, что и сам элемент. Так алгебраическое дополнение элемента  , алгебраическое дополнение элемента
, алгебраическое дополнение элемента 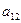 обозначается
обозначается  .
.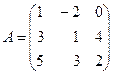
 ;
;  ;
; ;
;  ;
; ;
; 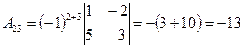 ;
; ;
;  ;
; .
. - разложение по элементам i -ой строки, i=1, 2,…,n.
- разложение по элементам i -ой строки, i=1, 2,…,n. - разложение по элементам j -ого столбца, j=1, 2,…,n.
- разложение по элементам j -ого столбца, j=1, 2,…,n.


 - полученное выражение совпадает с определением определителя третьего порядка. Аналогичный результат получаем при разложении определителя матрицы по любой строке или столбцу.
- полученное выражение совпадает с определением определителя третьего порядка. Аналогичный результат получаем при разложении определителя матрицы по любой строке или столбцу. , но
, но
 .
. при
при  .
. ,
,  - матрицы
- матрицы  -го порядка, тогда
-го порядка, тогда  .
. , то
, то  .
.










 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице  .
.
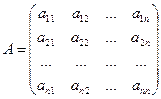 ,
,
 - алгебраические дополнения соответственно элементов
- алгебраические дополнения соответственно элементов  .
.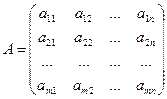
 . Определители таких подматриц называются минорами
. Определители таких подматриц называются минорами  можно получить подматрицы первого, второго и третьего порядков.
можно получить подматрицы первого, второго и третьего порядков. или
или  . Из определения следует:
. Из определения следует: не превосходит меньшего из ее размеров, т.е.
не превосходит меньшего из ее размеров, т.е.  .
.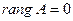 тогда и только тогда, когда все элементы матрицы
тогда и только тогда, когда все элементы матрицы  тогда и только тогда, когда матрица
тогда и только тогда, когда матрица 
 . Однако
. Однако  , т.к. матрица
, т.к. матрица  . Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют определители равные нулю, т.е.
. Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют определители равные нулю, т.е. 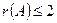 . Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо пропорциональные столбцы (первый и третий), поэтому тоже имеют определители равные нулю. Таким образом,
. Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо пропорциональные столбцы (первый и третий), поэтому тоже имеют определители равные нулю. Таким образом,  . Поскольку матрица
. Поскольку матрица  .
.
 . Проверим, равен ли ранг трем. Для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего четыре, они получаются при вычеркивании одного из столбцов матрицы):
. Проверим, равен ли ранг трем. Для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего четыре, они получаются при вычеркивании одного из столбцов матрицы): ;
;  ;
;  ;
; .
. , то ранг
, то ранг 

 .
.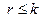 всегда может быть достигнуто транспонированием матрицы.
всегда может быть достигнуто транспонированием матрицы. , так как имеется минор
, так как имеется минор 
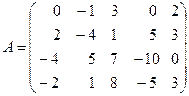
 , то перестановкой строк или столбцов добиваемся того, чтобы
, то перестановкой строк или столбцов добиваемся того, чтобы  . В данном примере поменяем местами первую и вторую строки матрицы.
. В данном примере поменяем местами первую и вторую строки матрицы.
 и прибавим к третьей строке, затем умножим первую строку на
и прибавим к третьей строке, затем умножим первую строку на  и прибавим к четвертой строке (во второй строке элемент
и прибавим к четвертой строке (во второй строке элемент  , поэтому вторая строка не меняется):
, поэтому вторая строка не меняется):

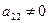 , то умножая элементы второй строки на подходящие числа и прибавляя к третьей и четвертой строкам, добьемся того, чтобы все элементы второго столбца (кроме
, то умножая элементы второй строки на подходящие числа и прибавляя к третьей и четвертой строкам, добьемся того, чтобы все элементы второго столбца (кроме  ) равнялись нулю. В нашем примере умножим вторую строку на
) равнялись нулю. В нашем примере умножим вторую строку на  и прибавим к третьей строке, затем умножим вторую строку на
и прибавим к третьей строке, затем умножим вторую строку на  и прибавим к четвертой строке:
и прибавим к четвертой строке:

 , поэтому ранг полученной ступенчатой, а следовательно и исходной матрицы равен двум
, поэтому ранг полученной ступенчатой, а следовательно и исходной матрицы равен двум  .
. .
.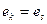 , если
, если  .
. ;
;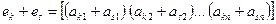 .
. называется линейной комбинацией строк
называется линейной комбинацией строк  матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:
матрицы, если она равна сумме произведений этих строк на произвольные действительные числа: ,
, - любые числа.
- любые числа. называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа  , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке
, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке (2)
(2) , равны нулю, т.е.
, равны нулю, т.е.  , то строки
, то строки  называются линейно независимыми.
называются линейно независимыми. .
. , данная система имеет единственное решение.
, данная система имеет единственное решение.


 ,
,  ,
,  .
.
 не равен нулю (если это не так, то перестановкой уравнений местами добьемся того, чтобы
не равен нулю (если это не так, то перестановкой уравнений местами добьемся того, чтобы  и прибавляя полученные уравнения соответственно ко второму, третьему,…,
и прибавляя полученные уравнения соответственно ко второму, третьему,…,  -му уравнению системы, исключаем переменную
-му уравнению системы, исключаем переменную 
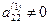 (если это не так, то перестановкой уравнений местами добьемся того, чтобы
(если это не так, то перестановкой уравнений местами добьемся того, чтобы  и прибавляя полученные уравнения соответственно к третьему, четвертому, …,
и прибавляя полученные уравнения соответственно к третьему, четвертому, …,  из всех последующих уравнений, начиная с третьего.
из всех последующих уравнений, начиная с третьего.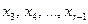 , после
, после  -го шага получаем систему
-го шага получаем систему (9)
(9)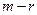 уравнениях означает, что их левые части имеют вид:
уравнениях означает, что их левые части имеют вид:
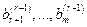 не равно нулю, то соответствующее равенство противоречиво и система (1) несовместна.
не равно нулю, то соответствующее равенство противоречиво и система (1) несовместна. (в этом случае система (9) имеет треугольный вид;
(в этом случае система (9) имеет треугольный вид; , в этом случае система (9) имеет ступенчатый вид.
, в этом случае система (9) имеет ступенчатый вид.


