
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства арифметических операций над комплексными числамиСодержание книги
Поиск на нашем сайте 1.
2. Модуль произведения (частного) двух комплексных чисел равен произведению (частному) модулей этих чисел, а его аргумент – сумме (разности) аргументов этих чисел, т.е.,
если
если
Геометрически умножение числа Так как в соответствии с формулами (93) и (94) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, то формула Муавра - возведения комплексного числа в натуральную степень
Пример. Комплексные числа Решение. 1. Запишем тригонометрическую форму комплексного числа 2. Выполним аналогичные действия для комплексного числа 3. Применяя формулы (93) и (94), получаем:
Пример. Найти Решение. В примере, решенном ранее, была получена тригонометрическая форма для комплексного числа
Рассмотрим извлечение корня из комплексного числа. Пусть
Тогда, используя определение корня и формулу Муавра, получаем
Откуда следует, что
Итак,
где При
Пример. Найти Решение. В примере, решенном ранее, была получена тригонометрическая форма для комплексного числа
откуда получаем три значения корня
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера:
тогда показательная форма комплексного числа имеет вид:
Пример. Комплексные числа Решение. Ранее было получено
Следовательно, по формуле (98) получим:
Оглавление
Литература
1. Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман: под ред. Н.Ш. Кремера. – 3-е изд.. – М.: Издательство Юрайт; ИД Юрайт, 2012. – 909 с. 2. Шипачев В.С. Высшая математика. Учебник.- М.: Высшая школа, 2003.-479 с. 3. Красс М.С. Математика для экономических специальностей. Учебник. - М.: ИНФРА-М, 1998. – 464 с. 4. Шипачев В.С. Задачник по высшей математике. Учебное пособие для вузов. - М.: Высшая школа, 2003.- 304 c. 5. Минорский В.П. Сборник задач по высшей математике: Учеб. Пособие для втузов.- 14-е изд., испр. - М.: Издательство Физико-математической литературы, 2001. – 336 с. 6. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике: учебник. - ч. 1. – М.: Финансы и статистика, 2000. – 224 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

 При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.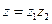 , то
, то  ,
,  и
и , (93)
, (93) , то
, то  ,
,  и
и (94)
(94) на число
на число  означает изменение длины радиуса-вектора
означает изменение длины радиуса-вектора  (или
(или  ) в
) в  (или
(или  ).
). , имеет вид:
, имеет вид: (95)
(95) и
и  представить в тригонометрической форме и найти
представить в тригонометрической форме и найти  и
и  .
. , т.к.
, т.к.  , то
, то  , т.к.
, т.к.  , то
, то  , тогда
, тогда  , т.е.
, т.е. 
 , т.к.
, т.к.  , т.к.
, т.к.  , тогда
, тогда  , т.е.
, т.е.  .
.


 .
. .
. . Поэтому по формуле Муавра находим:
. Поэтому по формуле Муавра находим:
 .
.
 или
или
 и
и 
 ,
,  , т.е.
, т.е. , (96)
, (96) .
. значения корня будут повторяться. Таким образом, корень
значения корня будут повторяться. Таким образом, корень  .
. .
.



 , расположенные на окружности радиуса
, расположенные на окружности радиуса  .
. (97)
(97) (98)
(98) ,
, 
 ,
,  .
. линейных уравнений с
линейных уравнений с 


