
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод обратной матрицы и метод Крамера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим частный случай системы (3), когда число уравнений равно числу неизвестных, т.е.
Составим квадратную матрицу А порядка
В матричной форме система уравнений (5) имеет вид:
где матрицы
Когда порядок матриц Другой метод решения системы уравнений (5) основан на теореме Крамера (Габриэль Крамер (1704-1752) швейцарский математик)). Рассмотрим решение системы двух уравнений с двумя переменными
в которой хотя бы один из коэффициентов при переменных отличен от нуля. Для решения этой системы исключим переменную
Выражение в скобках есть определитель системы
Обозначим
Из полученной системы следует, что если определитель системы Если определитель системы
Если определитель системы
Вернемся к системе линейных уравнений (5). Составим определитель матрицы А:
который называется определителем системы. Заменим в этом определителе
Теорема (правило Крамера). Пусть
Ранее мы фактически получили формулы Крамера в частном случае при решении системы (8) – системы двух уравнений с двумя переменными. Пример. Решить систему уравнений методом Крамера:
Решение.
Существенным недостатком решения систем Метод Гаусса Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Предположим, что в системе (3)
коэффициент Шаг 1. Умножая первое уравнение на подходящие числа
где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после шага 1.
Шаг 2. Предположим, что Умножая второе уравнение на подходящие числа Продолжая процесс последовательного исключения переменных
Число нуль в последних
Если хотя бы одно из чисел Таким образом, для любой совместной системы числа - число уравнений системы (9) равно числу переменных, т.е. - Переход системы (1) к равносильной системе (9) называется прямым ходом метода Гаусса, а нахождение переменных из системы (9) – о братным ходом. Преобразования Гаусса удобно проводить, осуществляя их не с самими уравнениями, а с матрицей их коэффициентов – расширенной матрицей:
Пример. Решить систему уравнений
Решение. Расширенная матрица системы имеет вид:
Так как
Умножаем третью строку на
В результате матрица системы приведена к треугольному виду. Используя последнюю матрицу, перейдем к системе уравнений:
Откуда, используя обратный ход метода Гаусса, найдем из четвертого уравнения Пример. Методом Гаусса решить систему уравнений.
Решение: Преобразуем расширенную матрицу системы
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво, так как в результате преобразований получено неверное равенство 0= -1, следовательно, данная система несовместна.
4.5. Система Ранее было установлено, что ранг матрицы равен максимальному числу ее линейно независимых строк, поэтому если строки расширенной матрицы, т.е. уравнения системы (3) линейно независимы, то ранг расширенной матрицы равен числу ее уравнений, т.е. Вопрос о разрешимости системы уравнений (3) в общем виде рассматривается в следующей теореме.
Теорема Кронекера-Капелли (Кронекер Леопольд (1823 – 1891) – немецкий математик, Капели Альфредо (1855 – 1910) – итальянский математик). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Для совместных систем линейных уравнений верны следующие теоремы. Теорема 1. Если ранг матрицы совместной системы равен числу переменных, т.е. Теорема 2. Если ранг матрицы совместной системы меньше числа переменных, т.е.
Пусть Решение системы (3), в котором все Так как каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний, то и базисных решений имеется не более
Таким образом, совместная система Метод Гаусса по сравнению с другими методами имеет следующие достоинства: - значительно менее трудоемкий; - позволяет однозначно установить совместна система или нет, а в случае совместности найти ее решения (единственное или бесконечное множество); - дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы. Пример 1. С помощью метода Гаусса решить систему
Решение. Преобразуем расширенную матрицу системы (для удобства вычислений берем в качестве первой строки коэффициенты второго уравнения, у которого коэффициент при
Один из миноров матрицы системы, например, Рассмотренный минор является базисным минором, составленным из коэффициентов при переменных
откуда
Задавая неосновным переменным произвольные значения
В качестве основных переменных можно было взять другие их группы с отличным от нуля базисным минором. Для каждой такой группы получится «свое» общее решение, но все общие решения равносильны в том смысле, что они определяют равные бесконечные множества частных решений, получаемых из общего при фиксированных значениях неосновных переменных. Пример 2. Найти все базисные решения системы, приведенной в примере 1. Решение. Ранг матрицы системы Общее число групп основных переменных не более чем Выясним, могут ли переменные Найдем базисное решение, взяв в качестве основных переменных
откуда Если взять за основные переменные Замечание. Все базисные переменные системы можно было найти из общего решения, полученного в примере 1, приравнивая соответствующие переменные нулю. Например, при
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 976; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.86.134 (0.008 с.) |

 . Система уравнений имеет вид:
. Система уравнений имеет вид: (5)
(5) этой системы:
этой системы: . (6)
. (6)
 и
и  имеют размер
имеют размер  . Пусть матрица системы
. Пусть матрица системы 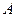 является невырожденной, т.е. существует обратная матрица
является невырожденной, т.е. существует обратная матрица  . Умножив обе части этого уравнения слева на
. Умножив обе части этого уравнения слева на  , используя свойства произведения матриц получаем
, используя свойства произведения матриц получаем  , откуда
, откуда  и решением системы методом обратной матрицы будет матрица-столбец
и решением системы методом обратной матрицы будет матрица-столбец (7)
(7) (8)
(8) , умножив первое уравнение системы на
, умножив первое уравнение системы на  , а второе – на
, а второе – на 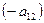 и сложив их. Затем исключим переменную
и сложив их. Затем исключим переменную  , умножив первое уравнение системы на
, умножив первое уравнение системы на  , а второе – на
, а второе – на  и также сложив их. В результате получим систему
и также сложив их. В результате получим систему (9)
(9)
 ;
;  , тогда система (7) примет вид
, тогда система (7) примет вид (10)
(10) , то система (8) имеет единственное решение, определяемое по формулам:
, то система (8) имеет единственное решение, определяемое по формулам:  .
.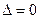 , а
, а  (или
(или  ), то система (8) несовместная, так как в этом случае она приводится к виду:
), то система (8) несовместная, так как в этом случае она приводится к виду:
 , то система (8) неопределенная, так как в этом случае она приводится к виду:
, то система (8) неопределенная, так как в этом случае она приводится к виду:
 ,
, -й столбец на столбец свободных членов
-й столбец на столбец свободных членов 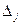 :
:

 - определитель матрицы системы
- определитель матрицы системы  ,
, 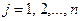 .
. .
. , данная система имеет единственное решение.
, данная система имеет единственное решение.


 ,
,  ,
,  .
.
 ).
). и прибавляя полученные уравнения соответственно ко второму, третьему,…,
и прибавляя полученные уравнения соответственно ко второму, третьему,…,  -му уравнению системы, исключаем переменную
-му уравнению системы, исключаем переменную 
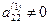 (если это не так, то перестановкой уравнений местами добьемся того, чтобы
(если это не так, то перестановкой уравнений местами добьемся того, чтобы  и прибавляя полученные уравнения соответственно к третьему, четвертому, …,
и прибавляя полученные уравнения соответственно к третьему, четвертому, …, 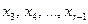 , после
, после  -го шага получаем систему
-го шага получаем систему (9)
(9)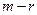 уравнениях означает, что их левые части имеют вид:
уравнениях означает, что их левые части имеют вид:
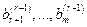 не равно нулю, то соответствующее равенство противоречиво и система (1) несовместна.
не равно нулю, то соответствующее равенство противоречиво и система (1) несовместна. (в этом случае система (9) имеет треугольный вид;
(в этом случае система (9) имеет треугольный вид; , в этом случае система (9) имеет ступенчатый вид.
, в этом случае система (9) имеет ступенчатый вид.



 , то умножая первую строку матрицы на числа
, то умножая первую строку матрицы на числа  и прибавляя полученные строки соответственно ко второй, третьей и четвертой строкам, исключаем переменную
и прибавляя полученные строки соответственно ко второй, третьей и четвертой строкам, исключаем переменную  из всех строк, начиная со второй. В полученной матрице
из всех строк, начиная со второй. В полученной матрице 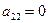 , поэтому меняем местами вторую и третью строки матрицы, добиваясь, чтобы элемент
, поэтому меняем местами вторую и третью строки матрицы, добиваясь, чтобы элемент  . Далее умножаем вторую строку на
. Далее умножаем вторую строку на  и прибавляем к третьей строке:
и прибавляем к третьей строке:

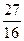 и прибавляем к четвертой строке:
и прибавляем к четвертой строке:


 ; из третьего уравнения
; из третьего уравнения  ; из второго уравнения
; из второго уравнения  и из первого уравнения
и из первого уравнения  , т. е. решение системы
, т. е. решение системы  .
.


 . Если уравнения линейно зависимы, то
. Если уравнения линейно зависимы, то  .
.
 ,
,  переменных
переменных  называют основными, или базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные
называют основными, или базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные 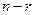 ёёпеременных называются неосновными, или свободными.
ёёпеременных называются неосновными, или свободными.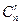
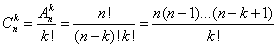
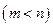 имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее
имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее  .
.

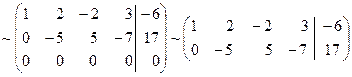 ,
, , следовательно, ранг матрицы системы равен порядку ненулевого минора и равен двум, т.е.
, следовательно, ранг матрицы системы равен порядку ненулевого минора и равен двум, т.е.  .
. , следовательно, за основные переменные берем
, следовательно, за основные переменные берем  переносим в правые части уравнений. В результате получаем систему:
переносим в правые части уравнений. В результате получаем систему:


 находим бесконечное множество решений системы, т.е. общее решение системы:
находим бесконечное множество решений системы, т.е. общее решение системы:
 , поэтому возможны следующие группы основных переменных
, поэтому возможны следующие группы основных переменных  ;
;  ;
; 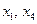 ;
;  ;
;  ;
; 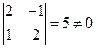 , то
, то 
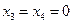 , получим систему уравнений в виде:
, получим систему уравнений в виде: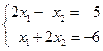
 , т.е. первое базисное решение будет
, т.е. первое базисное решение будет  .
. , то получим второе базисное решение
, то получим второе базисное решение  . Аналогично находятся и остальные базисные решения
. Аналогично находятся и остальные базисные решения 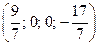 ,
, 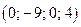 и
и  .
. получаем базисное решение
получаем базисное решение  или при
или при  получаем базисное решение
получаем базисное решение 


