
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные значения и собственные векторы матрицы.Содержание книги
Поиск на нашем сайте
Рассмотрим квадратные матрицы размера При умножении матрицы порядка
Для любой матрицы существует набор особых векторов, таких, что произведение матрицы на вектор из такого набора равносильно умножению этого вектора на определенное число.
Определение. Число
При этом Уравнение (44) представлено в матричной форме. Группируя все слагаемые этого уравнения в левой части, его можно переписать в более удобном виде:
где Если
Множество всех собственных значений матрицы
Собственные значения и собственные векторы линейного оператора Определение. Вектор
Число Из определения следует, что собственный вектор под действием линейного оператора Равенство (47) можно записать в матричной форме
где вектор
Перепишем систему так, чтобы в правых частях были нули:
или в матричном виде
Полученная однородная система всегда имеет нулевое решение
Определитель Характеристический многочлен линейного оператора не зависит от выбора базиса. Действительно, преобразуем характеристический многочлен
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц, получаем
Пример. Найти собственные значения и собственные векторы линейного оператора Решение. Составляем характеристическое уравнение
Откуда собственные значения линейного оператора
или
Откуда находим Аналогично можно убедиться, что векторы Свойства собственных значений матрицы линейного оператора 1. Произведение собственных значений матрицы
2. Число отличных от нуля собственных значений матрицы 3. Все собственные значения матрицы отличны от нуля тогда и только тогда, когда матрица 4. Если 5. Если l - собственное значение матрицы
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.127.152 (0.006 с.) |

 или, что то же самое, матрицы порядка
или, что то же самое, матрицы порядка  .
.
 называется собственным значением матрицы
называется собственным значением матрицы  порядка
порядка  , что выполняется равенство
, что выполняется равенство (44)
(44) называется собственным вектором матрицы
называется собственным вектором матрицы  (45)
(45) и
и  - соответственно единичная матрица и нулевой вектор.
- соответственно единичная матрица и нулевой вектор. - элементы матрицы
- элементы матрицы  согласно определениям умножения матрицы на число и суммы матриц имеет вид:
согласно определениям умножения матрицы на число и суммы матриц имеет вид: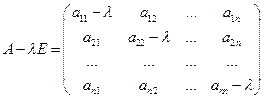 (46)
(46) .
. называется собственным вектором линейного оператора
называется собственным вектором линейного оператора 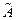 (или матрицы
(или матрицы  (47)
(47) (48)
(48) представлен в виде вектора-столбца, или в развернутом виде
представлен в виде вектора-столбца, или в развернутом виде
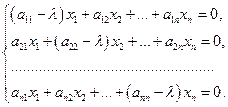

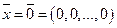 . Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы
. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы (49)
(49) является многочленом
является многочленом  , полученный в новом базисе
, полученный в новом базисе  , если известна матрица
, если известна матрица  перехода от старого базиса
перехода от старого базиса  к новому. С учетом соотношений
к новому. С учетом соотношений 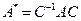 получаем
получаем .
. , т.е.
, т.е. независимо от выбора базиса.
независимо от выбора базиса.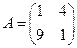 .
.

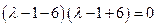
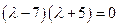
 ,
,  . Находим собственный вектор
. Находим собственный вектор  , соответствующий собственному значению
, соответствующий собственному значению 

 ,
,
 . Положив
. Положив 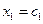 , получим, что векторы
, получим, что векторы 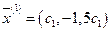 при любом
при любом  являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  при любом
при любом  являются собственными векторами линейного оператора
являются собственными векторами линейного оператора  .
. - собственное значение невырожденной матрицы
- собственное значение невырожденной матрицы  - собственное значение обратной матрицы
- собственное значение обратной матрицы 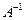 .
. - собственное значение матрицы
- собственное значение матрицы  , где
, где  - натуральное число.
- натуральное число.


