
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скаляры и векторы. Операции над векторамиСодержание книги
Поиск на нашем сайте Многие характеристики окружающих нас явлений описываются числами, например, вес товара и его стоимость, температура тела, количество мест в салоне самолета. Такие величины называются скалярными, или скалярами. Однако имеются и такие величины, которые требуют для своего описания еще и указания направления, например, скорость и ускорение при движении тела. Такие величины называются векторными, или векторами. Определение. Направленный отрезок, на котором заданы начало, конец и направление, называется вектором.
Определение. Векторы
Определение. Векторы
В любой системе координат вектор характеризуется своими координатами: двумя координатами на плоскости Если заданы координаты начала и конца вектора, соответственно
Длина вектора
Нулевым вектором называется вектор
Операции над векторами. Пусть даны два вектора 1. Суммой векторов
Для получения суммы векторов нужно совместить конец вектора
2. Геометрический смысл умножения вектора на число состоит в увеличении длины вектора в λ раз при
Из определения коллинеарности векторов и из определения произведения вектора на число вытекает, что векторы
Это соотношение носит название условия коллинеарности двух векторов. Скалярное произведение векторов Пусть Скалярным произведением двух векторов
Скалярное произведение векторов обладает следующими свойствами: 1. 2. 3. 4. 5. Скалярное произведение векторов выражается через их координаты следующим образом: пусть даны векторы
Тогда формула для определения угла между векторами имеет вид:
Векторное пространство Понятие и основные свойства векторов
Приведем обобщение соответствующих понятий на Определение. Любой упорядоченный набор из Определение. Совокупность всех Координаты Определение. Два вектора с одним и тем же числом координат Определение. Вектор, все координаты которого равны нулю, называется нулевым Операции над векторами Пусть векторы 1. Суммой векторов
2. Пусть Из введенных таким образом операций над векторами вытекают следующие свойства этих операций. Пусть 1. 2. 3. 4. 5. 6. 7. Для любого вектора 8.
Определенное 1. Для любых двух векторов 2. Для любого числа λ и вектора
Определение. Пусть U – подмножество линейного пространства Например, совокупность всех векторов
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.006 с.) |

 Обозначается вектор символом, куда входят его начало и конец
Обозначается вектор символом, куда входят его начало и конец  или одной буквой
или одной буквой  . Расстояние между началом и концом вектора называется его длиной.
. Расстояние между началом и концом вектора называется его длиной.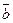 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

 и тремя - в пространстве
и тремя - в пространстве  .
.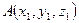 и
и  , то координаты этого вектора определяются по формуле:
, то координаты этого вектора определяются по формуле:
 .
. на плоскости и
на плоскости и  в пространстве.
в пространстве. и
и  .
.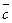 , координаты которого равны суммам соответствующих координат векторов
, координаты которого равны суммам соответствующих координат векторов 
 будет направлен от начала первого вектора к концу второго.
будет направлен от начала первого вектора к концу второго.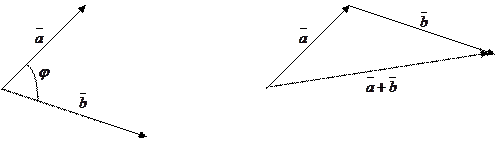
 Произведением вектора
Произведением вектора  на число
на число 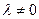 называется вектор
называется вектор  , координаты которого соответственно равны
, координаты которого соответственно равны  .
.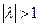 или ее сокращении в λ раз при
или ее сокращении в λ раз при  . При
. При  вектор
вектор 

 - перестановочность сомножителей.
- перестановочность сомножителей.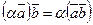 - сочетательность относительно умножения на число.
- сочетательность относительно умножения на число. - распределительность относительно суммы векторов.
- распределительность относительно суммы векторов.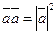 - формула скалярного квадрата.
- формула скалярного квадрата. , если вектор
, если вектор  векторы
векторы 

 -мерный случай.
-мерный случай.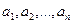 называется
называется  .
. -мерного вектора
-мерного вектора 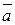 можно расположить либо в строку
можно расположить либо в строку  - вектор-строка либо в столбец
- вектор-строка либо в столбец  - вектор-столбец.
- вектор-столбец. называются равными, если их соответствующие координаты равны, т.е.
называются равными, если их соответствующие координаты равны, т.е. 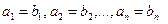 .
. .
.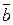 принадлежат
принадлежат  , координаты которого равны суммам соответствующих координат этих векторов:
, координаты которого равны суммам соответствующих координат этих векторов: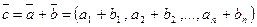 .
. - любое действительное число. Произведением вектора
- любое действительное число. Произведением вектора  .
. - переместительное свойство.
- переместительное свойство. - сочетательное свойство.
- сочетательное свойство. , где λ – действительное число.
, где λ – действительное число. , где λ и μ – действительные числа.
, где λ и μ – действительные числа. , где λ и μ – действительные числа.
, где λ и μ – действительные числа. .
. , что
, что  ,
,  .
.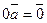 для любого вектора
для любого вектора  и
и  вектор
вектор  .
. и
и  , образует линейное подпространство
, образует линейное подпространство 


