
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Уравнение поверхности и линииСодержание книги
Поиск на нашем сайте Пусть в прямоугольной системе координат
Будем говорить, что соотношение (73) является уравнением поверхности Линию в пространстве можно рассматривать как пересечение двух поверхностей или множество точек, лежащих на двух поверхностях одновременно. Поэтому система двух уравнений типа (73)
Называют уравнением линии
Плоскость в пространстве Определение. Уравнение вида
Называется общим уравнением плоскости в системе координат
Пример. Составить уравнение плоскости с перпендикулярным вектором Решение. Согласно формуле (76) имеем:
Рассмотрим вопрос о взаимном расположении плоскостей в пространстве. Пусть две плоскости заданы уравнениями
Угол между плоскостями в пространстве. При любом положении двух плоскостей угол между ними равен углу φ между их нормальными векторами
Второй (смежный) угол равен Условие параллельности плоскостей. Если плоскости параллельны, то их нормальные векторы коллинеарны, и наоборот. В этом случае из формулы (
Условие перпендикулярности плоскостей. Если плоскости (77) перпендикулярны, то перпендикулярны между собой и их нормальные векторы. Так как
Расстояние от точки до плоскости. Пусть плоскость задана уравнением (75). Тогда расстояние от точки
6.2. Прямая в пространстве. Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе
При решении задач чаще используется другой вид уравнений прямой. Если прямая параллельна вектору
Уравнения (82) называются каноническими уравнениями прямой в пространстве.
Если прямая задана уравнениями общего вида (81), то переход к каноническим уравнениям осуществляется с помощью вычисления координат направляющего вектора
Пример. Найти уравнение прямой, заданной уравнениями общего вида
Решение. Сначала определим какую-либо точку
откуда
По формуле (82) находим каноническое уравнение прямой:
Уравнение прямой, проходящей через две данные точки
Угол между прямыми. Угол между прямыми в пространстве равен углу j между их направляющими векторами:
Условие параллельности прямых. Две прямые параллельны тогда и только тогда, когда их направляющие векторы коллинеарны. Поэтому из формулы
Условие перпендикулярности прямых. Прямые перпендикулярны тогда и только тогда, когда их направляющие векторы перпендикулярны. Из формулы (85) следует искомое условие:
Расстояние от точки до прямой. Пусть дана прямая, проходящая через точку
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.006 с.) |

 координаты
координаты 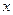 ,
,  и
и  связаны некоторым уравнением
связаны некоторым уравнением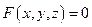 (73)
(73) в заданной системе координат, если ему удовлетворяют координаты любой точки
в заданной системе координат, если ему удовлетворяют координаты любой точки  , принадлежащей
, принадлежащей  (74)
(74) в пространстве, если этим уравнениям удовлетворяют только координаты точек, лежащих на линии
в пространстве, если этим уравнениям удовлетворяют только координаты точек, лежащих на линии  (75)
(75) . Вектор
. Вектор  перпендикулярен плоскости (75); он называется нормальным вектором этой плоскости. Если известно, что плоскость проходит через некоторую точку
перпендикулярен плоскости (75); он называется нормальным вектором этой плоскости. Если известно, что плоскость проходит через некоторую точку  , то такая плоскость может быть задана уравнением
, то такая плоскость может быть задана уравнением (76)
(76) , проходящей через точку
, проходящей через точку  .
. , или
, или 
 и
и  (77)
(77) и
и  . Следовательно по формуле
. Следовательно по формуле  , получаем, что угол φ между плоскостями (77) определяется по формуле
, получаем, что угол φ между плоскостями (77) определяется по формуле (78)
(78) .
. и
и 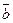 коллинеарны в том и только в том случае, если их координаты пропорциональны:
коллинеарны в том и только в том случае, если их координаты пропорциональны: ) получаем условие параллельности плоскостей, заданных уравнениями (77):
) получаем условие параллельности плоскостей, заданных уравнениями (77): (7)
(7) , из формулы (78) получаем условие перпендикулярности двух плоскостей:
, из формулы (78) получаем условие перпендикулярности двух плоскостей: (79)
(79) (80)
(80) (81)
(81) , называемому направляющим вектором, и проходит через точку
, называемому направляющим вектором, и проходит через точку 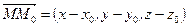 и
и  , где
, где  произвольная точка прямой. Тогда искомое уравнение прямой будет иметь вид:
произвольная точка прямой. Тогда искомое уравнение прямой будет иметь вид: (82)
(82) (83)
(83)
 , через которую проходит эта прямая. Положим
, через которую проходит эта прямая. Положим  , тогда из данных уравнений получаем систему для определения
, тогда из данных уравнений получаем систему для определения  и
и  :
:
 ,
,  . Координаты направляющего вектора находим по формуле (83):
. Координаты направляющего вектора находим по формуле (83): ,
, 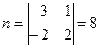 ,
, 
 .
. и
и  имеет вид
имеет вид (84)
(84) и
и  , т.е. вычисляется по формуле (78):
, т.е. вычисляется по формуле (78): (85)
(85) (86)
(86)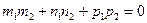 (87)
(87) , находящаяся вне этой прямой. Тогда расстояние
, находящаяся вне этой прямой. Тогда расстояние  от точки
от точки  до заданной прямой вычисляется по формуле:
до заданной прямой вычисляется по формуле: (88)
(88)


