
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение вектора в ортогональном базисе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим базис пространства
Ортогональные базисы хорошо представимы на плоскости и в пространстве.
Рассмотрим разложение произвольного вектора
Умножим обе части этого равенства, представляющие собой векторы, на вектор
Однако в силу взаимной ортогональности векторов базиса (24) все скалярные произведения векторов базиса, за исключением первого, равны нулю, т.е. коэффициент
Умножая поочередно равенство (25) на другие базисные векторы, получаем простую формулу для вычисления коэффициентов разложения вектора
Соотношения (26) имеют смысл, при Выделим особый случай ортогонального базиса, когда все векторы в (24) имеют единичную длину
4.5. Оператор линейного преобразования Матрица перехода от одного базиса к другому Пусть в векторном пространстве
Матрица
Матрица Пусть произвольный вектор
Найдем связь между координатами вектора
Система (30) представляет собой формулы пересчета координат вектора В матричной форме система соотношений (14) представима в виде
где
где Пример. Векторы Решение. Первоначально убедимся, что векторы
Связь между базисами выражается следующей системой уравнений:
Матрица перехода от базиса
Находим обратную матрицу
По формуле
Это означает, что вектор
Линейные операторы Определение. Отображение
Свойство (33) называется аддитивностью линейного отображения, а свойство (34) – однородностью этого отображения. В таком случае говорят, что задан линейный оператор Будем говорить, что Определение. Линейное отображение пространства Пусть
Применим линейный оператор
Поскольку
Подставляя формулы (36) в (35), получаем:
Группируя коэффициенты при базисных векторах
Пусть вектор
Тогда в силу единственности разложения вектора в данном базисе получаем путем приравнивания коэффициентов при базисных векторах в разложениях (36) и (37):
Матрица
где Таким образом, каждому линейному оператору Если матрицы Пример. В пространстве
Найти образ Решение. По формуле (40) получаем
Таким образом,
Для разных базисов матрицы одного и того же оператора будут разными. Связь между ними определяется теоремой. Теорема. Пусть линейный оператор
где Доказательство. Линейным оператором
Поскольку
Умножив равенство
или с учетом равенства
Подставляя выражение
Умножая последнее равенство слева на матрицу
Сравнивая последнее выражение с
Умножим обе части равенства на
получаем доказываемую связь между матрицами
Пример. В пространстве
Найти матрицу Решение. Матрица перехода имеет вид
Следовательно, по формуле (41) получаем:
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

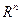 , в котором каждый вектор ортогонален остальным векторам базиса:
, в котором каждый вектор ортогонален остальным векторам базиса: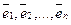 ,
, 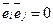 ,
,  ,
, 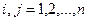 . (24)
. (24)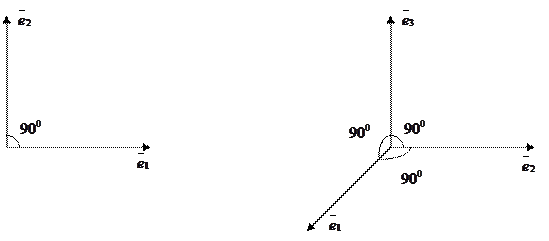
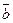 в ортогональном базисе (24). Составим разложение этого вектора с неизвестными пока координатами разложения в данном базисе:
в ортогональном базисе (24). Составим разложение этого вектора с неизвестными пока координатами разложения в данном базисе: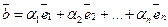 (25)
(25)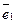 . В силу свойств 2 и 3 скалярного произведения векторов имеем
. В силу свойств 2 и 3 скалярного произведения векторов имеем .
.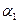 определяется по формуле
определяется по формуле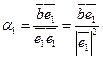
 (26)
(26)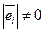 .
. или нормированы по своей длине. В таком случае базис называют ортонормированным, и координаты разложения (26) имеют наиболее простой вид:
или нормированы по своей длине. В таком случае базис называют ортонормированным, и координаты разложения (26) имеют наиболее простой вид:
 и
и  ,
,  . Представим каждый из векторов базиса
. Представим каждый из векторов базиса  (27)
(27)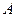 , составленная из коэффициентов разложения векторов базиса
, составленная из коэффициентов разложения векторов базиса 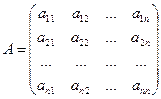 (28)
(28)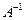 .
.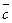 имеет координаты
имеет координаты  и
и  в базисах
в базисах 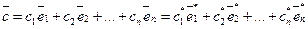 (29)
(29)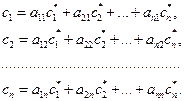 (30)
(30)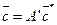 (31)
(31)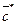 - векторы-столбцы координат вектора
- векторы-столбцы координат вектора  - транспонированная матрица
- транспонированная матрица  (32)
(32)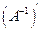 - транспонированная матрица
- транспонированная матрица 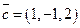 ,
, 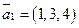 ,
, 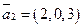 и
и 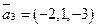 заданы в базисе
заданы в базисе 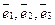 . Представить вектор
. Представить вектор  .
.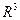 , для чего вычислим определитель, составленный из координат этих векторов:
, для чего вычислим определитель, составленный из координат этих векторов: .
.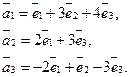
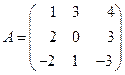 .
.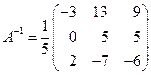 ,
,  .
. .
.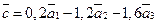
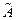 линейного пространства
линейного пространства  называется линейным отображением (гомоморфизмом или морфизмом), если для любых элементов
называется линейным отображением (гомоморфизмом или морфизмом), если для любых элементов 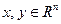 и любого числа a справедливы равенства
и любого числа a справедливы равенства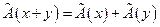 , (33)
, (33)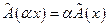 (34)
(34) является образом элемента
является образом элемента 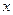 .
. по этому базису имеет вид:
по этому базису имеет вид: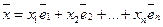 .
.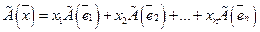 (35)
(35) также является вектором из
также является вектором из 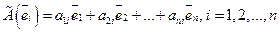 (36)
(36)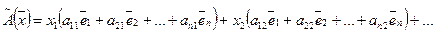
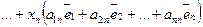
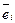 , получаем:
, получаем: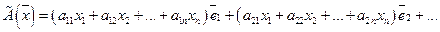
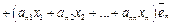 (37)
(37)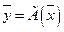 имеет в том же базисе
имеет в том же базисе 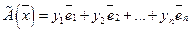 (38)
(38) (39)
(39)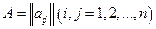 , составленная из коэффициентов при
, составленная из коэффициентов при 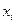 , называется матрицей оператора
, называется матрицей оператора 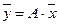 или
или 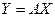 (40)
(40)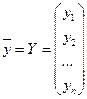 ,
,  .
. .
.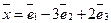 .
.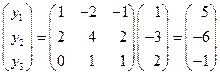
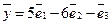 .
. соответственно в базисах
соответственно в базисах 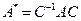 (41)
(41) - матрица перехода от базиса
- матрица перехода от базиса  пространства
пространства  этого же пространства, т.е. для обоих базисов справедливы равенства
этого же пространства, т.е. для обоих базисов справедливы равенства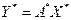 (42)
(42)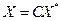 ,
,  (43)
(43)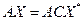
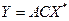
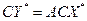
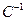 , получаем окончательную формулу
, получаем окончательную формулу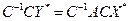
 .
.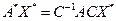
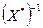 справа, и учитывая, что
справа, и учитывая, что 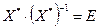 , получаем:
, получаем: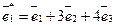 ,
, 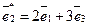 ,
, 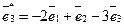 .
.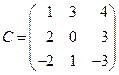 , а обратная к ней матрица
, а обратная к ней матрица 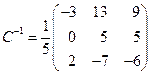 .
. .
.


