
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие линейной комбинации векторов. Линейная зависимость векторов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Угол между двумя векторами. Определение скалярного произведения и его основные свойства. Выражение скалярного произведения через координаты векторов в ортонормированном базисе. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. Пусть прямые l1 и l2 заданы уравнениями: Обозначим через φ1 угол наклона прямой l1 к оси Ох и через φ угол, на который нужно повернуть прямую l1 до совпадения с l2
Заметив, что tgφ1=k1 и tgφ2=k2 получим:
Скалярное произведение — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними. Обычно используется одно из следующих обозначений:
Свойства скалярного произведения 1. Скалярное произведение обладает переместительным свойством: ab=ba
5. Если векторы а и b(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^ b, то ab=0. Справедливо и обратное утверждение: если ab =0 и а¹ 0¹b, то а ^ b . В трёхмерном вещественном векторном пространстве векторов В любом евклидовом пространстве (размерности n) всегда можно выбрать ортонормированный базис при разложении векторов по которому:
скалярное произведение будет выражаться приведённой следующей формулой:
В таком же, но комплексном, пространстве, скалярное произведение вводится по несколько другой формуле:
6. Выражение скалярного произведения через координаты векторов в ортонормированном базисе. В трёхмерном вещественном векторном пространстве векторов В любом евклидовом пространстве (размерности n) всегда можно выбрать ортонормированный базис при разложении векторов по которому:
скалярное произведение будет выражаться приведённой следующей формулой:
В таком же, но комплексном, пространстве, скалярное произведение вводится по несколько другой формуле:
Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости. Пусть заданы точки должны быть компланарны, т.е.
Уравнение плоскости: Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости. Пусть заданы два вектора Уравнение плоскости: Понятие линейной комбинации векторов. Линейная зависимость векторов. Линейное пространство — это множество элементов, называемых векторами, над которыми определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых базисом линейного пространства. Количество векторов в базисе равно размерности пространства. Любой вектор из пространства можно представить, как линейную комбинацию базисных векторов. То есть, если у нас есть базис
Cумма вида
называется линейной комбинацией элементов Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля. Система векторов называется линейно зависимым если хотя бы 1 вектор системы можно представить как линейную комбинацию других векторов данной системы. Система векторов называется линейно независимым если не 1 из векторов системы нельзя представить как линейную комбинацию других векторов данной системы Бесконечное подмножество векторов из Число элементов максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом (базисом Га́меля или линейным базисом). Элементы базиса также называют базисными векторами. Свойства базиса: Любые Любой вектор
Система состоящая из 2 коллинеарных векторов линейно зависима. a,b – сонаправлены a= Система состоящая из 3 компланарных векторов линейно зависима. a,b,c – b= Понятие базиса. Разложение вектора по базису. Координаты вектора относительно данного базиса. Базис (др.-греч., основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов. Представление какого-то конкретного (любого) вектора Числовые коэффициенты Координатами вектора b относительно базиса В называется упорядоченная тройка чисел { x, y, z }, т.ч. b= x ·a1+ y ·а2+ z · а3. Обозначение: b={ x, y, z } B Любой вектор имеет однозначно определенные координаты относительно любого базиса. Базис на прямой, на плоскости, в пространстве. Выражение Пусть L, Р и S – прямая, плоскость и пространство точек соответственно и Определение. Базисом векторного пространства
Обозначение базиса Определение. Базисом векторного пространства
рис.1.
Определение. Базисом векторного пространства
рис.2.
Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 862; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.233 (0.012 с.) |



 ,
,  ,
, 


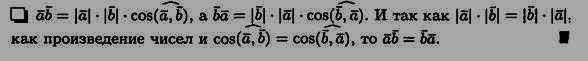


 введение скалярного произведения по формуле
введение скалярного произведения по формуле  превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).
превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).
 ,
, итд,
итд, .
. . Здесь через
. Здесь через 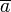 обозначено число, комплексно сопряжённое к
обозначено число, комплексно сопряжённое к  . При таком определении скалярное произведение становится положительно определённым.
. При таком определении скалярное произведение становится положительно определённым. ,
, 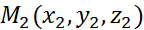 и вектор
и вектор  .Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору a. Векторы
.Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору a. Векторы 
 и вектор
и вектор 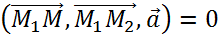

 , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы а,b,
, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы а,b,  должны быть компланарны.
должны быть компланарны.
 , то
, то  , где
, где 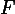 — это поле, над которым определенно линейное пространство
— это поле, над которым определенно линейное пространство  .
.
 с коэффициентами
с коэффициентами  .
. линейно независимых элементов
линейно независимых элементов  можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:
можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов: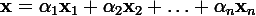 .
. b
b  , a,b – противоположено направлены a=
, a,b – противоположено направлены a= 
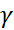 a+
a+  пространства в виде линейной комбинации векторов базиса (суммы базисных векторов числовыми коэффициентами), например
пространства в виде линейной комбинации векторов базиса (суммы базисных векторов числовыми коэффициентами), например 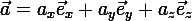 или
или  или, употребляя знак суммы
или, употребляя знак суммы  :
:  называется разложением этого вектора по этому базису.
называется разложением этого вектора по этому базису. называются коэффициентами разложения, а их набор в целом — представлением (или представителем) вектора
называются коэффициентами разложения, а их набор в целом — представлением (или представителем) вектора  (Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор).
(Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор). , где
, где  называется линейной комбинацией системы векторов
называется линейной комбинацией системы векторов  , а числа
, а числа  называются коэффициентами этой линейной комбинации.
называются коэффициентами этой линейной комбинации. . Тогда
. Тогда  – векторные пространства векторов как направленных отрезков на прямой L, на плоскости Р и в пространстве S соответственно.
– векторные пространства векторов как направленных отрезков на прямой L, на плоскости Р и в пространстве S соответственно. называется любой ненулевой вектор
называется любой ненулевой вектор  , т.е. любой ненулевой вектор коллинеарный прямой L:
, т.е. любой ненулевой вектор коллинеарный прямой L:  и
и  .
. – базис
– базис  называется любая упорядоченная пара неколлинеарных векторов пространства
называется любая упорядоченная пара неколлинеарных векторов пространства 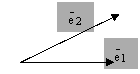
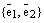 , где
, где  ,
,  – базис
– базис  .
. называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства
называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства 
 – базис
– базис 


