
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение линейного пространстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Множество I. Дано правило, указывающее, как для любых двух элементов II. Дано правило, указывающее, как для любого вещественного III. Определено понятие равенства элементов в IV. I и II операции называются соответственно сложением и умножением на число и удовлетворяют следующим восьми условиям: Сложение коммутативно
Сложение ассоциативно ( Умножение ассоциативно
4) умножение дистрибутивно по отношению к сложению элементов из
Умножение дистрибутивно по отношению к сложению чисел ( 6) существует такой элемент
для любого элемента 7) для любого элемента
8) для любого элемента
Если произведение Свойства линейного пространства
Основные примеры линейных пространств будут указаны ниже, а вначале приведем (без доказательства) простейшие свойства, которые непосредственно вытекают из определения линейного пространства. Свойство 1. В каждом линейном пространстве существует единственный Свойство 2. В каждом линейном пространстве для каждого вектора существует единственный противоположный вектор. Свойство 3. В любом линейном пространстве для всякого вектора имеет
В левой части равенства символ Свойство 4. Произведение любого числа
Свойство 5. Для каждого элемента – Если природа элементов, входящих в
Примеры конкретных линейных пространств Пример 1. Множество вещественных чисел по отношению к обычным операциям сложения и умножения чисел является вещественным линейным пространством. Пример 2. Множество всех свободных векторов в пространстве представляет собой линейное пространство, ибо все аксиомы IV пункта выполнены (операции сложения векторов по правилу параллелограмма и умножения вектора на число определены обычным образом). Пример 3. Пусть
и
означают два решения некоторой системы линейных однородных уравнений
Ранее было показано, что их сумма
и произведение любого из них (для определенности
также будут решениями системы (1.16). Нетрудно показать, что множество всех решений однородной системы (1.16) является линейным пространством, у которого нулевым элементом является элемент О (0, 0,..., 0), а противоположным для элемента ( Пример 4. Множество а = ( b = ( считаются различными, если нарушено хотя бы одно из равенств
Операции сложения элементов элемента
Если в качестве нулевого элемента возьмем совокупность Пример 5. Множество всех многочленов
Пример 6. Множество всех непрерывных функций от одной переменной Линейная зависимость
При изучении векторной алгебры было введено понятие линейной комбинации векторов. Обобщим это понятие на случай линейного пространства. Пусть Определение 1. Линейной комбинацией векторов
Числа Определение 2. Векторы
Если же равенство (2.18) возможно только в единственном случае, когда
то векторы Пример 1. Обратимся к линейному пространству Элементы пространства
образуют в этом пространстве линейно независимую систему. Линейная независимость системы (1.19) следует из того, что соотношение
может быть выполнено для любого
Пример 2. В линейном пространстве, элементами которого являются свободные векторы на плоскости, любые три вектора
Пример 3. Функции
выполняется тождественно, если положить Теорема. Если векторы
или, поделив обе части последнего равенства на
Ясно, что верно и обратное утверждение. Последнее равенство называется разложением вектора
Базис и координаты
Определение 1. Система
где Теорема. Коэффициенты Доказательство. Действительно, допустим напротив, что для вектора
Вычитая почленно из первого равенства второе, будем иметь
Но так как векторы
откуда и следует единственность представления вектора
либо в виде столбца
который называют координатным столбцом. Рассмотрим примеры. Пример 1. В множестве всех свободных векторов в пространстве тройка единичных взаимно ортогональных векторов Пример 2. В линейном пространстве многочленов
образуют базис. Координатами всякого многочлена
в этом базисе являются его коэффициенты Во всяком фиксированном базисе Размерность
Определение 1. Линейно пространство Иногда, чтобы указать размерность пространства пишут Рассмотрим примеры. Пример 1. Множество всех свободных векторов на плоскости является двумерным линейным пространством, а множество всех свободных векторов в пространстве является трехмерным линейным пространством. Пример 2. Линейное пространство многочленов Определение 2. Линейное пространство Подпространства
Определение 1. Подпространством линейного пространства Рассмотрим примеры. Пример 1. В линейном пространстве свободных векторов на плоскости множество всех векторов, параллельных какой-либо прямой, является подпространством. Пример 2. В пространстве векторов, элементами которого являются одностолбцовые матрицы
где
образует линейное подпространство. Это следует из того, что сумма решений системы (1.21) и произведения решения на любое вещественное число являются также ее решениями. Пример 3. Множество всех многочленов Пример 4. Нулевой вектор линейного пространства Пример 5. Само линейное пространство Отметим два свойства подпространств: Свойство 1. Размерность любого подпространства в Свойство 2. Если в
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 726; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.208.243 (0.009 с.) |

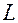 называется линейным (векторным) пространством, если:
называется линейным (векторным) пространством, если: ,
, 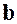 из
из  и любого элемента
и любого элемента 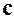 =
= 
 , называемый нулевым, что
, называемый нулевым, что ,
,  .
. )
) )
) . (1.16)
. (1.16) )
)
 ,
,  , …,
, …,  )
) , элементами которого служат упорядоченные совокупности
, элементами которого служат упорядоченные совокупности  произвольных вещественных чисел
произвольных вещественных чисел  )
) )
) .
. ;
; .
. , будет элемент
, будет элемент  , то справедливость условий IV пункта устанавливается элементарной проверкой каждого из них.
, то справедливость условий IV пункта устанавливается элементарной проверкой каждого из них. от одной переменной
от одной переменной  , степень которых меньше либо равна заданному числу
, степень которых меньше либо равна заданному числу  из
из  , которое обозначают символом
, которое обозначают символом  , так как для любых непрерывных на
, так как для любых непрерывных на  функций
функций  и
и 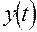 их сумма
их сумма  является линейным пространством.
является линейным пространством. означают произвольные векторы линейного пространства
означают произвольные векторы линейного пространства  , т. е. вектор
, т. е. вектор . (1.17)
. (1.17)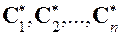 не все равные нулю, такие, что выполняется равенство
не все равные нулю, такие, что выполняется равенство . (1.18)
. (1.18) ,
, называются линейно независимыми.
называются линейно независимыми.  (1.19)
(1.19)
 .
. линейно зависимы, т. е. существуют такие числа
линейно зависимы, т. е. существуют такие числа  , не равные нулю одновременно, что выполняется соотношение
, не равные нулю одновременно, что выполняется соотношение .
. линейно зависимы, так как соотношение
линейно зависимы, так как соотношение
 .
. , то
, то
 получим
получим .
. по векторам
по векторам  .
.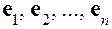 линейного пространства
линейного пространства  , (1.20)
, (1.20) означают коэффициенты линейной комбинации.
означают коэффициенты линейной комбинации. ;
; .
. .
. ,
, либо
либо  , либо
, либо  ,
, ,
,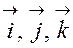 образует базис. Координатами вектора
образует базис. Координатами вектора  относительно этого базиса служат проекции вектора
относительно этого базиса служат проекции вектора 
 .
. .
.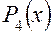 степень которых не выше 4, является пятимерным.
степень которых не выше 4, является пятимерным. ,
, – любые вещественные числа, множество векторов, удовлетворяющих системе однородных линейных уравнений
– любые вещественные числа, множество векторов, удовлетворяющих системе однородных линейных уравнений (1.21)
(1.21)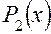 , степень которых не больше двух, является подпространством в пространстве всех многочленов
, степень которых не больше двух, является подпространством в пространстве всех многочленов  -мерном подпространстве
-мерном подпространстве  , то всегда можно дополнительно так выбрать векторы
, то всегда можно дополнительно так выбрать векторы  , что система векторов
, что система векторов  образует базис в
образует базис в 


