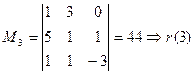Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Размерность и базис линейного пространстваСодержание книги Поиск на нашем сайте
Линейное пространство - n -мерное, если в нем существует система из n-линейно независимых векторов, а любая система из (n +1) векторов является линейно зависимой, таким образом размерность линейного пространства - это наибольшее количество линейно независимых элементов в нем. Базисом n -мерного линейного пространства Напр.: базис
Опр.: Вектора некомпланарные, если они не лежат в одной плоскости.
Иными словами множество из n- векторов называется базисом, если оно линейно независимо и любой вектор этого пространства можно представить как линейную комбинацию базисных векторов. Th1: Система из n -единичных векторов в пространстве Th2: Любой вектор пространства
Пр.: Образует ли
Ранг матрицы. Если дана некоторая система n- мерных векторов, то возникает вопрос, является ли эта система линейно зависимой или нет. При поверхностном взгляде на это вопрос трудно ответить, например, пусть дана система векторов а1=(2,-5,1,-1), а2=(1,3,6.5), а3=(-1,4,1,2). Эти векторы связаны соотношением 7а1-3а2+11а3=0. Рассмотрим произвольную матрицу, содержащую m строк и n столбцов.
Столбцы этой матрицы, рассматриваемые как m -мерные векторы, могут быть линейно зависимыми. Ранг системы столбцов, т.е. максимальное число линейно независимых столбцов матрицы А называется рангом матрицы А. Подобным образом строки матрицы А можно рассматривать как n-мерные векторы. Оказывается, ранг системы строк матрицы А равен рангу системы столбцов, т.е. рангу этой матрицы. Доказательство этого весьма неожиданного утверждения будет получено после того, как мы введем еще одну форму определения ранга матрицы А. Опр.: Выделим в матрице А k строк и k столбцов; элементы матрицы, стоящие на пересечении выделенных строк и столбцов, являются элементами определителя k –го порядка, который называется минором матрицы k–го порядка. Пример:
М1-любой элемент матрицы.
М4=0, так как есть 3 строки, а 4 строка – нулевая. Среди всех миноров матриц различных порядков есть миноры, равные нулю, есть миноры, отличные от нуля. Теорема: Наивысший порядок отличного от нуля минора, называется рангом матрицы [ r (A)]. Доказательство: Пусть наивысший порядок отличных от нуля миноров матрицы A равен r и пусть он (минор r -го порядка D) расположен в левом верхнем углу матрицы А и отличен от нуля.
Тогда первые r столбцов матрицы А будут линейно независимыми: если бы между ними существовала линейная зависимость, то по свойствам определителей этот определитель был бы равен нулю. Докажем теперь, что всякий l -й столбец матрицы А, r<l<=n, будет линейной комбинацией первых r векторов. Берем любое i<=i<=m, и строим вспомогательный определитель (r +1) порядка.
Рассмотрим алгебраические дополнения элементов последней строки определителя
Таким образом, в системе столбцов матрицы А мы нашли максимальную линейно независимую подсистему, состоящую из r столбцов, что доказывает, что ранг матрицы А равен r. Эта теорема дает метод для практического вычисления ранга матрицы, а поэтому и для решения вопроса о существовании линейной зависимости в данной системе векторов; составляя матрицу, для которой данные векторы служат столбцами, и вычисляя ранг этой матрицы, мы находим максимальное число линейно независимых векторов нашей системы.
Правило вычисления ранга матрицы: При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор k -го порядка D, отличный от нуля, то требуют вычисления лишь миноры (k +1) –го порядка, окаймляющие минор D: если все они равны нулю, то ранг матрицы равен k. Пр.:
Из определения ранга матрицы следует утверждение: 1. 0 ≤ r ≤ min (m,n) 2. r = 0, тогда и только тогда, когда матрица нулевая 3. для квадратной матрицы порядка n, r=n, тогда и только тогда, когда матрица не особенная. Пример: Найти максимальную линейно независимую подсистему в системе векторов а1 =(2,-2,-4), а2= (1,9,3), а3= (-2,-4,1), а4 =(3,7,-1).
Элементарные преобразования матриц: 1. Транспонирование – строки меняются местами со столбцами; 2. Перестановка двух строк или столбцов; 3. Умножение элементов некоторой строки или столбца на λ, где λ≠0; 4. Прибавление к элементам какой-либо строки или столбца элементы другой строки или столбца, предварительно умноженные на некоторое число. Th: Элементарные преобразования ранга матрицы не меняют. Так как ранг – наивысший порядок отличного от нуля минора (т.е. является определителем), то по свойствам определителей преобразование 1. величины определителя, а соответственно и минора, не меняет. Преобразование 2. меняет знак минора на противоположный. Преобразование 3. увеличивает величину минора в λ-раз Преобразование 4. величину минора (определителя) не меняет. Следовательно, в результате перечисленных преобразований, миноры неравные нулю, останутся неравными нулю, а миноры, равные нулю, остаются равными нулю. Это означает, что ранг матрицы не меняется. Пример:
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.186 (0.009 с.) |

 является любая упорядоченная систем n -мерного независимых векторов в нем.
является любая упорядоченная систем n -мерного независимых векторов в нем. - образуют тройка некомпланарных векторов.
- образуют тройка некомпланарных векторов. образует базис
образует базис в любом пространстве
в любом пространстве  - базис?
- базис? по базису
по базису




 и
и  - линейно независимы
- линейно независимы


 - координаты
- координаты 
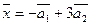


 =***
=***

 , получающийся «окаймлением» минора D соответствующими элементами l -го столбца и i -ой строки. При любом i определитель
, получающийся «окаймлением» минора D соответствующими элементами l -го столбца и i -ой строки. При любом i определитель  равен нулю. Действительно, если i>r, то
равен нулю. Действительно, если i>r, то  будет минором (r +1) порядка нашей матрицы А и поэтому будет равен нулю в виду выбора числа r. Если же i<=r, то
будет минором (r +1) порядка нашей матрицы А и поэтому будет равен нулю в виду выбора числа r. Если же i<=r, то  Алгебраическим дополнением для элемента
Алгебраическим дополнением для элемента  служит определитель D. Если же 1 <=j<=r, то алгебраическим дополнением для элемента
служит определитель D. Если же 1 <=j<=r, то алгебраическим дополнением для элемента  в
в  будет число
будет число ; оно не зависит от i и поэтому обозначено через
; оно не зависит от i и поэтому обозначено через  . Разлагая определитель
. Разлагая определитель  , мы получим:
, мы получим: , откуда, так как
, откуда, так как 
 . Это равенство справедливо при всех i от 1 до m, а так как его коэффициенты от i не зависят, то мы получаем, что весь i -й столбец матрицы А будет суммой ее первых r столбцов, взятых с коэффициентами
. Это равенство справедливо при всех i от 1 до m, а так как его коэффициенты от i не зависят, то мы получаем, что весь i -й столбец матрицы А будет суммой ее первых r столбцов, взятых с коэффициентами  .
.