
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Произвольная система линейных уравнений.Содержание книги Поиск на нашем сайте
А – матрица СЛУ В – расширенная матрица СЛУ Тh: Кронекера - Капелли Для того чтобы произвольная система линейных уравнений была совместна, необходимо и достаточно, чтобы r(A)=r(B). Примечание: r(A) ≤ r(B). Доказательство: (необходимость) Дано: Система совместна. Доказать: r(A)=r(B) Так как система совместна, то существует совокупность значений неизвестных
Рассмотрим расширенную матрицу В
Первый столбец умножим на (-с1), второй – на (-с2), и так далее – n-столбец умножим на (-сn) и сложим с последним столбцом. При этом ранг матрицы не изменится.
Имеем, что r(B)=r(B1), r(B1)=r(А), следовательно, r(B)=r(А). (достаточность) Дано: r(A)=r(B)=r Доказать, что система совместна. Согласно r(A)=r(B)=r, наивысший порядок отличного от нуля минора равен r. Для определенности предположим, что этот минор расположен в левом верхнем углу матрицы А. Тогда систему можно переписать в следующем виде:
Тогда последние (m-r) (т.к. ранг матрицы равен r) уравнений являются следствием первых r уравнений, их можно опустить. Тогда система перепишется в виде:
Возможны 2 случая: 1. r=n (ранг матрицы равен числу неизвестных), тогда система примет вид:
Определителем этой системы является минор r -того порядка, который по условию не равен нулю, так как r(A)=r(B)=r
Следовательно, по т. Крамера эта система совместна и имеет единственное решение. 2. r <n, т.е ранг матрицы меньше числа неизвестных, тогда система имеет вид:
Назовем x1, x2…xr - базисными переменными, xr+1, xr+2…xn - свободными переменными. Присваивая свободным переменным произвольные значения(xr+1=c1, xr+2=c2,…,xn=cn-r), мы получаем систему, в которой определитель Mr Вывод: при исследовании произвольной системы линейных уравнений, имеем следующие случаи: 1. r (A) 2. r (A) =r (B)=n – СЛУ имеет 1 (единственное) решение. 3. r (A) = r (B) < n – СЛУ имеет множество решений. Лекция 4 Векторная алгебра. Опр.: Векторной величиной называется всякая величина, обладающая направлением. Скалярной величиной называется всякая величина, не обладающая направлением. Например, сила, действующая на материальную точку, есть векторная величина. Скорость материальной точки – векторная величина. Температура тела – скалярная величина, так как с этой величиной не связано никакое направление. Масса и плотность тела – тоже скалярные величины.
Опр.: Вектор - направленный отрезок. А В - конец вектора. Длина вектора – его модуль, обозначается Единичный вектор – вектор, длина которого равна единице. Векторы, лежащие на параллельных прямых, называются коллинеарными. Нулевой вектор коллинеарен с любым вектором. Коллинеарные векторы, имеющие одинаковые направления и длины, называются равными. Два вектора, имеющие равные модули, и противоположные по направлению, называются противоположными. Действия над векторами. Опр. Суммой векторов a и b называется вектор с, полученный следующим образом:
OM=OL+LM, c=a+b, т.е. с равен сумме векторов a и b – правило треугольника.
Свойства: 1. 2.
Правило параллелограмма:
Если слагаемые a и b не коллинеарны, то сумму векторов a и b можно найти следующим способом: из любой точки строим векторы a = ОА и b=OB и достраиваем до параллелограмма OACB. Вектор с=ОС и есть сумма a и b.
Вычитание векторов: Вычесть вектор a 1 (вычитаемое) из вектора a2 (уменьшаемое) значит найти новый вектор x (разность), который в сумме с вектором a 1 даст вектор a2. Умножение вектора на число.
Произведение что и вектор Свойства умножения вектора на число: 1. 2. 3. Проекция вектора В пространстве заданы вектор
В
n А1 В1
Алгебраической проекцией Очевидно, что если угол
Th: (о проекциях). Th1: пр 1.
n А1 В1 прn 2.
В
А
n В1 А1
3.
Th2: (1) (2)
Th3:
M1 M2 M3
Координаты вектора. Действия над векторами в координатной форме. Рассмотрим в пространстве декартову прямоугольную систему координат. Радиус-вектором т. М называется вектор
Z
z x o y Y
X
Координаты вектора называются проекции вектора на координатные оси и обозначаются
Обозначим через
Координаты единичного вектора равны его направляющим косинусам:
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.188.141 (0.01 с.) |




 , которые при подстановке обращает каждое уравнение в тождество.
, которые при подстановке обращает каждое уравнение в тождество. ;
; 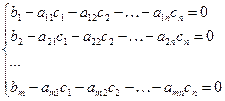 (*)
(*)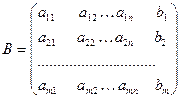
 (в силу соотношения (*))
(в силу соотношения (*))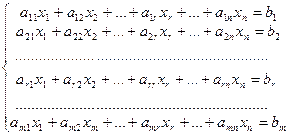



 ;
; ;
; 0 (по условию)
0 (по условию)  система совместна, но имеет множество решений.
система совместна, но имеет множество решений. В, А - начало вектора.
В, А - начало вектора. или
или  . Начало вектора называется точкой приложения. Нулевой вектор – вектор, начало и конец которого совпадают, его направление не определено.
. Начало вектора называется точкой приложения. Нулевой вектор – вектор, начало и конец которого совпадают, его направление не определено.






 +(-
+(-  =
=  , называется
, называется  и направленный в противоположную сторону, если
и направленный в противоположную сторону, если  и имеющий длину
и имеющий длину  .
. ,
,  є R.
є R. ,
, 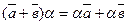
 на ось n.
на ось n. и ось n. Пусть А1 - проекция точки А на ось n, В1 – проекция точки В на ось n.
и ось n. Пусть А1 - проекция точки А на ось n, В1 – проекция точки В на ось n.

 А
А
 - острый, т.е. направление вектора А1В1 совпадает с направлением оси n, то пр.n
- острый, т.е. направление вектора А1В1 совпадает с направлением оси n, то пр.n 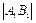 , а если
, а если  cos
cos 
 В
В



 А С
А С





 С
С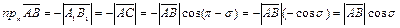
 ,
,  , но, с другой стороны,
, но, с другой стороны, , следовательно,
, следовательно, 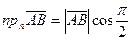

 , (т.е.
, (т.е.  направлены в одну сторону), то
направлены в одну сторону), то 
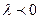 , то есть
, то есть 





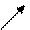


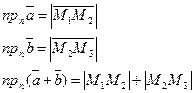 , но по чертежу
, но по чертежу  , следовательно,
, следовательно, , точка приложения которого совпадает с началом координат.
, точка приложения которого совпадает с началом координат.
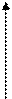










 M
M - радиус-вектор т. М.
- радиус-вектор т. М.

 углы, образуемые вектором
углы, образуемые вектором  с координатными осями. Косинусы этих углов называются направляющим косинусами вектора, т.е.
с координатными осями. Косинусы этих углов называются направляющим косинусами вектора, т.е. 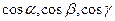 - направляющие косинусы вектора
- направляющие косинусы вектора  , тогда
, тогда (
( - квадрат длины диагонали прямоугольного параллелепипеда).
- квадрат длины диагонали прямоугольного параллелепипеда).




