
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многомерное линейное (векторное) пространствоСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Всякая точка на плоскости определяется двумя координатами, т.е. упорядоченной системой из двух действительных чисел, всякий вектор на плоскости определяется двумя компонентами. Аналогично, всякая точка трехмерного пространства определяется тремя координатами, всякий вектор в пространстве – тремя компонентами. Для определения шара в пространстве нужно задать координаты его центра и радиус, т.е. четыре действительных числа, следовательно, целесообразно рассмотреть совокупность всевозможных упорядоченных чисел. Опр.: n-мерным вектором называется упорядоченный набор из n вещественных чисел а=(х1,х2…хп), где х1,х2…хп - координаты вектора. Действия: 1. 2 вектора равны, если равны их соответствующие координаты. 2. 3. 4.Дана система из m n -мерных векторов:
Рассмотрим множество Введем в V операцию сложения и умножения элементов множества V на действительные числа: 1. x+y=z, x,y,z 2. x∙α=z, х Также потребуем, чтобы операция сложения и умножения на число удовлетворяли следующим аксиомам: (1) x+y=y+x (2) (x+y)+z=x+(y+z) (3) Существует нулевой элемент, который в сумме с любым элементом дает тот же элемент (4) Существует противоположный элемент: x+(-x)=0, x (5) 1∙x=x, x (6) α(β∙x)=(α∙β)x, α,β (7) (8) В случае, когда заданы операция сложения и умножения на число и выполнены 8 аксиом, говорят, что задано линейное пространство (V) Примеры: 1. Множество векторов 2. Множество всех матриц размерностью Линейная зависимость Вектор b из n-мерного пространства называется пропорциональным вектору а, если существует такое число k, что b=k*a. Нулевой вектор пропорционален любому вектору в виду равенства 0=0*a. Обобщением понятия пропорциональности векторов служит понятие линейной комбинации векторов.
Опр.(*) Система векторов Опр. (**) Система векторов Замечание: система из одного ненулевого вектора – линейно независимая, так как Система из одного вектора линейно зависимо, тогда и только тогда, когда Теорема: Определения (*) и (**) равносильны. Пусть система векторов Обратно: пусть система линейно зависима в смысле определения (**), тогда Теорема: Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима. Док-во: Пусть Из этой теоремы следует: всякая система векторов, содержащая два равных, или два пропорциональных, а также всякая система, содержащая нулевой вектор, линейно зависимая. А также если система векторов Возникает вопрос, как много векторов может содержать линейно независимая система n -мерных векторов и существуют ли, в частности, такие системы с произвольно большим числом векторов. Рассмотрим в n -мерном пространстве векторы
называемые единичными векторами этого пространства. Пусть Всякие s векторов n -мерного векторного пространства составляют при s>n линейно зависимую систему.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.14.12 (0.007 с.) |


 =
= 

 Вектор
Вектор  , где
, где  - скаляры, называют линейной комбинацией векторов
- скаляры, называют линейной комбинацией векторов 
 и множество R действительных чисел.
и множество R действительных чисел. V
V


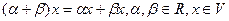
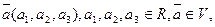 в этом случае множество векторов являющихся линейным пространством
в этом случае множество векторов являющихся линейным пространством - линейное пространство
- линейное пространство выполняется хотя бы при одном
выполняется хотя бы при одном  . Если же это соотношение выполняется только лишь в случае
. Если же это соотношение выполняется только лишь в случае  , то система называется линейно независимой.
, то система называется линейно независимой. тогда и только тогда, когда
тогда и только тогда, когда  .
.
 , следовательно,
, следовательно,  , следовательно,
, следовательно,  , т.е. система линейно зависима всмысле определения (**).
, т.е. система линейно зависима всмысле определения (**). , тогда
, тогда 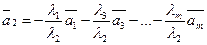 , следовательно,
, следовательно,  , где
, где  - скаляры. Следовательно,
- скаляры. Следовательно,  представлен в виде линейной комбинации остальных векторов, следовательно, система линейно зависима в смысле определения (*).
представлен в виде линейной комбинации остальных векторов, следовательно, система линейно зависима в смысле определения (*). из системы
из системы  , в котором не все коэффициенты равны нулю. Отсюда следует соотношение
, в котором не все коэффициенты равны нулю. Отсюда следует соотношение  ?, т.е. система
?, т.е. система 
 Так как левая часть этого равенства равна вектору (
Так как левая часть этого равенства равна вектору ( , то (
, то ( , т.е.
, т.е.  i=1,2,…,n, так как все компоненты нулевого вектора равны нулю, а равенство векторов равносильно равенству их соответствующих компонент. Таким образом, в n -мерном пространстве существует одна линейно независимая система, состоящая из n векторов.
i=1,2,…,n, так как все компоненты нулевого вектора равны нулю, а равенство векторов равносильно равенству их соответствующих компонент. Таким образом, в n -мерном пространстве существует одна линейно независимая система, состоящая из n векторов.


