
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декартова система координат на плоскости и в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Декартова система координат на плоскости и в пространстве. Декартова система координат в пространстве
Декартова система координат на плоскости Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы. Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.
Стандартным образом декартова система координат обозначаетсяOxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).
Понятие вектора. Линейные операции над векторами. Величины, которые полностью определяются заданием их числовых значений (например, длина, площадь, масса, объем и т.д.), называются скалярными. Величины, для определения которых, кроме числового значения, необходимо знать еще и направление (например, сила, скорость, ускорение и т.д.), называются векторными. Векторные величины геометрически изображаются с помощью векторов. Вектором называется направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Длиной вектора называется расстояние между началом и концом этого вектора и обозначается а) коллинеарны, б) одинаково направлены, в) имеют одинаковые длины. Вектор можно переносить в любую точку пространства посредством параллельного переноса (это следует из определения равенства векторов). Векторы в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Под линейными операциями над векторами понимают а) произведение вектора на число, б) сложение и вычитание векторов.
б) вектор ƛ
\
Координаты вектора. Действия над векторами, заданными своими координатами.
Линейные операции над матрицами. Умножение матриц.
Перестановки.
Определитель n–го порядка и его свойства.
Обратная матрица. Ранг матрицы.
Системы линейных уравнений
Метод Крамера. Матричный метод решения систем.
19. Критерий совместности систем линейных уравнений. Метод Гаусса
Взаимное расположение двух прямых, двух плоскостей, прямой и плоскости. Квадратичные формы.
Координаты вектора Теорема. Если
Группируя слагаемые, получим
Отсюда следует, что
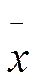 по базису по базису  . Это выражение можно записать в матричной форме . Это выражение можно записать в матричной форме  
Числа Если вектор Пример 7.Пусть V - пятимерное линейное пространство с базисом
Аналогично Справедливы следующие утверждения: 1. Вектор является нулевым вектором пространства тогда и только тогда, когда все его координаты в любом базисе равны нулю. 2. Координаты суммы двух векторов в некотором базисе равны сумме соответствующих координат этих векторов в том же базисе. 3. Координаты произведения вектора на число в некотором базисе равны произведению соответствующих координат данного вектора в том же базисе на это число. Два вектора равны между собой тогда и только тогда, когда равны между собой их соответствующие координаты в одном и том же базисе.
№ 37. Преобразование координат вектора при изменении базиса
Пусть в линейном пространстве V заданы два произвольных базиса Чтобы выразить векторы базиса Пусть
которые называются матрицами перехода от одного базиса к другому. Из соотношений и следует, что Пусть
Выясним, как преобразуются координаты вектора при переходе от одного базиса к другому. Подставим в выражение
Сравним полученное выражение с выражением. Коэффициенты при
Аналогично В матричной форме формулы и запишутся в виде
где
Евклидово пространство. Для того, чтобы в линейном пространстве можно было измерять длины и углы, вводят новую операцию – скалярное произведение. Пусть Аксиома 13.1. Скалярное произведение векторов коммутативно: Аксиома 13.2. Скалярное произведение векторов дистрибутивно относительно сложения векторов: Аксиома 13.3. Числовой множитель можно вынести за знак скалярного произведения: Аксиома 13.4 Скалярный квадрат вектора неотрицателен: Линейное пространство размерности n со скалярным произведением, удовлетворяющим аксиомам (13.1)-(13.4), называется n -мерным евклидовым пространством и обозначается Пример 3. 1. Евклидовым пространством является множество всех векторов 2. Евклидовым пространством является множество Т функций, непрерывных на отрезке 3. Если в арифметическом линейном пространстве Определение13. Величиной угла между двумя векторами
Матрица линейного оператора
Пусть f - линейный оператор некоторого пространства, переводящий базисные векторы Тогда
Определение 8. Матрица A = называется матрицей линейного оператора в базисе
Заметим, что в i -м столбце матрицы А стоят координаты Таким образом, каждому линейному оператору соответствует матрица оператора в данном базисе. Справедливо и обратное: всякой матрице порядка n соответствует линейный оператор n -мерного пространства. Соотношение можно записать в матричном виде Пример2.Найдём матрицу оператора из предыдущего примера:
Значит, искомая матрица имеет вид
Декартова система координат на плоскости и в пространстве. Декартова система координат в пространстве
Декартова система координат на плоскости Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы. Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.
Стандартным образом декартова система координат обозначаетсяOxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.7.116 (0.012 с.) |

 Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.
Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.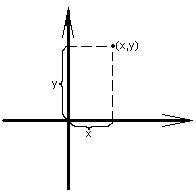 Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.
Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось. Вектор, длина которого равна нулю, называется нулевым вектором. Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором. Векторы
Вектор, длина которого равна нулю, называется нулевым вектором. Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором. Векторы  и
и  называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; записывают
называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; записывают  ||
||  . Нулевой вектор считается коллинеарным любому вектору. Два вектора называются равными, если они
. Нулевой вектор считается коллинеарным любому вектору. Два вектора называются равными, если они
 Произведением вектора
Произведением вектора  называется вектор удовлетворяющий следующим условиям:а)длина вектора равна произведению модуля числа ƛ на длину вектора ƛ
называется вектор удовлетворяющий следующим условиям:а)длина вектора равна произведению модуля числа ƛ на длину вектора ƛ  : |ƛ
: |ƛ  .
.


















 \
\

























 – базис линейного пространства, то для любого вектора
– базис линейного пространства, то для любого вектора 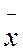 этого пространства существует единственная система чисел
этого пространства существует единственная система чисел  такая, что
такая, что  .
. Из теоремы 12.2 следует существование такой системы
Из теоремы 12.2 следует существование такой системы  , что выполняется. Докажем единственность. Допустим, что существует другая система
, что выполняется. Докажем единственность. Допустим, что существует другая система  , такая, что
, такая, что  . Тогда
. Тогда  .
. .
. , поскольку векторы
, поскольку векторы  линейно независимы. Теорема доказана.
линейно независимы. Теорема доказана. 
 называются координатами вектора
называются координатами вектора  в базисе
в базисе  .
. имеет в некотором базисе координаты
имеет в некотором базисе координаты  , то пишут
, то пишут  .
.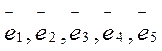 . Найти координаты векторов
. Найти координаты векторов  и
и  .
. , т.е.
, т.е.  имеет координаты (2,0,-1,3,0).
имеет координаты (2,0,-1,3,0). и
и  . Выразим векторы
. Выразим векторы  через
через  . Пусть
. Пусть  , где
, где  - координаты вектора
- координаты вектора  в базисе
в базисе  .
. через
через  , нужно решить систему уравнений относительно векторов
, нужно решить систему уравнений относительно векторов  . Эта система имеет единственное решение, поскольку её определитель отличен от нуля.
. Эта система имеет единственное решение, поскольку её определитель отличен от нуля.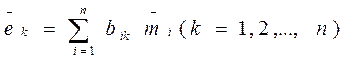 –
–  и
и  составим матрицы:
составим матрицы:
 .
. – произвольный вектор пространства V, который в базисе
– произвольный вектор пространства V, который в базисе  имеет координаты
имеет координаты 
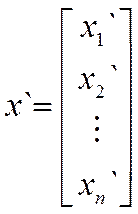
 , а в базисе
, а в базисе  –
–  , т. е.
, т. е. ;
; .
. .
. должны быть равны
должны быть равны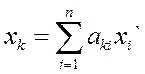

 ,
, ;
;  .
. –
–  и
и  ставится в соответствие действительное число
ставится в соответствие действительное число 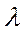 – их скалярное произведение, обозначаемое
– их скалярное произведение, обозначаемое  , удовлетворяющее следующим аксиомам.
, удовлетворяющее следующим аксиомам.
 .
. .
. , причём
, причём  тогда и только тогда, когда
тогда и только тогда, когда  .
.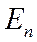 .
. обычного трёхмерного пространства. Скалярное произведение вводится так же, как в лекции 2, т. е. как произведение длин этих векторов на косинус угла между ними.
обычного трёхмерного пространства. Скалярное произведение вводится так же, как в лекции 2, т. е. как произведение длин этих векторов на косинус угла между ними. . Скалярное произведение функций f и φ определим так:
. Скалярное произведение функций f и φ определим так:  . Выполнение аксиом (13.1)-(13.4) непосредственно проверяется.
. Выполнение аксиом (13.1)-(13.4) непосредственно проверяется. скалярное произведение векторов
скалярное произведение векторов 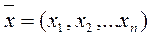 и
и  задать равенством
задать равенством  , то аксиомы (13.1)-(13.4) выполняются.
, то аксиомы (13.1)-(13.4) выполняются. и
и  называется угол
называется угол  такой, что
такой, что  , где
, где  норма вектора
норма вектора  .
. в
в  ;
; ,.
,. .
.
 .
.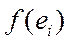 в базисе
в базисе  .
. .
.

 .
. 



