Взаимное расположение прямой и плоскости в пространстве.

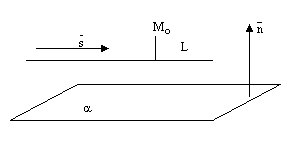
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

рис.6.

рис.7.

рис.8.

Теорема. Пусть плоскость задана общим уравнением

,

а прямая L задана каноническими уравнениями

или параметрическими уравнениями

, ,

в которых – координаты нормального вектора плоскости , – координаты произвольной фиксированной точки прямой L, –

координаты направляющего вектора прямой L. Тогда:

1) если , то прямая L пересекает плоскость в точке, координаты которой можно найти из системы уравнений

; (7)

2) если и , то прямая лежит на плоскости;

3) если и , то прямая параллельна плоскости.

Доказательство. Условие говорит о том, что вектроры и не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.

Если , то это означает, что . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка . Если , то точка – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.

Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.

Теорема доказана.

 

26. Эллипс.

Эллипсом называется такое множество точек плоскости, что сумма расстояний от любой точки этого множества до двух данных точек плоскости есть величина постоянная, большая расстояния между данными точками. Данные точки называют фокусами.

Каноническое уравнение эллипса:

X²/a² + y²/b² = 1, где a – большая полуось, b – меньшая полуось; х,у координаты точки М на эллипсе.

Точки пересечения эллипса с осями симметрии, называются вершинами эллипса.

Отношение c к большой полуоси эллипса, называется эксцентриситетом и обозначается:

= c/a (с – половина расстояния между фокусами)

При изучении эллипса особую роль играют две прямые, перпендикулярные к большой его оси и расположенные симметрично относительно центра на расстоянии а/ от него. Эти прямые называются директрисами эллипса. Уравнение директрис в выбранной системе имеет вид:

x = - a/ и x = a/ .

Теорема: отношение расстояния от любой точки эллипса до фокуса к расстоянию ее до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса: r/d= .

 

 

27. Гипербола.

Гиперболой называется такое множество точек на плоскости, что модуль разности расстояний от любой точки этого множества до двух данных точек плоскости есть величина постоянная, меньшая расстояния между данными точками и отличная от нуля. Данные точки называются фокусами.

Каноническое уравнение гиперболы:

X²/a² - y²/b² = 1

Точка пересечения осей симметрии гиперболы называется её центром. Точки пересечения оси симметрии Ox с гиперболой называются вершинами гиперболы. Число a называется действительной полуосью, b – мнимой.

Уравнению y²/b² - X²/a² = 1

Соответствует гипербола, фокусы которой расположены на оси Oy. Гипербола состоит из двух отдельных кривых, называемых её ветвями.

Ассимптотой кривой называется прямая, обладающая следующим свойством: расстояние от точки кривой до этой прямой стремится к нулю, когда точка удаляется от начала координат на бесконечность, двигаясь по этой кривой.

У гиперболы, заданной формулой X²/a² + y²/b² = 1, есть две асимптоты: y = +- (b/a) *x

У гиперболы y²/b² - X²/a² = 1 ассимптотами являются эти же две прямые.

Эксцентриситетом гиперболы называется отношение полуфокусного расстояния с к действительной оси. Они называются директрисами. Уравнения директрис имеет имеют следующий вид: x = +- a/ .

28. Парабола.

Параболой называется множество точек плоскости, каждая из которых равноудалена от принадлежащих этой плоскости данных прямой и точки, не лежащей на этой прямой. Данная точка называется фокусом, а данная прямая – директрисой. Расстояние от точки до директрисы обозначается р(р>0) – параметр параболы.

Каноническое уравнение параболы:

y² = 2px.

Когда р = ½, получаем уравнение y² = х. Это парабола, ветви которой направлены вправо.