
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная зависимость и линейная независимость векторов линейного пространстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим векторы Определение 4. Вектор Определение 5. Комбинация называется тривиальной, если все Определение 6.Система векторов называется линейно зависимой, если существует нетривиальная комбинация этих векторов, равная нулевому вектору. Если только тривиальная комбинация равна нулевому вектору, то система называется линейно независимой. Система, состоящая из одного ненулевого вектора x, линейно независима т. к. Пример 5. В линейном пространстве Для векторов линейного пространства справедливы следующие утверждения: 1. Если к системе n линейно зависимых векторов присоединить любые m векторов, то получим систему n + m линейно зависимых векторов. 2. Если в системе, содержащей n линейно независимых векторов, убрать любые m векторов (m ‹ n), то оставшиеся векторы образуют линейно независимую систему. 3. Если среди векторов 4. Если среди векторов Теорема. (Критерий линейной зависимости векторов). Для того, чтобы векторы
36. Размерность и базис линейного пространства. Координаты вектора линейного пространства.
Определение 7.Пусть в линейном пространстве V выполняются следующие условия: 1) существует n линейно независимых векторов; 2) любая система n + 1 векторов линейно зависима. Тогда число n называется размерностью пространства V. Если пространство состоит из одного элемента, то её размерность положим равной 0. Обозначается размерность Определение 8. Пространство V размерности n будем называть n-мерным пространством. Определение 9. Базисом n -мерного пространства называется любой упорядоченный набор из n линейно независимых векторов. Теорема. Если
Число
Теорема. Если Пример 6.В пространстве Пусть заданы два линейных пространства V и Определение 10.Два линейных вещественных пространства V и Теорема. Два линейных вещественных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность. Координаты вектора Теорема. Если
Группируя слагаемые, получим
Отсюда следует, что
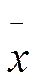 по базису по базису  . Это выражение можно записать в матричной форме . Это выражение можно записать в матричной форме  
Числа Если вектор Пример 7.Пусть V - пятимерное линейное пространство с базисом
Аналогично Справедливы следующие утверждения: 1. Вектор является нулевым вектором пространства тогда и только тогда, когда все его координаты в любом базисе равны нулю. 2. Координаты суммы двух векторов в некотором базисе равны сумме соответствующих координат этих векторов в том же базисе. 3. Координаты произведения вектора на число в некотором базисе равны произведению соответствующих координат данного вектора в том же базисе на это число. Два вектора равны между собой тогда и только тогда, когда равны между собой их соответствующие координаты в одном и том же базисе.
№ 37. Преобразование координат вектора при изменении базиса
Пусть в линейном пространстве V заданы два произвольных базиса Чтобы выразить векторы базиса Пусть
которые называются матрицами перехода от одного базиса к другому. Из соотношений и следует, что Пусть
Выясним, как преобразуются координаты вектора при переходе от одного базиса к другому. Подставим в выражение
Сравним полученное выражение с выражением. Коэффициенты при
Аналогично В матричной форме формулы и запишутся в виде
где
Евклидово пространство. Для того, чтобы в линейном пространстве можно было измерять длины и углы, вводят новую операцию – скалярное произведение. Пусть Аксиома 13.1. Скалярное произведение векторов коммутативно: Аксиома 13.2. Скалярное произведение векторов дистрибутивно относительно сложения векторов: Аксиома 13.3. Числовой множитель можно вынести за знак скалярного произведения: Аксиома 13.4 Скалярный квадрат вектора неотрицателен: Линейное пространство размерности n со скалярным произведением, удовлетворяющим аксиомам (13.1)-(13.4), называется n -мерным евклидовым пространством и обозначается Пример 3. 1. Евклидовым пространством является множество всех векторов 2. Евклидовым пространством является множество Т функций, непрерывных на отрезке 3. Если в арифметическом линейном пространстве Определение13. Величиной угла между двумя векторами
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |


 также принадлежит V и называется линейной комбинацией векторов
также принадлежит V и называется линейной комбинацией векторов  Числа
Числа  называются коэффициентами этой комбинации.
называются коэффициентами этой комбинации. ; если есть ненулевые коэффициенты, то она называется нетривиальной.
; если есть ненулевые коэффициенты, то она называется нетривиальной. возможно лишь при
возможно лишь при  . Система, состоящая из нулевого вектора
. Система, состоящая из нулевого вектора  , линейно зависима, т. к.
, линейно зависима, т. к.  даже при
даже при  .
.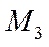 любые два коллинеарных вектора линейно зависимы. Пусть векторы х вектора линейно зависимо
любые два коллинеарных вектора линейно зависимы. Пусть векторы х вектора линейно зависимо 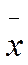 и
и  коллинеарны. Из этого следует, что существует такое число
коллинеарны. Из этого следует, что существует такое число  , что
, что 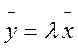 . Тогда
. Тогда  – нетривиальная комбинация, равная нулевому вектору.
– нетривиальная комбинация, равная нулевому вектору. имеются
имеются  и
и  такие, что
такие, что  , где
, где  – число, то векторы
– число, то векторы  линейно зависимы.
линейно зависимы. были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных. (от англ. dimension – размерность).
(от англ. dimension – размерность).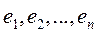 – базис n-мерного пространства V, то любой вектор
– базис n-мерного пространства V, то любой вектор  этого пространства линейно выражается через векторы
этого пространства линейно выражается через векторы  , т. е.
, т. е. .
. Пусть
Пусть  . Тогда система
. Тогда система  из n + 1 вектора линейно зависима, т. е.
из n + 1 вектора линейно зависима, т. е.  .
. , т. к. иначе получилась бы нетривиальная комбинация векторов
, т. к. иначе получилась бы нетривиальная комбинация векторов 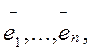 равная нулю. Выражаем вектор
равная нулю. Выражаем вектор  из этого уравнения:
из этого уравнения: , что и требовалось доказать.
, что и требовалось доказать. 
 – система линейно независимых векторов пространства V и любой вектор
– система линейно независимых векторов пространства V и любой вектор  этого пространства линейно выражается через
этого пространства линейно выражается через  , то пространство V является n-мерным.
, то пространство V является n-мерным. из примера 1 базис образуют три вектора
из примера 1 базис образуют три вектора  . Они линейно независимы, и каждый вектор линейно выражается через них. Следовательно, размерность пространства
. Они линейно независимы, и каждый вектор линейно выражается через них. Следовательно, размерность пространства 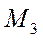 равна трём.
равна трём.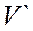 . Если между элементами этих пространств установлено взаимнооднозначное соответствие, причём
. Если между элементами этих пространств установлено взаимнооднозначное соответствие, причём  соответствует
соответствует  , то пишут
, то пишут  .
. называются изоморфными, если между их элементами можно установить взаимно-однозначное соответствие так, что если
называются изоморфными, если между их элементами можно установить взаимно-однозначное соответствие так, что если  ,
,  , то
, то 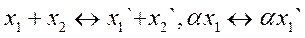 , где
, где  – вещественное число.
– вещественное число. – базис линейного пространства, то для любого вектора
– базис линейного пространства, то для любого вектора 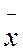 этого пространства существует единственная система чисел
этого пространства существует единственная система чисел  такая, что
такая, что  .
. Из теоремы 12.2 следует существование такой системы
Из теоремы 12.2 следует существование такой системы  , что выполняется. Докажем единственность. Допустим, что существует другая система
, что выполняется. Докажем единственность. Допустим, что существует другая система  , такая, что
, такая, что  . Тогда
. Тогда  .
. .
. , поскольку векторы
, поскольку векторы  линейно независимы. Теорема доказана.
линейно независимы. Теорема доказана. 
 называются координатами вектора
называются координатами вектора  в базисе
в базисе  .
. имеет в некотором базисе координаты
имеет в некотором базисе координаты  , то пишут
, то пишут  .
.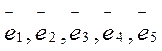 . Найти координаты векторов
. Найти координаты векторов  и
и  .
. , т.е.
, т.е.  имеет координаты (2,0,-1,3,0).
имеет координаты (2,0,-1,3,0). и
и  . Выразим векторы
. Выразим векторы  через
через  . Пусть
. Пусть  , где
, где  - координаты вектора
- координаты вектора  в базисе
в базисе  .
. через
через  , нужно решить систему уравнений относительно векторов
, нужно решить систему уравнений относительно векторов  . Эта система имеет единственное решение, поскольку её определитель отличен от нуля.
. Эта система имеет единственное решение, поскольку её определитель отличен от нуля.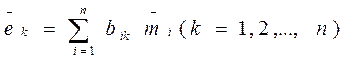 –
–  и
и  составим матрицы:
составим матрицы:
 .
. – произвольный вектор пространства V, который в базисе
– произвольный вектор пространства V, который в базисе  имеет координаты
имеет координаты 
 , а в базисе
, а в базисе  –
–  , т. е.
, т. е. ;
; .
. .
. должны быть равны
должны быть равны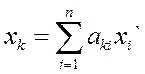

 ,
, ;
; 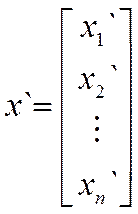 .
. –
–  и
и  ставится в соответствие действительное число
ставится в соответствие действительное число 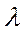 – их скалярное произведение, обозначаемое
– их скалярное произведение, обозначаемое  , удовлетворяющее следующим аксиомам.
, удовлетворяющее следующим аксиомам.
 .
. .
. , причём
, причём  тогда и только тогда, когда
тогда и только тогда, когда  .
.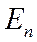 .
. обычного трёхмерного пространства. Скалярное произведение вводится так же, как в лекции 2, т. е. как произведение длин этих векторов на косинус угла между ними.
обычного трёхмерного пространства. Скалярное произведение вводится так же, как в лекции 2, т. е. как произведение длин этих векторов на косинус угла между ними. . Скалярное произведение функций f и φ определим так:
. Скалярное произведение функций f и φ определим так:  . Выполнение аксиом (13.1)-(13.4) непосредственно проверяется.
. Выполнение аксиом (13.1)-(13.4) непосредственно проверяется. скалярное произведение векторов
скалярное произведение векторов 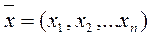 и
и  задать равенством
задать равенством  , то аксиомы (13.1)-(13.4) выполняются.
, то аксиомы (13.1)-(13.4) выполняются. и
и  называется угол
называется угол  такой, что
такой, что  , где
, где  норма вектора
норма вектора  .
.


