
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение линейного пространства и простейшие следствия из аксиом.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение линейного пространства и простейшие следствия из аксиом. Определение. Линейным (векторным) пространством над полем Р называется множество V элементов произвольной природы, в котором заданы две операции: внутренняя – сложение, и внешняя – умножение на числа из Р, причем эти операции удовлетворяют следующим аксиомам. 1*. 2*. 3*. 4*. 5*. 6*. 7*. 8*. Если P = R, то линейное пространство называется действительным, если Р = С, то комплексным. Простейшие следствия из аксиом. Линейное пространство впредь будем обозначать буквой V. 1º. В линейном пространстве существует единственный нейтральный элемент. ► Предположим, что в некотором линейном пространстве есть два нейтральных элемента:
Итак, мы пришли к противоречию.◄ 2º. В линейном пространстве, каждый элемент имеет единственный противоположный. ►Предположим, что некоторый элемент
опять пришли к противоречию.◄ 3º. ► Замечание. При доказательстве следствий можно использовать либо аксиомы, либо уже доказанные следствия. 4º. ► Таким образом, 5º. ► 6º. В линейном пространстве из равенства ►а) б)
Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости. Определение. Система элементов
линейного пространства
Система (3.1) называется линейно независимой, если равенство (3.2) выполняется только в том случае, когда
т. е. когда из равенства (3.2) вытекает (3.3).
Базис и координаты в линейном пространстве. Свойства координат векторов.
Определение.Базисом линейного пространства V над полем Р называется упорядоченная система
элементов этого пространства, удовлетворяющая следующим условиям: 1)
2) система (3.18) линейно независима. Если система (3.18) удовлетворяет только одному первому условию, то она называется системой образующих линейного пространства V. Таким образом, базис линейного пространства – это его линейно независимая система образующих. Числа
Свойства координат векторов
1º. Если все координаты вектора в некотором базисе равны нулю, то этот вектор – нулевой. ►Доказательство очевидным образом вытекает из аксиом линейного пространства и следствий к ним: 2º. Все координаты нулевого вектора в любом из базисов равны нулю. ►Пусть (
разложение нулевого вектора по базису (3.22). В силу линейной независимости (3.22) из (3.23) вытекает, что 3º. Координаты вектора в данном базисе определяются однозначно. ►Пусть некоторый вектор
= [аксиомы 1*, 2* и 6* из определения линейного пространства] = = Равенство (3.24) – это разложение по базису (3.22) нулевого вектора, и поэтому все коэффициенты разложения равны нулю, следовательно, 4º. При сложении векторов их соответствующие координаты складываются. ► Пусть заданы векторы
Равенство (3.25) – это разложение вектора 5º. При умножении вектора на число все его координаты умножаются на это число. Свойство доказывается точно так же, как и предыдущее, это вы можете сделать самостоятельно. Следствие. Координаты линейной комбинации векторов равны таким же (с такими же коэффициентами) линейным комбинациям соответствующих координат слагаемых, т. е. если
Свойства матрицы перехода 1º. Матрица перехода от одного базиса к другому определяется однозначно. ►Вытекает из того, что она состоит из координатных столбцов векторов одного базиса в другом.◄ 2º. Матрица перехода всегда невырождена. ►На основании матричного критерия линейной независимости.◄ 3º. Если Т – невырожденная квадратная матрица n -го порядка и
некоторый базис пространства
такой, что Т – матрица перехода от (3.46) к (3.47). ►Пусть 4º. Матрица перехода от базиса ►Доказательство вытекает из равенства 5º. Если Т – матрица перехода от базиса (3.46) к базису (3.47),а
то матрицей перехода от (3.46) к (3.48) является матрица ►Действительно, 6º. Если Т – матрица перехода от (3.46) к (3.47), то матрицей перехода от (3.47) к (3.46) является ►(3.45) Замечание. По аналогии с равенством (3.44) естественно записать равенство
Определение линейного пространства и простейшие следствия из аксиом. Определение. Линейным (векторным) пространством над полем Р называется множество V элементов произвольной природы, в котором заданы две операции: внутренняя – сложение, и внешняя – умножение на числа из Р, причем эти операции удовлетворяют следующим аксиомам. 1*. 2*. 3*. 4*. 5*. 6*. 7*. 8*. Если P = R, то линейное пространство называется действительным, если Р = С, то комплексным.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

 – коммутативность сложения.
– коммутативность сложения. – ассоциативность сложения.
– ассоциативность сложения. существование нейтрального элемента).
существование нейтрального элемента). – существование противоположного элемента.
– существование противоположного элемента. .
. .
. .
. .
. и
и  . Тогда
. Тогда
 имеет два различных противоположных:
имеет два различных противоположных:  и
и  , т. е.
, т. е.  . Получаем
. Получаем
 –
–





 ◄
◄


 – противоположный к
– противоположный к  . Поэтому на основании 2-го следствия
. Поэтому на основании 2-го следствия  ◄
◄
 ◄
◄ вытекает: либо
вытекает: либо  , либо
, либо  .
. Тогда имеем:
Тогда имеем: 

 ◄
◄ (3.1)
(3.1) над полем Р называется линейно зависимой, если существуют числа
над полем Р называется линейно зависимой, если существуют числа  из поля Р, не все равные 0, такие что
из поля Р, не все равные 0, такие что . (3.2)
. (3.2)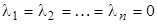 , (3.3)
, (3.3) (3.18)
(3.18) , такие, что
, такие, что (3.19)
(3.19) в равенстве (3.19) называются координатами вектора
в равенстве (3.19) называются координатами вектора  в базисе (3.18), а само равенство (3.19) – разложением вектора
в базисе (3.18), а само равенство (3.19) – разложением вектора  . ◄
. ◄ ) – (3.22) базис линейного пространства
) – (3.22) базис линейного пространства  (3.23)
(3.23) . ◄
. ◄ и
и  . Тогда
. Тогда
 (
(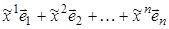 ) =
) =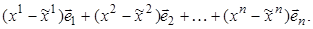 (3.24)
(3.24)
 , что противоречит условию. ◄
, что противоречит условию. ◄ своими координатами в базисе (3.22) и пусть
своими координатами в базисе (3.22) и пусть  Тогда
Тогда
 (3.25)
(3.25) по базису (3.22), следовательно, коэффициенты разложения – координаты вектора
по базису (3.22), следовательно, коэффициенты разложения – координаты вектора  ◄
◄ и
и 
 то
то
 , то в
, то в  (3.47)
(3.47) Положим
Положим  (т. е.
(т. е.  – вектор, чей координатный столбец в базисе (3.46) совпадает с i -м столбцом матрицы Т). Тогда (3.47) – линейно независимая система на основании матричного критерия, а значит, в
– вектор, чей координатный столбец в базисе (3.46) совпадает с i -м столбцом матрицы Т). Тогда (3.47) – линейно независимая система на основании матричного критерия, а значит, в  .◄
.◄ - матрица перехода от (3.47) к базису
- матрица перехода от (3.47) к базису , (3.48)
, (3.48)
 ,
,  , и поэтому
, и поэтому  . Утверждение вытекает из определения матрицы перехода.◄
. Утверждение вытекает из определения матрицы перехода.◄
 , и утверждение опять вытекает из определения матрицы перехода.◄
, и утверждение опять вытекает из определения матрицы перехода.◄ , и поэтому элементы матрицы перехода от (3.47) к (3.46) естественно обозначать
, и поэтому элементы матрицы перехода от (3.47) к (3.46) естественно обозначать  . Учитывая, что эта матрица есть не что иное, как
. Учитывая, что эта матрица есть не что иное, как  получаем:
получаем:  Так как
Так как  и
и  то
то  и
и 



