
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
N-мерный вектор и векторное пространство ⇐ ПредыдущаяСтр 3 из 3
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства. Определение. n-мерньм вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Понятие n-мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. х=у, если Суммой двух векторов одинаковой размерности n называется вектор z=х +у‚ компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. Произведением вектора х на действительное число λ называется вектор и u= λX компоненты u(итое(i)), которого равны произведению.
14. Векторное(линейное) пространство, его размерность и базис. Теорема о существовании и единственности разложения вектора линейного пространства по векторам базиса.
15. Скалярное произведение вектаров в n-мерном пространстве. Евклидово пространство.Длина(норма) вектора.
16. Ортогональные векторы. Ортогональный и ортонормированный базисы. Теорема о существовании ортонормированного базиса в евклидовом пространстве.
17.Определение оператора. Понятие линейного оператора. Образ и прообраз векторов.
18. Матрица линейного оператора в базисе, состоящем из его собственных векторов. Пример.
19. Собственные векторы и собственные значения оператора А(матрицы А). Характеристический многочлен оператора и его характеристическое уравнение.
20. Матрица линейного оператора в заданном базисе: связь между вектором x и образом y.Ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы.
21. Квадратичная форма(определение). Матрица квадратичной формы. Ранг квадратичной формы.Пример.
22. Квадратичная форма(канонический вид). Приведение квадратичной формы к каноническому виду. Пример. Закон инерции квадратических форм)
23. Положительно и отрицательно определённая,знакоопределённая квадратичные формы. Критерии знакоопределённости квардратичной формы(через собственные значения её матрицы и по критерию Сильвества).
24. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести). Опр. Урав-ем линии(кривой) на плоскости Oxy наз-ся урав-е, кот.удовлетворяют координаты x и y каждой точки данной линии и не удовлет.координаты любой точки, не лежащей на этой линии. Точка пересеч-я двух линий: система двух прямых A1x+B1y+C1=0;A2x+B2y+C2=0 – если прямые не параллельны, т.е. А1/А2 НЕ РАВНО В1/В2, то реш-е системы дает единственную точку пересеч-я прямых. Осн.виды урав-ий прямой на плос-ти: 1) Урав-е пря-й, проход-щей через данную точку в данном направ-и: y-y1=k(x-x1). 2) Если в урав-и k-производное число,то это урав-е определяет пучок прямых,проходящих через точку M1(x1, y1), кроме прямой, параллельной оси Oy и не имеющей углового коэффициента. При-р:урав-е пучка прямых, проходящ-х через точку A(3;-2), имеет вид y+2=k(x-3). 3) Урав-е прямой, проходящ-й через две данные точки: угловой коэф-т прямой:k=y2-y1/x2-x1. y-y1=y2-y1/x2-x1 * (x-x1). 4) Урав-е прямой в отрезках наз-ся урав-е x/a +y/b=1. 5) Общее урав-е прямой и его исследование: При любых А,В(не равных одновременно нулю) и С урав-е (Ах+By+C=0) есть урав-е некоторой прямой линии на плоскости Oxy. Ах+By+C=0 наз-ся общим урав-ем прямой.
25. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых.
26. Кривые второго порядка, их общее уравнение. Нормальное уравнение окружности.Каноническое уравнение эллипса.Геометрический смыслпараметров окружности и эллипса.
27. Канонические уравнения гиперволы и параболы,геометрический смысл их параметров.Уавнение асимптот гиперболы.График обратно пропорциональной зависимости и квадратного трёхчлена.
28. Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости. Условия параллельности и перпендикулярности двух плоскостей.
29. Уравнения прямой линии в пространстве как линии пересечения двух плоскостей. Канонические уравнения прямой. Направляющий вектор прямой. Условия параллельности и перпендикуляр Условие параллельности плоскостей ности двух прямых в пространстве.
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:
30. Угол между двумя плоскостями, между двумя прямыми, между прямой и плоскостью. Условие параллельности двух плоскостей, двух прямых, прямой и плоскости.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.127 (0.016 с.) |



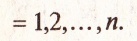












































 Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов .
. - условие параллельности прямых.
- условие параллельности прямых. – условие перпендикулярности прямых.
– условие перпендикулярности прямых.


