
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное пространство. Пространства арифметических и алгебраических векторов.Содержание книги
Поиск на нашем сайте
Векторное пространство. Пространства арифметических и алгебраических векторов. Вектор- элемент линейного пространства н-мерным арифметическим вектором называется упорядоченный набор из н-вещественных чисел Обозначается x = (x 1, x 2,..., x n); числа x 1, x 2, ..., xn называются компонентами арифметического вектора. Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых x = (x 1, x 2,..., x n), y = (y 1, y 2,..., y n) и любого числа α справедливо: x + y = (x 1+ y 1, x 2 + y 2,..., x n + yn); α x = (αx 1, αx 2,..., α x n). Достаточно умножить на это число каждый компонент 2)сложение суммой 2х векторов называется вектор, компоненты которого являются суммами соответствующих компонентам этих векторов 1)умножение для того чтобы умножить, Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn. Вектор θ = (0, 0,..., 0) называется нулевым вектором Rn, а вектор − x = (− x 1, − x 2,..., − x n) — противоположным вектором для вектора x в Rn.
Геометрический вектор - направленный отрезок 2 направленных отрезка называется равными если
свободный вектор — это множество равных между собой направленных отрезков
Сумма векторов:
Разность векторов: Формула вычитания векторов: Признак коллинеарности векторов:
Векторное пространство Перевод Векторное пространство математическое понятие, обобщающее понятие совокупности всех (свободных) Векторовобычного трёхмерного пространства. Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа (см. Векторное исчисление). В применении к любым векторам х, у, z и любым числам α, β эти правила удовлетворяют следующим условиям (условия А): 1) х + у = у + х (перестановочность сложения); 2)(х + у)+ z = x +(y + z) (ассоциативность сложения); 3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x; 4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0, 5) 1 · х = х, 6) α (βx)=(αβ) х (ассоциативность умножения); 7) (α + β) х = αх + βх (распределительное свойство относительно числового множителя); 8) α (х + у)= αх + αу (распределительное свойство относительно векторного множителя). Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А (условия 1—3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу). Выражение α1e1 + α2e2 + … + αnen (1) называется линейной комбинацией векторов e1, e2,..., en с коэффициентами α1, α2, ..., αn. Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов α1, α2,..., αn отличен от нуля. Векторы e1, e2,..., en называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e1, e2,..., en равна нулевому вектору) векторы e1, e2,..., en называется линейно независимыми. Векторы (свободные) трёхмерного пространства удовлетворяют следующему условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми). В. п. называется n-мepным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e1, e2,..., en, а любые n + 1 элементов линейно зависимы (обобщённое условие В). В. п. называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного В. п. образуют базис этого пространства. Если e1, e2,..., en — базис В. п., то любой вектор х этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов: x = α1e1 + α2e2 + ... + αnen. При этом числа α1, α2,..., αn называются координатами вектора х в данном базисе.
Длина вектора Понятие вектора Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Направление вектора (от начала к концу) на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначается символом Длиной ненулевого вектора
Сложение матриц
Пусть Из определения следует, что складывать можно только матрицы одинаковых размеров.
Умножение матрицы на число
Произведением матрицы
Произведение обозначается
Умножить на число можно любую матрицу, при этом каждый ее элемент умножается на это число.
5. Модели планирования производства. ???????? Системы линейных уравнений
Если все Уравнение прямой в отрезках
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1,
Нормальное уравнение прямой
Если обе части уравнения Ах + Ву + С = 0 разделить на число
xcosφ + ysinφ - p = 0 – нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ? С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой. уравнение этой прямой в отрезках: уравнение этой прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой:
C ледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см 2. Уравнение прямой имеет вид: a = -4 не подходит по условию задачи. Итого:
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Уравнение прямой имеет вид:
Коллинеарные прямые
Две прямые называются коллинеарными, если они параллельны или совпадают.
Получим условие коллинеарности двух прямых
и наоборот. Прямые совпадают, если помимо этих условий справедливо
Таким образом, прямые (3.19) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число
Условия параллельности или совпадения прямых (3.19) можно записать в виде
Условие коллинеарности двух прямых (3.19) можно записать в виде
Пересекающиеся прямые
Необходимым и достаточным условием пересечения двух прямых (3.19) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:
Угол между прямыми
Углом между двумя прямыми на плоскости называется угол между их направляющими векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до
Если
Чтобы получить величину
Угол
Чтобы получить величину
Необходимым и достаточным условием перпендикулярности прямых (3.19) является условие ортогональности их нормалей, т.е.
По формуле (3.22) получаем острый угол
Если прямые заданы уравнениями с угловыми коэффициентами:
Если правая часть (3.23) положительна, то угол
Если Плоскостями.) ??? Плоскость в пространстве План лекции 1. Уравнение плоскости. Полное и неполные уравнения плоскости. 2. Частные случаи уравнения плоскости. 3. Нормальное уравнение плоскости. Расстояние от точки до плоскости. 4. Взаимное расположение двух плоскостей в пространстве.
1. Уравнение плоскости. Полное и неполные уравнения плоскости. Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида:
Обратно, множество всех точек (1) – общее уравнение плоскости. Пусть точка Вычтем (2) из (1):
Следовательно, векторы Неполные уравнения плоскости: А) Б) В) Г) Д) Е) Ж) 2. Частные случаи уравнения плоскости. Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку
Прилагая векторы В координатной форме уравнение (3) записывается так:
(4) – параметрическое уравнение плоскости. Уравнение (4) выражают линейную зависимость столбцов матрицы
Что эквивалентно равенству:
Пример. Найти уравнение плоскости, проходящей через три данные точки: Решение. Искомая плоскость содержит точку
Если все коэффициенты уравнения (1) отличны от нуля, тогда его можно записать в виде:
Или
Где (6) – уравнение плоскости в отрезках, т.к. числа 3. Нормальное уравнение плоскости. Расстояние от точки до плоскости. Пусть дана плоскость Или
(7) – нормальное уравнение плоскости. Теорема. Расстояние
Доказательство. Спроектируем точку
Теорема доказана. Если плотность
4. Взаимное расположение двух плоскостей в пространстве. Пусть в пространстве даны две плоскости
Соответствующие им векторы нормали имеют вид
Плоскости в пространстве могут быть параллельны, совпадать, перпендикулярны и, наконец, пересекаться под произвольным углом. Рассмотрим эти случаи. А) Плоскости Б) Плоскости В) Плоскости пересекаются под прямым углом, тогда и Г) Плоскости пересекаются под произвольным углом; найдем этот угол. За угол между плоскостями принимается угол
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами
Пример. Определить угол между плоскостями x +2 y -3 z +4=0 и 2 x +3 y + z +8=0.
Эллипс.
Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная.
Замечание. При совпадении точек F 1 и F 2 эллипс превращается в окружность. Выведем уравнение эллипса, выбрав декартову систему у М(х,у) координат так, чтобы ось Ох совпала с прямой F 1 F 2, начало r1 r2 координат – с серединой отрезка F 1 F 2. Пусть длина этого отрезка равна 2 с, тогда в выбранной системе координат F1 O F2 x F 1(- c, 0), F 2(c, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F 1 и F 2 равна 2 а. Тогда r 1 + r 2 = 2 a, но поэтому
Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.
Свойства эллипса: 1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2 а и 2 b (2 a >2 b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью. 2) Весь эллипс содержится внутри прямоугольника 3) Эксцентриситет эллипса e < 1.
Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса. Эллипс- кривая второго порядка.
Гипербола. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная. | r1 - r2| = 2 a, откуда
Свойства гиперболы: 1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси. 2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями 3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот. 4) Эксцентриситет гиперболы e > 1. 5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы. Доказательство можно провести так же, как и для эллипса.
Парабола.
Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой. у Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина d M(x,y) перпендикуляра FD, опущенного из фокуса на директри- r су, а координатные оси располагались параллельно и перпендикулярно директрисе. Пусть длина отрезка FD D O F x равна р. Тогда из равенства r = d следует, что называемому каноническим уравнением параболы. Величина р называется параметром параболы.
Свойства параболы: 1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат. 2) Вся парабола расположена в правой полуплоскости плоскости Оху.
Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение: Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e <1), гиперболу (при e >1) или параболу (при е =1).
Квадратичные формы
Квадратичная форма переменных
Если переменные
Матрица
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если Главные миноры матрицы A называются главными минорами квадратичной формы. В пространстве В пространстве
Векторное пространство. Пространства арифметических и алгебраических векторов. Вектор- элемент линейного пространства н-мерным арифметическим вектором называется упорядоченный набор из н-вещественных чисел | ||
|
| Поделиться: |

 (правило треугольника) (рис. 1.22);
(правило треугольника) (рис. 1.22); (правило параллелограмма) (рис. 1.23);
(правило параллелограмма) (рис. 1.23); (правило многоугольника);
(правило многоугольника);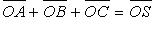 (правило параллелепипеда,
(правило параллелепипеда,  - диагональ).
- диагональ).
 (рис. 1.24).
(рис. 1.24).

 называется длина отрезка AB. Длина вектора
называется длина отрезка AB. Длина вектора  ) обозначается так:
) обозначается так: 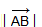
 . Длина нулевого вектора считается равной нулю:
. Длина нулевого вектора считается равной нулю:  .
. коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы
коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы  и
и 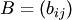 — матрицы одинаковых размеров
— матрицы одинаковых размеров  . Матрица
. Матрица  тех же размеров
тех же размеров  и
и  , если ее элементы равны сумме соответствующих элементов матриц
, если ее элементы равны сумме соответствующих элементов матриц 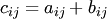

 . Сумма матриц обозначается
. Сумма матриц обозначается 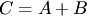 .
. называется матрица
называется матрица 
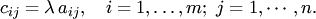
 или
или  .
.
 , i = 1, 2,..., m; j = 1, 2,..., n, - коэффициенты системы;
, i = 1, 2,..., m; j = 1, 2,..., n, - коэффициенты системы;  - свободные члены;
- свободные члены;  - переменные;
- переменные; 
 или
или , где
, где
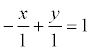 , а = -1, b = 1.
, а = -1, b = 1. , которое называется нормирующем множителем, то получим
, которое называется нормирующем множителем, то получим

 ; cos φ = 12/13; sin φ= -5/13; p = 5.
; cos φ = 12/13; sin φ= -5/13; p = 5. или х + у – 4 = 0.
или х + у – 4 = 0. >, где х 1 = у 1 = 0; x2 = -2; y2 = -3.
>, где х 1 = у 1 = 0; x2 = -2; y2 = -3.
 и
и  , заданных общими уравнениями:
, заданных общими уравнениями:
 и
и 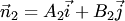 . Следовательно, если прямые (3.19) коллинеарны, то
. Следовательно, если прямые (3.19) коллинеарны, то  , т.е. существует такое число
, т.е. существует такое число  , что
, что . Тогда первое уравнение в (3.19) имеет вид
. Тогда первое уравнение в (3.19) имеет вид  , т.е. равносильно второму, поскольку
, т.е. равносильно второму, поскольку  , но
, но  . Прямые (3.19) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:
. Прямые (3.19) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:

 или
или 
 , которое определяет точку
, которое определяет точку  пересечения прямых (3.19).
пересечения прямых (3.19). . В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина
. В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина  угла между двумя прямыми удовлетворяет условию
угла между двумя прямыми удовлетворяет условию  .
.
 и
и  направляющие векторы прямых
направляющие векторы прямых  :
: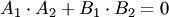
 (рис.3.23,а), и тупой в противном случае:
(рис.3.23,а), и тупой в противном случае:  (рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс
(рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс  или минус
или минус  соответственно.
соответственно.

 (условие параллельности прямых), то
(условие параллельности прямых), то  . Если
. Если  (условие перпендикулярности прямых), то правая часть (3.23) не определена
(условие перпендикулярности прямых), то правая часть (3.23) не определена  . Тогда полагают, что
. Тогда полагают, что  .
. (1)
(1) ,являющихся решениями произвольного уравнения (1), есть плоскость.
,являющихся решениями произвольного уравнения (1), есть плоскость. лежит в плоскости (1), тогда выполняется равенство:
лежит в плоскости (1), тогда выполняется равенство:  (2)
(2)
 и
и  ортогональны. Таким образом, вектор
ортогональны. Таким образом, вектор  является нормалью к плоскости (1) и называется нормальным вектором плоскости.
является нормалью к плоскости (1) и называется нормальным вектором плоскости. - уравнение плоскости, проходящей через начало координат;
- уравнение плоскости, проходящей через начало координат; - уравнение плоскости, параллельной оси
- уравнение плоскости, параллельной оси  ;
; - уравнение плоскости, параллельной оси
- уравнение плоскости, параллельной оси  ;
; - уравнение плоскости, параллельной оси
- уравнение плоскости, параллельной оси  ;
; - уравнение плоскости, параллельной координатной плоскости
- уравнение плоскости, параллельной координатной плоскости  ;
; - уравнение плоскости, параллельной координатной плоскости
- уравнение плоскости, параллельной координатной плоскости  ;
; - уравнение плоскости, параллельной координатной плоскости
- уравнение плоскости, параллельной координатной плоскости  .
. и
и  .
. и
и  к точке
к точке  , получим всевозможные закрепленные векторы вида
, получим всевозможные закрепленные векторы вида  , где
, где  - произвольные вещественные числа; концы
- произвольные вещественные числа; концы  этих векторов и заполняют плоскость, проходящую через точку
этих векторов и заполняют плоскость, проходящую через точку  .
. (4)
(4)
 (5)
(5) ;
;  .
. и
и  , следовательно, ее уравнение можно записать в виде (5):
, следовательно, ее уравнение можно записать в виде (5):

 (6)
(6) ;
;  ;
;  .
. - алгебраические значения отрезков, отсеченных плоскостью (1) на осях координат.
- алгебраические значения отрезков, отсеченных плоскостью (1) на осях координат.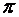 . Проведем через начало координат прямую
. Проведем через начало координат прямую  , будем называть эту прямую нормалью; точка
, будем называть эту прямую нормалью; точка  - пересечение плоскости
- пересечение плоскости  . Обозначим через
. Обозначим через  углы, которые составляет вектор
углы, которые составляет вектор  с осями координат;
с осями координат;  . Выведем уравнение плоскости
. Выведем уравнение плоскости  . Для этого возьмем на плоскости
. Для этого возьмем на плоскости  , отсяда
, отсяда 
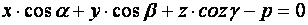 (7)
(7) от точки
от точки 
 на нормаль
на нормаль  - ее проекция, тогда
- ее проекция, тогда  или
или  , но
, но  ;
;  , следовательно,
, следовательно,

 и
и  :
:

 ,
, 
 , т.е.
, т.е.  .
. .
. , т.е.
, т.е.  .
. между любыми двумя перпендикулярными к ним векторами, следовательно, это будет угол между нормалями
между любыми двумя перпендикулярными к ним векторами, следовательно, это будет угол между нормалями  и
и  , а его можно вычислить по формуле:
, а его можно вычислить по формуле:
 Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
 и
и 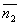 плоскостей α1 и α2 равен одному из указанных смежных двугранных углов
плоскостей α1 и α2 равен одному из указанных смежных двугранных углов  или
или  . Поэтому
. Поэтому  . Т.к.
. Т.к.  и
и  , то
, то .
.
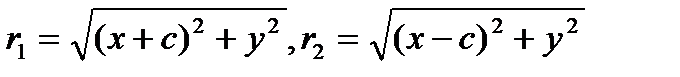 ,
, Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:
Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса: 




 Если обозначить b ² = c ² - a ², отсюда можно получить
Если обозначить b ² = c ² - a ², отсюда можно получить - каноническое уравнение гиперболы
- каноническое уравнение гиперболы и
и  .
. , (11.3`)
, (11.3`)

 поскольку
поскольку Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2 px
Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2 px - функция
- функция
 - коэффициенты квадратичной формы. Без ограничения общности считают
- коэффициенты квадратичной формы. Без ограничения общности считают  тогда
тогда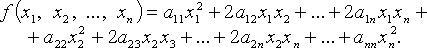
 квадратичная форма называется действительной.
квадратичная форма называется действительной.

 квадратичную форму можно записать в виде
квадратичную форму можно записать в виде  где X - координатный столбец вектора
где X - координатный столбец вектора 
 квадаратичную форму можно представить в виде
квадаратичную форму можно представить в виде 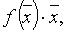 где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.


