
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие параллельности двух плоскостей.Содержание книги
Поиск на нашем сайте
Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
Условие перпендикулярности плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, Таким образом, Прямая в пространстве и ее различные уравнения. Угол между прямыми и между прямой и плоскостью. Точка пересечения прямой и плоскости.
угол между прямой и плоскостью 19. Геометрические объекты в пространстве Rn (прямая, луч, отрезок, гиперплоскость) Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений. Итак, если уравнения двух непараллельных плоскостей
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
Скалярное произведение в н-мерном пространстве. Определение, свойства, угол между векторами.
Эллипс. Вывод канонического уравнения. Эллипс.
Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная.
Замечание. При совпадении точек F 1 и F 2 эллипс превращается в окружность. Выведем уравнение эллипса, выбрав декартову систему у М(х,у) координат так, чтобы ось Ох совпала с прямой F 1 F 2, начало r1 r2 координат – с серединой отрезка F 1 F 2. Пусть длина этого отрезка равна 2 с, тогда в выбранной системе координат F1 O F2 x F 1(- c, 0), F 2(c, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F 1 и F 2 равна 2 а. Тогда r 1 + r 2 = 2 a, но поэтому
Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.
Свойства эллипса: 1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2 а и 2 b (2 a >2 b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью. 2) Весь эллипс содержится внутри прямоугольника 3) Эксцентриситет эллипса e < 1.
Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса. Эллипс- кривая второго порядка.
Гипербола. Вывод канонического уравнения. Гипербола. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная. | r1 - r2| = 2 a, откуда
Свойства гиперболы: 1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси. 2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями 3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот. 4) Эксцентриситет гиперболы e > 1. 5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.
Доказательство можно провести так же, как и для эллипса.
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.225.27 (0.01 с.) |

 и
и 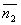 параллельны, а значит
параллельны, а значит  .
.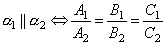 или
или 
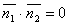 или
или 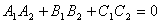 .
.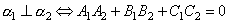 .
.
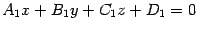 и
и , то прямая, являющаяся их линией пересечения, задается системой уравнений
, то прямая, являющаяся их линией пересечения, задается системой уравнений 


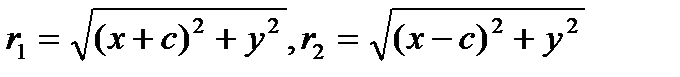 ,
, Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:
Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса: 
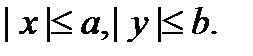




 Если обозначить b ² = c ² - a ², отсюда можно получить
Если обозначить b ² = c ² - a ², отсюда можно получить - каноническое уравнение гиперболы
- каноническое уравнение гиперболы и
и  .
. , (11.3`)
, (11.3`)




