
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейное (векторное) пространствоСодержание книги Поиск на нашем сайте
Как известно, линейные операции (сложение, вычитание, умножение на число) определены по-своему для каждого множества (числа, многочлены, направленные отрезки, матрицы). Сами операции различны, но их свойства одинаковы. Эта общность свойств позволяет обобщить понятие линейных операций для любых множеств вне зависимости от того, что это за множества (числа, матрицы и т.д.). Для того, чтобы дать определение линейного (векторного) пространства рассмотрим некоторое множество L действительных элементов, для которых определены операции сложения и умножения на число. Эти операции обладают свойствами: 1) Коммутативность + = + 2) Ассоциативность (+) + = + (+) 3)Существует такой нулевой вектор, что +=для L 4) Для L существует вектор = -, такой, что += 5)1 = 6) () = () 7) Распределительный закон ( + ) = + 8) (+) = +
Определение: Множество L, элементы которого обладают перечисленными выше свойствами, называется линейным (векторным) пространством, а его элементы называются векторами. Важно не путать понятие вектора, приведенное выше с понятием вектора как направленного отрезка на плоскости или в пространстве. Направленные отрезки являются всего лишь частным случаем элементов линейного (векторного) пространства. Линейное (векторное) пространство – понятие более широкое. Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д. Если операции сложения и умножения на число определены для действительных элементов, то линейное (векторное) пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.
2.1.1. Пространство арифметических векторов R n. Линейные операции с векторами Определение. Арифметическим вектором называется упорядоченная совокупность n чисел. Обозначается Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством рифметических векторов Rn. Вектор Для любых
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.
Линейная зависимость и независимость векторов. Базис. Говорят, что вектор Определение. Если хотя бы один вектор системы векторов Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой. Свойства базиса, естественный базис, координаты вектора в заданном базисе Итак установлено, что в пространстве Rn существует система из n линейно независимых векторов, а любые n +1 вектора линейно зависимы. Число n — размерность пространства Rn. Определение. Любая упорядоченная линейно независимая система n векторов Нетрудно показать, что любой вектор Числа Линейно независимая система векторов
образует базис в Rn, который называют естественным базисом в Rn.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.16.236 (0.008 с.) |

 , числа
, числа  называются компонентами арифметического вектора.
называются компонентами арифметического вектора. ,
, и
и  и любого числа
и любого числа 
 называется нулевым вектором, а вектор
называется нулевым вектором, а вектор 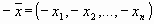 — противоположным вектором для вектора
— противоположным вектором для вектора  из Rn и любых чисел , справедливо:
из Rn и любых чисел , справедливо: , сложение коммутативно;
, сложение коммутативно; ,сложение ассоциативно;
,сложение ассоциативно;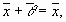
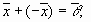
 , умножение на число ассоциативно;
, умножение на число ассоциативно;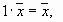 ;
; , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов; , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел. , если его можно представить в виде линейной комбинации этих элементов
, если его можно представить в виде линейной комбинации этих элементов  , т.е. представить в виде
, т.е. представить в виде  .
. из Rn линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
из Rn линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой. пространства арифметических векторов Rn называется базисом в Rn.
пространства арифметических векторов Rn называется базисом в Rn. единственным образом выражается через векторы базиса:
единственным образом выражается через векторы базиса:  . (На лекции единственность доказана).
. (На лекции единственность доказана). в базисе
в базисе 



