
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние от точки до прямойСодержание книги Поиск на нашем сайте
Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
Доказательство. Пусть точка М 1(х 1, у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x 0) + B(y – y0) + Ax0 + By0 + C = 0, то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
Теорема доказана.
Взаимное расположение прямых и исследование системы двух уравнений с двумя неизвестными. ??? 16 вопрос Коллинеарные прямые
Две прямые называются коллинеарными, если они параллельны или совпадают.
Получим условие коллинеарности двух прямых
и наоборот. Прямые совпадают, если помимо этих условий справедливо
Таким образом, прямые (3.19) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число
Условия параллельности или совпадения прямых (3.19) можно записать в виде
Условие коллинеарности двух прямых (3.19) можно записать в виде
Пересекающиеся прямые
Необходимым и достаточным условием пересечения двух прямых (3.19) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:
Угол между прямыми
Углом между двумя прямыми на плоскости называется угол между их направляющими векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до
Если
Чтобы получить величину
Угол
Чтобы получить величину
Необходимым и достаточным условием перпендикулярности прямых (3.19) является условие ортогональности их нормалей, т.е.
По формуле (3.22) получаем острый угол
Если прямые заданы уравнениями с угловыми коэффициентами:
Если правая часть (3.23) положительна, то угол
Если Плоскость в пространстве. (Различные виды уравнений плоскости, угол между Плоскостями.) ??? Плоскость в пространстве План лекции 1. Уравнение плоскости. Полное и неполные уравнения плоскости. 2. Частные случаи уравнения плоскости. 3. Нормальное уравнение плоскости. Расстояние от точки до плоскости. 4. Взаимное расположение двух плоскостей в пространстве.
1. Уравнение плоскости. Полное и неполные уравнения плоскости. Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида:
Обратно, множество всех точек (1) – общее уравнение плоскости. Пусть точка Вычтем (2) из (1):
Следовательно, векторы Неполные уравнения плоскости: А) Б) В) Г) Д) Е) Ж) 2. Частные случаи уравнения плоскости. Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку
Прилагая векторы В координатной форме уравнение (3) записывается так:
(4) – параметрическое уравнение плоскости. Уравнение (4) выражают линейную зависимость столбцов матрицы
Что эквивалентно равенству:
Пример. Найти уравнение плоскости, проходящей через три данные точки: Решение. Искомая плоскость содержит точку
Если все коэффициенты уравнения (1) отличны от нуля, тогда его можно записать в виде:
Или
Где (6) – уравнение плоскости в отрезках, т.к. числа 3. Нормальное уравнение плоскости. Расстояние от точки до плоскости. Пусть дана плоскость Или
(7) – нормальное уравнение плоскости. Теорема. Расстояние
Доказательство. Спроектируем точку
Теорема доказана. Если плотность
4. Взаимное расположение двух плоскостей в пространстве. Пусть в пространстве даны две плоскости
Соответствующие им векторы нормали имеют вид
Плоскости в пространстве могут быть параллельны, совпадать, перпендикулярны и, наконец, пересекаться под произвольным углом. Рассмотрим эти случаи. А) Плоскости Б) Плоскости В) Плоскости пересекаются под прямым углом, тогда и Г) Плоскости пересекаются под произвольным углом; найдем этот угол. За угол между плоскостями принимается угол
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами
Пример. Определить угол между плоскостями x +2 y -3 z +4=0 и 2 x +3 y + z +8=0.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.007 с.) |

 .
. (1)
(1)

 и
и  , заданных общими уравнениями:
, заданных общими уравнениями:
 и
и 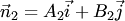 . Следовательно, если прямые (3.19) коллинеарны, то
. Следовательно, если прямые (3.19) коллинеарны, то  , т.е. существует такое число
, т.е. существует такое число  , что
, что . Тогда первое уравнение в (3.19) имеет вид
. Тогда первое уравнение в (3.19) имеет вид  , т.е. равносильно второму, поскольку
, т.е. равносильно второму, поскольку  , но
, но  . Прямые (3.19) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:
. Прямые (3.19) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:

 или
или 
 , которое определяет точку
, которое определяет точку  пересечения прямых (3.19).
пересечения прямых (3.19). . В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина
. В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина  угла между двумя прямыми удовлетворяет условию
угла между двумя прямыми удовлетворяет условию  .
.
 и
и  направляющие векторы прямых
направляющие векторы прямых  :
: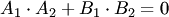
 (рис.3.23,а), и тупой в противном случае:
(рис.3.23,а), и тупой в противном случае:  (рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс
(рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс  или минус
или минус  соответственно.
соответственно.

 (условие параллельности прямых), то
(условие параллельности прямых), то  . Если
. Если  (условие перпендикулярности прямых), то правая часть (3.23) не определена
(условие перпендикулярности прямых), то правая часть (3.23) не определена  . Тогда полагают, что
. Тогда полагают, что  .
. (1)
(1) ,являющихся решениями произвольного уравнения (1), есть плоскость.
,являющихся решениями произвольного уравнения (1), есть плоскость. лежит в плоскости (1), тогда выполняется равенство:
лежит в плоскости (1), тогда выполняется равенство:  (2)
(2)
 и
и  ортогональны. Таким образом, вектор
ортогональны. Таким образом, вектор  является нормалью к плоскости (1) и называется нормальным вектором плоскости.
является нормалью к плоскости (1) и называется нормальным вектором плоскости. - уравнение плоскости, проходящей через начало координат;
- уравнение плоскости, проходящей через начало координат; - уравнение плоскости, параллельной оси
- уравнение плоскости, параллельной оси  ;
; - уравнение плоскости, параллельной оси
- уравнение плоскости, параллельной оси  ;
; - уравнение плоскости, параллельной оси
- уравнение плоскости, параллельной оси  ;
; - уравнение плоскости, параллельной координатной плоскости
- уравнение плоскости, параллельной координатной плоскости  ;
; - уравнение плоскости, параллельной координатной плоскости
- уравнение плоскости, параллельной координатной плоскости  ;
; - уравнение плоскости, параллельной координатной плоскости
- уравнение плоскости, параллельной координатной плоскости  .
. и
и  .
. и
и  к точке
к точке  , получим всевозможные закрепленные векторы вида
, получим всевозможные закрепленные векторы вида  , где
, где  - произвольные вещественные числа; концы
- произвольные вещественные числа; концы  этих векторов и заполняют плоскость, проходящую через точку
этих векторов и заполняют плоскость, проходящую через точку  .
. (4)
(4)
 (5)
(5) ;
;  .
. и
и  , следовательно, ее уравнение можно записать в виде (5):
, следовательно, ее уравнение можно записать в виде (5):

 (6)
(6) ;
;  ;
;  .
. - алгебраические значения отрезков, отсеченных плоскостью (1) на осях координат.
- алгебраические значения отрезков, отсеченных плоскостью (1) на осях координат.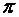 . Проведем через начало координат прямую
. Проведем через начало координат прямую  , будем называть эту прямую нормалью; точка
, будем называть эту прямую нормалью; точка  - пересечение плоскости
- пересечение плоскости  . Обозначим через
. Обозначим через  углы, которые составляет вектор
углы, которые составляет вектор  с осями координат;
с осями координат;  . Выведем уравнение плоскости
. Выведем уравнение плоскости  . Для этого возьмем на плоскости
. Для этого возьмем на плоскости  , отсяда
, отсяда 
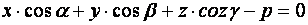 (7)
(7) от точки
от точки 
 на нормаль
на нормаль  - ее проекция, тогда
- ее проекция, тогда  или
или  , но
, но  ;
;  , следовательно,
, следовательно,

 и
и  :
:

 ,
, 
 , т.е.
, т.е.  .
. .
. , т.е.
, т.е.  .
. между любыми двумя перпендикулярными к ним векторами, следовательно, это будет угол между нормалями
между любыми двумя перпендикулярными к ним векторами, следовательно, это будет угол между нормалями  и
и  , а его можно вычислить по формуле:
, а его можно вычислить по формуле:
 Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
 и
и 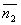 плоскостей α1 и α2 равен одному из указанных смежных двугранных углов
плоскостей α1 и α2 равен одному из указанных смежных двугранных углов  или
или  . Поэтому
. Поэтому  . Т.к.
. Т.к.  и
и  , то
, то .
.



