
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы координат в пространстве: декартовыСодержание книги Поиск на нашем сайте
Полярная система Полярная система координат задаётся т.О,наз.полюсом,лучом Ор,наз.полярной осью,и единичным вектором
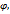 образованным отрезком ОМ с полярной осью и отсчитываемым в положительном направлении. образованным отрезком ОМ с полярной осью и отсчитываемым в положительном направлении.
 наз.полярными координатами т.М: r наз.полярным радиусом, наз.полярными координатами т.М: r наз.полярным радиусом, 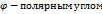
Системы координат в пространстве: декартовы Декартова система координат в пространстве определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1). Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной. 2)Общее ур.прямой: Ax +By+C=0 (A,B.C-постоянные коэффициенты,причём Аи В одновреммено не обращаются в 0 Ур.прямой с угловым коэффициентом имеет вид у=kx+b(k-угловой коэф.прямой,b-ордината точки пересечения прямой с осью Оу) Нормальное ур.прямой 3)Под углом между прямыми в плоскости понимают наименьший из двух смежных углов,образованными этими прямыми Если прямые Tg Условие параллельности прямых
Если прямые Для нахождения общих точек прямых
4)Расстоянием d от точки Расст.d опред.по фор.d= Расст.от точки d= Кривые второго порядка Линии,определяемые алгебраическими ур.второй степени относительно переменных х и у,т.е ур.вида А
Окружностью наз.множество всех точек плоскости,удалённых от заданной т.А на одно и тоже расстояние R. т.А наз.центром,а R-радиусом окружности Ур.окружности имеет вид Эллипсом наз.множество всех точек плоскости,сумма расст. от каждой из кот. до двух данных точек,наз.фокусами,есть величина постоянная,большая,чем расст. между фокусами Каноническое ур.эллипса: Точки А,В,С наз. вершинами эллипса,т.О-центром эллипса,расстояние Эксцентриситетом Фокальные радиусы опред.формулами Директрисами эллипса наз. 1)Если а=b,то ур. 2)ур.эллипса с осями,параллельными координатным,имеет вид 3)ур. Гиперболой наз.множество всех точек плоскости,модуль разности расстояний от каждой из которых до двух заданных точек,наз.фокусами,есть величина постоянная,меньшая,чем расстояние между фокусами Каноническое ур.гиперболы: Точки Аи В наз.вершинами гиперболы,т.О-центром гиперболы,расстояния Число Прямоугольник,центр которого совпадает с т.О,а стороны равны и параллельны осям гиперболы наз.основным прямоугольником гиперболы.Диагонали основного прямоугольника гиперболы лежат на двух прямых,наз.асимптотами гиперболы,они определяются ур.у= Две прямые Параболой наз.множество всех точек плоскости,каждая из которых равноудалена от заданной точки,наз.фокусом и заданной прямой,наз.директрисой Каноническое ур.параболы имеет вид
Ур.директрисы l параболы имеет вид х=-
6)Сложение векторов. Так как векторы - это направленные отрезки, то их сложение может быть выполнено геометрически. (Алгебраическое сложение векторов изложено ниже, в пункте «Единичные ортогональные векторы»). Предположим, что a = AB and b = CD, тогда вектор a + b = AB + CD есть результат выполнения двух операций a) параллельного переноса одного из векторов таким образом, чтобы его начальная точка совпала с конечной точкой второго вектора; б) геометрического сложения, т.е. построения результирующего вектора, идущего от начальной точки неподвижного вектора к конечной точке перенесённого вектора. Законы сложения. I. a + b = b + a (П е р е м е с т и т е л ь н ы й закон). II. (a + b) + c = a + (b + c) (С о ч е т а т е л ь н ы й закон). III. a + 0 = a. IV. a + (– a) = 0. 7)Скалярным произведением двух ненулевых векторов
Свойства скалярного произведения: 1. 2. 3. 4.
8) Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектор а, то его проекция обозначается аx. При проектировании этого же вектора на другую ось, скажем, ось Y, его проекция будет обозначаться аy (рис. 9).
Рис. 9 Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть аx = хк − xн. Надо помнить: проекция вектора на ось - это число! Причем, проекция может быть положительной, если величина хк больше величины хн, отрицательной, если величина хк меньше величины хн и равной нулю, если хк равно хн (рис. 10).
Рис. 10 Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Рис. 11 Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против. Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.
10.) Линейным пространством пространство 1. сложения, то есть каждой паре элементов множества
2. умножения на скаляр (то есть элемент поля При этом на операции накладываются следующие условия: 1. 2. 3. существует такой элемент 4. для любого 5. 6. 7. 8. Элементы множества
Система векторов e1,e2,..., ek линейного пространства L наз. линейно независимой системой, если равенство С1·e1+С2·e2+...+Сk· ek = 0 возможно только когда все коэффициенты С1, С2,..., Сk равны нулю. Здесь 0 — нулевой вектор линейного пространства L, С1, С2,..., Сk — числовые коэффициенты. Если система векторов e1,e2,..., ek линейного пространства L не явл. линейно независимой системой, то она наз. линейно зависимой системой векторов. Если векторы Рис.11.6.Угол между плоскостями Если через точку
Рис.11.8.Угол между нормальными векторами тупой
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула позволяет найти косинус острого угла между плоскостями. Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей: Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
16)Ур/ прямой в пространстве, проходящей через две точки A(x0,y0,z0) и B(x1,y1,z1)наз. равенство:
Угол между двумя прямыми равен углу между их направляющими векторами. Если прямые заданы след. урав:A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0 тогда направляющие векторы этих прямых будут равны: a1 = (- B1; A1) и a2 = (- B2; A2) Воспользуемся формулой скалярного произведения двух векторов:
из этой формулы получим:
Выразим угол φ:
Из последней формулы получим:
Если прямые параллельны, то k1=k2 и b1≠b2 Если прямые перпендикулярны, то k1*k2=-1 Если прямые пересекаются, то k1≠k2 Если прямые совпадают, то k1=k2 и b1=b2
Матрицы Матрицей А размера m на n наз.прямоугольная таблица из m строк и n столбцов,состоящая из чисел или иных матем.выражений Операции над матрицами Суммой матриц А= Произведение матриц А= Свойства операции умножения1)(A B)C=A(BC)=ABC 2)(A+B)C=AC+BC 3)A(B+C)=AC+BC 4)AB Транспонированной к матрице А= Диагональная матр., у кот. все элементы на главной диагонали равны 1, наз. единичной матрицей (Е).
Определители Определитель 2-го порядка задаётся равенством: Определитель 3-го порядка задаётся равенством: Определитель3-го порядка есть сумма 6=3! Слагаемых,каждое из которых представляет собой произведение 3-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одна половина слагаемых берётся со знаком +,другая со знаком -. 19)Алгеброическим дополнением Определитель n-го порядка задаётся равенством:
Сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одна половина слагаемых берется со знаком +,другая мо знаком -. 20)Обратной матрицей к квадратной матрице А наз.такая матрица,что
Если квадратеая матрица А-невырожденная,то Алгоритм нахождения:1)Вычислим определитель матрицы А,если опр.=0,то обратная матрица не сущ.2)Если опред.не равен 0,то обратная матрица сущ.Находим алгеброическое дополнение 21) Пусть K - поле, 22)Системы линейных уравнений. Система m линейных алгебраических уравнений с n неизвестными в линейной алгебре — это система уравнений вида
Здесь m — колич. Урав., а n — колич. неизвестных. Система линейных урав. может быть представлена в матричной форме как: Правило Крамера.Если определитель матрицы А отличен от 0, то система имеет единственное решение определяемое из форм.Xi=
ОДНОСТОРОННИЙ ПРЕДЕЛ
по проколотой окрестности точки х 0 (в этом случае его наз. также двусторонним, в отличие от односторонних пределов) существует тогда и только тогда, когда в точке х 0 существуют пределы слева и справа и они равны между собой. Обратная Пустьf(x)-- функ, непрерывная на отрезке [a,b].Предположим, что f(x) монотонна на [a,b]; пусть, для определённости, она монотонно возрастает: из x1<x2, следует, что f (x1)< f (x2) Тогда образом отрезка [a,b] будет отрезок [c,d], где c=f(a), d=f(b)(действительно, непрерывная функ. принимает любое промежуточное между f(a), f (b)значение, причём ровно один раз, что следует из монотонности). Поэтому сущ. обратная к y =f(x) функ. Теорема. Пусть f -- непрерывная монотонная функция, 36) Теорема 3 (теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном множестве функ. достигает на нем своего наибольшего и наименьшего значений. Непрерывность функ. на отрезке Функ. f (x) наз. непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала. Функ. f (x) наз. непрерывной на отрезке [ a, b ], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b. Замечание. Функ., непрерывная на отрезке [ a, b ] может быть разрывной в точках a и b (рис. 1)
Множество функ., непрерывных на отрезке [ a, b ] обозначается символом C [ a, b ]. Свойства функ., непрерывных на отрезке Теорема 1 (об ограниченности непрерывной функции). Если функ. f (x) непрерывна на отрезке [ a, b ], то она ограничена на этом отрезке, т.е. существует такое число C > 0, что " x О[ a, b ] выполняется неравенство | f (x)| ≤ C. Теорема 2 (Вейерштрасс). Если функ. f (x) непрерывна на отрезке [ a, b ], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. сущ. точки α, β О [ a, b ] такие, что m = f (α) ≤ f (x) ≤ f (β) = M для всех x О [ a, b ] (рис.2).
Наибольшее значение M обозначается символом max x О [ a, b ] f (x), а наименьшее значение m — символом min x О [ a, b ] f (x). Теорема 3 (о существовании нуля). Если функ. f (x) непрерывна на отрезке [ a, b ] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f (ξ) = 0. Геометрический смысл теоремы состоит в том, что график функ., удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).
Теорема 4 (Больцано–Коши). Если функция f (x) непрерывна на отрезке [ a, b ], то она принимает на (a, b) все промежуточные значения между f (a) и f (b). Существование непрерывной обратной функции Пусть функ. y = f (x) определена, строго монотонна и непрерывна на отрезке [ a, b ]. Тогда на отрезке [ α, β ] (α = f (a), β = f (b)) существует обратная функция x = g (y), также строго монотонная и непрерывная на отрезке (α, β). Определение Производной Производной ф-ции y=f(x) в тч. Х0 наз. предел отношения приращения этой ф-ции к приращению аргумента, когда последнее стремится к нулю. если он сущ. Формула Пусть f(x) определена на некотором промежутке (a, b). Тогда Уравнение касательной к кривой: Уравнение нормали к кривой: экономический смысл производной. Пусть y(x) – ф-ция, характеризующая, напр., издержки производства, где x – колич. выпускаемой продукции. Тогда отношение 38)Правила дифференцирования: Обозначим f(x) = u, g(x) = v - функ., дифференцируемые в точке х. 1. Производная сум.(разности) двух дифференц-ых ф-ций =сумме(разности) производных этих ф-ций Производная сложной функции и обратной функций Производная сложной ф.: Если Производная обратной ф.: Если y=f(x) и Дифференциал функции. Пусть функция y = f(x) имеет конечную производную в точке х:
Теорема Ферма и Ролля. Ферма: Пусть y=f(x) дифференцируется на некотором множестве X. Пусть некоторая точка этого множества в некоторой точке этого множества функ. достигает своего наибольшего или наименьшего значения, тогда производная в этой точке = 0. Ролля: Теорема Ро́лля утверждает, что если функ., имеющая производную на интервале, принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала. Пусть 1)y=f(x) определена и непрерывна на интервале 2)”y” дифференцируема по крайней мере на 3)в концах отрезка f принимает одинаковое значение f(a)=f(b). Тогда сущ. по крайней мере одна внутренняя точка, где производная =0. Теорема Лагранжа. 1.y=f(x) определена и непрерывна на 2.y=f(x) дифференцируема по крайней мере на (a,b). Тогда сущ. по крайней мере одна точка z где производная равна
43) Правило Лопиталя. Пусть функ. f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть
Коротко правило Лопиталя можно сф ормулировать след. образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных. Теорема Лагранжа
Если функ. f(x) непрерывна на замкнутом отрезке [a, b], дифференцируема внутри него, то сущ.такая точка с Î (a, b), что выполняется равенство Условия постоянства функции Условия монотонность функции: Монотонно возврастающая функ. если: f(
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.125 (0.015 с.) |

 того же направления,что и луч Ор.
того же направления,что и луч Ор. )
)
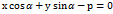 (р-длина перпендикуляра,опущ. из начала координат на прямую,
(р-длина перпендикуляра,опущ. из начала координат на прямую, 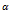 -угол,кот. этот перпендикуляр образует с полож. направлением оси Ох
-угол,кот. этот перпендикуляр образует с полож. направлением оси Ох заданы урав.с угловыми коэф. У=
заданы урав.с угловыми коэф. У= 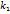 x+
x+  и у=
и у= 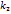 x+
x+  то угол
то угол 
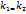 , а условие их перпедикулярности
, а условие их перпедикулярности 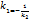
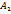 x+
x+  y+
y+  и
и 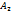 x+
x+ 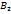 y+
y+ 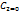 ,то величина
,то величина 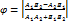
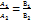
 димо решить систему ур.
димо решить систему ур.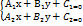
 ) до прямой
) до прямой  x+
x+ 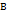 y+
y+  наз.длина перпендикуляра,опущенного из этой точки на прямую
наз.длина перпендикуляра,опущенного из этой точки на прямую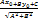
 до прямой
до прямой  выч. по форм.
выч. по форм.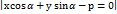
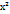 +2 Вху+С
+2 Вху+С 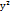 +2Dx+2Ey+F=0,наз.кривыми второго порядка
+2Dx+2Ey+F=0,наз.кривыми второго порядка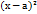 +
+  =
= 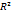 (каноническое урав.окружности).Если а=0,b=0,то ур.имеет вид
(каноническое урав.окружности).Если а=0,b=0,то ур.имеет вид 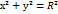
 =1,где а-большая полуось,b-малая полуось эллипса
=1,где а-большая полуось,b-малая полуось эллипса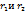 от произвольной точки М эллипса до его фокусов наз.фокальными радиусами этой точки
от произвольной точки М эллипса до его фокусов наз.фокальными радиусами этой точки эллипса наз.отношение фокусного расстояния 2с к большой оси 2а:
эллипса наз.отношение фокусного расстояния 2с к большой оси 2а: 
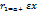 ,
, 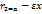
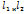 параллельные малой оси эллипса и отстоящие от неё на расстоянии,равном
параллельные малой оси эллипса и отстоящие от неё на расстоянии,равном  ,ур.директрис:x=
,ур.директрис:x= 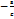
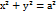
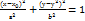
 t
t 
 ,наз.эксцентриситетом гиперболы
,наз.эксцентриситетом гиперболы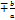 x
x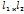 параллельные мнимой оси гиперболы и отстоящие от неё на расстоянии,равном
параллельные мнимой оси гиперболы и отстоящие от неё на расстоянии,равном  )Точка О(0,0)наз. Вершиной параболы,длина r отрезка FM-фокальный радиус т.М,ось Ох-ось симметрии параболы
)Точка О(0,0)наз. Вершиной параболы,длина r отрезка FM-фокальный радиус т.М,ось Ох-ось симметрии параболы ,фокальный радиус выч.по фор.r=x+
,фокальный радиус выч.по фор.r=x+ 
 наз.число, равное произведению длин этих векторов на косинус угла
наз.число, равное произведению длин этих векторов на косинус угла 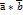 =
=  *
* 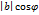
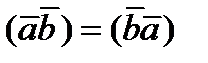 – переместительное свойство;
– переместительное свойство;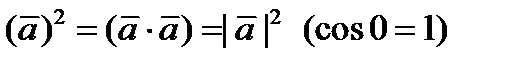 – скалярный квадрат вектора;
– скалярный квадрат вектора;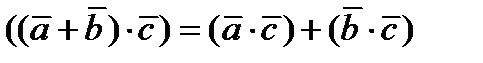 – распределительное свойство;
– распределительное свойство; – сочетательное свойство относительно числового множителя.
– сочетательное свойство относительно числового множителя.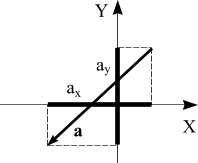
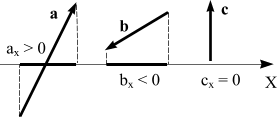

 над полем
над полем  — это непустое множество
— это непустое множество  , на котором введены операции
, на котором введены операции ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый  и
и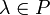 и любому элементу
и любому элементу  ставится в соответствие единственный элемент из
ставится в соответствие единственный элемент из 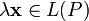 .
. , для любых
, для любых 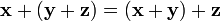 , для любых
, для любых 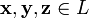 (ассоциативность сложения);
(ассоциативность сложения);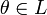 , что
, что 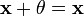 для любого
для любого  , что
, что 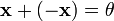 (существование противоположного элемента относительно сложения).
(существование противоположного элемента относительно сложения).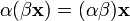 (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр); (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
(унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).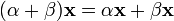 (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров);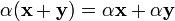 (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов). скалярное произведение кот. равно 0,наз.ортогональными
скалярное произведение кот. равно 0,наз.ортогональными провести плоскость
провести плоскость  , перпендикулярную линии пересечения плоскостей П1 и П2, то прямые l1 и l2 и изображения векторов n1 и n2 будут лежать в этой плоскости. Сделаем чертеж в плоскости
, перпендикулярную линии пересечения плоскостей П1 и П2, то прямые l1 и l2 и изображения векторов n1 и n2 будут лежать в этой плоскости. Сделаем чертеж в плоскости  Рис.11.7.Угол между нормальными векторами острый
Рис.11.7.Угол между нормальными векторами острый В одном варианте (рис. 11.7)
В одном варианте (рис. 11.7)  и
и  , следовательно, угол
, следовательно, угол  между нормальными векторами равен углу
между нормальными векторами равен углу  , являющемуся линейным углом острого двугранного угла между плоскостями П1 и.Во втором варианте (рис. 11.8)
, являющемуся линейным углом острого двугранного угла между плоскостями П1 и.Во втором варианте (рис. 11.8)  , а угол
, а угол  . Так как
. Так как  то в обоих случаях
то в обоих случаях  .По определению скалярного произведения
.По определению скалярного произведения  . Откуда
. Откуда 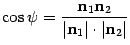 и соответственно
и соответственно 

 где
где  -- любое число.
-- любое число.




 .Квадратной матрицей n-го порядка наз.матрица размера n на n.Диагональной наз.квадратная матрица,у котрой все элементы вне главной диагонали равны 0.Единичной наз.диагональная матрица с единицами на главной диагонали.Нулевой наз.матрица,все элементы которой равны 0.
.Квадратной матрицей n-го порядка наз.матрица размера n на n.Диагональной наз.квадратная матрица,у котрой все элементы вне главной диагонали равны 0.Единичной наз.диагональная матрица с единицами на главной диагонали.Нулевой наз.матрица,все элементы которой равны 0. и B=
и B= 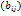 одинакового размера наз.матрица С=
одинакового размера наз.матрица С=  того же размера.Свойства операции сложения матриц.Для любых матриц А,B,C одного размера выполняются равенства:1)A+B=B+A 2)(A+B)+C=A+(B+C)=A+B+C
того же размера.Свойства операции сложения матриц.Для любых матриц А,B,C одного размера выполняются равенства:1)A+B=B+A 2)(A+B)+C=A+(B+C)=A+B+C
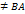
 =(
=( ) такая,что
) такая,что  .Элемент строки матрицы назовём крайним,если он отличён от 0,а все элементы этой строки,находящиеся левее него,равны 0.Матрица наз.ступенчатой,если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки
.Элемент строки матрицы назовём крайним,если он отличён от 0,а все элементы этой строки,находящиеся левее него,равны 0.Матрица наз.ступенчатой,если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки ).Опредилитель 2-го порядка есть сумма 2=2!слагаемых,каждое из кот. представляет собой произведение 2-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одно из слогаемых берется со знаком +,другое-со знаком -.
).Опредилитель 2-го порядка есть сумма 2=2!слагаемых,каждое из кот. представляет собой произведение 2-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одно из слогаемых берется со знаком +,другое-со знаком -.
 к элементу
к элементу  квадратной матрицы А=
квадратной матрицы А=  наз.произведение
наз.произведение  *
* 
 =
=  .Указанная сумма состоит из n!слагаемых,каждое из которых представляет собой произведение
.Указанная сумма состоит из n!слагаемых,каждое из которых представляет собой произведение
 *А=А*
*А=А*  =
=  ,получ.транспонированием из матрицы,составленной из алгебраических дополнений
,получ.транспонированием из матрицы,составленной из алгебраических дополнений 
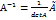 .
. элементов матрицы А и составляем матрицу из них
элементов матрицы А и составляем матрицу из них  3)Транспонируем матрицу
3)Транспонируем матрицу  4)Находим обратную матрицу по формуле
4)Находим обратную матрицу по формуле  5)Осущ.проверку А*
5)Осущ.проверку А* 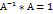
 ,
, 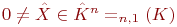 ,
,  . Если
. Если  , то
, то  называется собственным числом матрицы A, а
называется собственным числом матрицы A, а  - собственным вектором матрицы A, отвечающим собственному числу
- собственным вектором матрицы A, отвечающим собственному числу  .
.


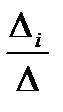 где
где  определитель полученный из определителя матрицы А с заменой i-того столбца столбцом свободных членов.
определитель полученный из определителя матрицы А с заменой i-того столбца столбцом свободных членов.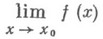 - предел функции в нек-рой точке справа или слева. Пусть f - отображение упорядоченного множества X(напр., множества, лежащего на числовой прямой), рассматриваемого как топологич. пространство с топологией, порожденной отношением порядка, в топологич. пространство Y и
- предел функции в нек-рой точке справа или слева. Пусть f - отображение упорядоченного множества X(напр., множества, лежащего на числовой прямой), рассматриваемого как топологич. пространство с топологией, порожденной отношением порядка, в топологич. пространство Y и  . Предел отображения f по любому интервалу
. Предел отображения f по любому интервалу  наз. пределом слева отображения f и обозначают
наз. пределом слева отображения f и обозначают (он не зависит от выбора
(он не зависит от выбора  ), а предел по интервалу
), а предел по интервалу 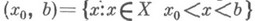 наз. пределом справа и обозначают
наз. пределом справа и обозначают  (он не зависит от выбора
(он не зависит от выбора 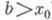 ). Если точка
). Если точка  является предельной как слева, так и справа для множества определения функции f, то обычный предел
является предельной как слева, так и справа для множества определения функции f, то обычный предел функ., действующая из [c,d]в [a,b].Очевидно, что
функ., действующая из [c,d]в [a,b].Очевидно, что  монотонно возрастает. (Если бы функция f была монотонно убывающей, то и обратная к ней функ.
монотонно возрастает. (Если бы функция f была монотонно убывающей, то и обратная к ней функ.  .Тогда обратная к f функ.
.Тогда обратная к f функ. 
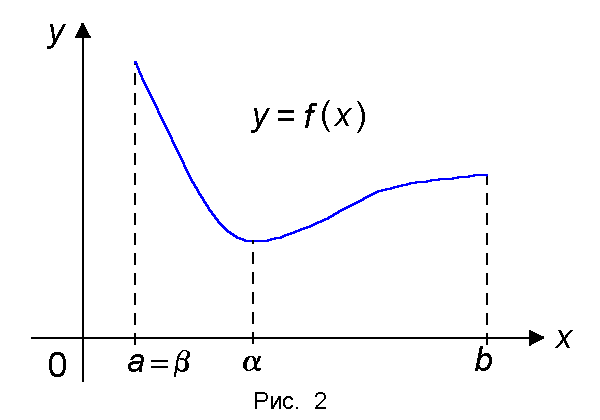

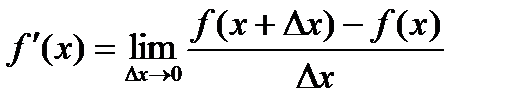
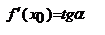 выражает геометрический смысл производной: производная от данной ф. в данной точке = tg угла наклона касательной графика ф-ции в этой тчк.
выражает геометрический смысл производной: производная от данной ф. в данной точке = tg угла наклона касательной графика ф-ции в этой тчк. тангенс угла наклона секущей МР к графику функ.
тангенс угла наклона секущей МР к графику функ. 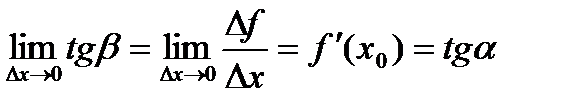 , где a - угол наклона касательной к графику функ. f(x) в точке (x0, f(x0)). Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
, где a - угол наклона касательной к графику функ. f(x) в точке (x0, f(x0)). Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.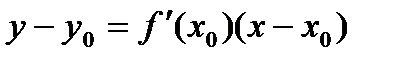
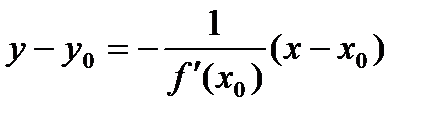 .
.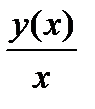 описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af. Среднее приращение, средний прирост, средняя скорость изменения определяется отношением
описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af. Среднее приращение, средний прирост, средняя скорость изменения определяется отношением 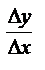 . Производная
. Производная 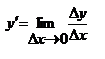 выражает предельные издержки производства. Величину Mf(x) = y' наз. мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определ. предельную выручку, предельный доход, предельную полезность и др. предельные величины.
выражает предельные издержки производства. Величину Mf(x) = y' наз. мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определ. предельную выручку, предельный доход, предельную полезность и др. предельные величины.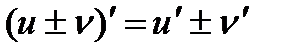 2. Производная произведения двух диффиренц-ых ф-ций = произведению первой ф-ции на производную второй + произведение второй ф-ции на производную первой:
2. Производная произведения двух диффиренц-ых ф-ций = произведению первой ф-ции на производную второй + произведение второй ф-ции на производную первой:  3. Производная частного двухдифференц-ых ф-ций определ. формулой:
3. Производная частного двухдифференц-ых ф-ций определ. формулой: 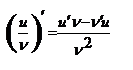 где
где 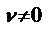
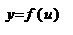 и
и 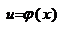 -дифференцируемые ф. своих аргументов, то производная сложной ф.
-дифференцируемые ф. своих аргументов, то производная сложной ф. 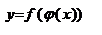 сущ. и равна произведению производной этой ф-ции по промежуточному аргументу на производную промежуточного по независимой переменной, т.е.
сущ. и равна произведению производной этой ф-ции по промежуточному аргументу на производную промежуточного по независимой переменной, т.е. 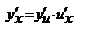 ,
, 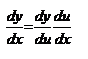 .
.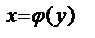 - взимнообратые дифференцируемые ф-ции и
- взимнообратые дифференцируемые ф-ции и  ,то
,то 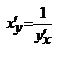 Действительно, т.к.
Действительно, т.к. 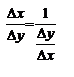 ,то
,то 
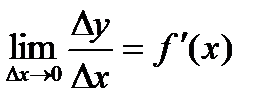 , то
, то , где a®0, при Dх®0. f¢(x)Dx- линейная часть приращения и называется дифференциалом функции и обозначается dy d f (x). dy = f¢(x)dx. Можно также записать:
, где a®0, при Dх®0. f¢(x)Dx- линейная часть приращения и называется дифференциалом функции и обозначается dy d f (x). dy = f¢(x)dx. Можно также записать: 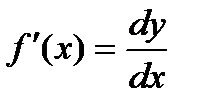

 .
. или
или  . Тогда, если сущ. предел отношения производных этих функ.
. Тогда, если сущ. предел отношения производных этих функ. 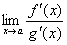 , то сущ. и предел отношения самих функ. f(x)/g(x) при x → а, причем
, то сущ. и предел отношения самих функ. f(x)/g(x) при x → а, причем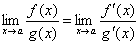
 )<f(
)<f( ;x1
;x1 


