
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточное условие экстремумаСодержание книги Поиск на нашем сайте
Первое достаточное условие экстремума Пусть х0 – точка максимума, т.е. f’(x0)=0 Если f’ при переходе точки х0 меняет знак от + к -, то это точка максимума, если от – к +, то это точка минимума Если f’ не меняет знак при переходе через х0, то это точка перегиба Второе достаточное условие экстремума Пусть y=f(x) X0, f’(x0)=0 (т.е. выполняется необходимое условие экстремума) Если f’’(x0)>0,x0 – точка min f’’(x0)<0,x0 – точка max 46.)Условие выпуклости и вогнутости функции. Точка перегиба. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – наз. вогнутой. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла). Если график функ.находится выше касательной, то график такой ф-ции наз. вогнутым, если график ф-ции ниже касательной - то выпуклой. Если f’’(x)>0, x? (a,b), то ф-ции вогнутая Если f’’(x)<0, x? (a,b), то ф-ции выпуклая Если f’’(x)=0, x? (a,b), то х – точка перегиба, т.е. при переходе через х ф-ция меняет выпуклость Точка, отделяющая выпуклую часть кривой от вогнутой, наз. точкой перегиба. В точке перегиба касательная пересекает кривую. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не сущ. и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а явл. точкой перегиба. Асимптоты. Прямая наз. асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.Асимптоты могут быть прямые и наклонные. Кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, Вертикальные асимптоты. Из определения асимптоты следует, что если Наклонные асимптоты.
Построение графиков ф-ции 1. Находим область допустимых значений 2. Находим стационарные точки (f’=0) 3. Находим область монотонность (возрастания и убывания) 4. Находим точки максимума и минимума Функ. нескольких переменных Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных. z = f(x, y) Геометрическое изображение функции двух переменных - поверхность. Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной Областью определения функции z называется совокупность пар (х, у), при которых функция z существует Окрестностью точки М0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию Число А наз. пределом функ. f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие Записывают: Однородная функция. Функция одного или нескольких переменных f (x 1, x 2, …, xn) называется однородной степени k, если существует такое (постоянное) число k, что при любых значениях λ выполняется тождество 50.)Частной производной функ. нескольких переменных по одной из этих переменных наз. предел отношения соответствующего частного приращения функ. к приращению данной переменной,когда последнее стремится к нулю.Для функ. двух переменных z= f(x,y),полагая,например, y (игрик) постоянной, получаем производную
Полным приращением функции z=f(x,y) наз. разность:
Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции кот. на координатные оси равны значениям функ. u в соответствующей точке При этом говорят, что в области D задано поле градиентов. Производная по направлению.. Рассмотрим функцию u(x, y, z) в точке М(x, y, z) и точке М1(x + Dx, y + Dy, z + Dz). Проведем через точки М и М1 вектор
Далее предположим, что функ. u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:
Приведенные выше равенства могут быть представлены след. образом:
Заметим, что величина s является скалярной. Она лишь определяет направление вектора Предел
51)Необходимые условия экстремума). Если функция f(x,y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю Теорема. (Достаточные условия экстремума). Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение: 1.Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, если 2.Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума В случае, если D = 0, вывод о наличии экстремума сделать ноль
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 или
или  или
или  , то прямая х = а – асимптота кривой y = f(x).
, то прямая х = а – асимптота кривой y = f(x). . прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.
. прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.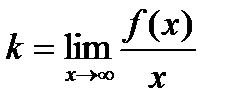 .
. 
 .
. также верно и условие
также верно и условие 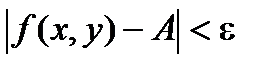 .
.
 =f
=f  x (x,y), кот. наз. частной производной функ. z по переменной х.Аналогично определяется производная функ. z по переменной х:
x (x,y), кот. наз. частной производной функ. z по переменной х.Аналогично определяется производная функ. z по переменной х: = f
= f 
 , то этот вектор наз. градиентом функ. u.
, то этот вектор наз. градиентом функ. u. 
 . Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов наз. направляющими косинусами вектора
. Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов наз. направляющими косинусами вектора 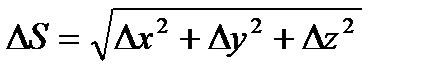
 , где величины e1, e2, e3 – бесконечно малые при
, где величины e1, e2, e3 – бесконечно малые при  . Из геометрических соображений очевидно:
. Из геометрических соображений очевидно: 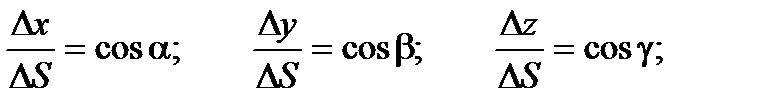
 ;
; 
 наз. производной функ. u(x, y, z) по направлению вектора
наз. производной функ. u(x, y, z) по направлению вектора 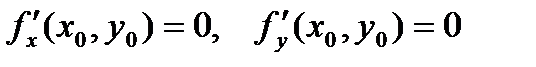 , либо хотя бы одна из них не существует.Эту точку (х0, у0) будем называть критической точкой.
, либо хотя бы одна из них не существует.Эту точку (х0, у0) будем называть критической точкой.
 - максимум, если
- максимум, если  - минимум.
- минимум.


