
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий линейной зависимости векторовСодержание книги Поиск на нашем сайте
Для того чтобы векторы
Размерность и базис линейного пространства, координаты вектора Пусть X — линейное пространство. Определение. Если сущ/ натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью. Будем обозначать n –мерное линейное пространство Xn, где n = dimXn — размерность пространства Xn. Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов. Замечания. 1)Размерность пространства, состоящего только из одного нулевого вектора, равна нулю. Такое пространство называется тривиальным. 2)Если в линейном пространстве сущ/любое число линейно независимых векторов, то такое пространство называется бесконечномерным. Мы будем рассматривать, в основном, конечномерные линейные пространства. Бесконечномерные пространства являются предметом специального изучения.
13) Скалярным произведением (ā,b) двух векторов а и b наз. число, равное произведению длины этих векторов на косинус угла ȹ между ними: (ā,b)= ā*b= │ ā ││b│cos ȹ. Эвклидово пространство- Действительное линейное пространство E называется евклидовым, если каждой паре векторов 1. 2. 3.
14.Пусть плоскость Q проходит через точку М0 (x0,y0,z0) перпендикулярно вектору n =(А,В,С). Этими условиями определяется единственная плоскость в пространстве Оxyz.Вектор n называется нормальным вектором плоскости Q. Возьмём в плоскости Q произвольную точку М(x,y,z). Тогда вектор М0М =(x-x0,y-y0, z-z0),будет перпендикулярен вектору n=(А,В,С). Следовательно, скалярное произведение этих векторов равно нулю, т.е. (n, М0М)=0 Представим уравнение плоскости,перпендикулярной данному вектору и проходящей через данную точку М0 (x0,y0,z0) А(x-x0)+В(y-y0)+С(z-z0)= 0 Уравнение плоскости,записанное в виде Ax + By + Cz + D=0,где D= -Ax0 -By 0-Cz 0 ,называется общим уравнением плоскости. 15) Угол между плоскостями Пусть плоскости П1 и П2 заданы соответственно уравнениями
Требуется найти угол альфа между этими плоскостями.
Рис.11.6.Угол между плоскостями Если через точку
Рис.11.8.Угол между нормальными векторами тупой
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула позволяет найти косинус острого угла между плоскостями. Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей: Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
16)Ур/ прямой в пространстве, проходящей через две точки A(x0,y0,z0) и B(x1,y1,z1)наз. равенство:
Угол между двумя прямыми равен углу между их направляющими векторами. Если прямые заданы след. урав:A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0 тогда направляющие векторы этих прямых будут равны: a1 = (- B1; A1) и a2 = (- B2; A2) Воспользуемся формулой скалярного произведения двух векторов:
из этой формулы получим:
Выразим угол φ:
Из последней формулы получим:
Если прямые параллельны, то k1=k2 и b1≠b2 Если прямые перпендикулярны, то k1*k2=-1
Если прямые пересекаются, то k1≠k2 Если прямые совпадают, то k1=k2 и b1=b2
Матрицы Матрицей А размера m на n наз.прямоугольная таблица из m строк и n столбцов,состоящая из чисел или иных матем.выражений Операции над матрицами Суммой матриц А= Произведение матриц А= Свойства операции умножения1)(A B)C=A(BC)=ABC 2)(A+B)C=AC+BC 3)A(B+C)=AC+BC 4)AB Транспонированной к матрице А= Диагональная матр., у кот. все элементы на главной диагонали равны 1, наз. единичной матрицей (Е).
Определители Определитель 2-го порядка задаётся равенством: Определитель 3-го порядка задаётся равенством: Определитель3-го порядка есть сумма 6=3! Слагаемых,каждое из которых представляет собой произведение 3-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одна половина слагаемых берётся со знаком +,другая со знаком -. 19)Алгеброическим дополнением Определитель n-го порядка задаётся равенством:
Сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одна половина слагаемых берется со знаком +,другая мо знаком -. 20)Обратной матрицей к квадратной матрице А наз.такая матрица,что Если квадратеая матрица А-невырожденная,то Алгоритм нахождения:1)Вычислим определитель матрицы А,если опр.=0,то обратная матрица не сущ.2)Если опред.не равен 0,то обратная матрица сущ.Находим алгеброическое дополнение 21) Пусть K - поле, 22)Системы линейных уравнений. Система m линейных алгебраических уравнений с n неизвестными в линейной алгебре — это система уравнений вида
Здесь m — колич. Урав., а n — колич. неизвестных. Система линейных урав. может быть представлена в матричной форме как: Правило Крамера.Если определитель матрицы А отличен от 0, то система имеет единственное решение определяемое из форм.Xi=
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.81.158 (0.01 с.) |

 (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
 сопоставляется число
сопоставляется число  так, что
так, что  и
и  выполняются аксиомы:
выполняются аксиомы:



 и
и  .
. Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку
Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку  на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры l1 и l2 к линии пересечения. Нарисуем также нормальные векторы n1 и n2 плоскостей П1 и П2 с началами в точке
на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры l1 и l2 к линии пересечения. Нарисуем также нормальные векторы n1 и n2 плоскостей П1 и П2 с началами в точке  , перпендикулярную линии пересечения плоскостей П1 и П2, то прямые l1 и l2 и изображения векторов n1 и n2 будут лежать в этой плоскости. Сделаем чертеж в плоскости
, перпендикулярную линии пересечения плоскостей П1 и П2, то прямые l1 и l2 и изображения векторов n1 и n2 будут лежать в этой плоскости. Сделаем чертеж в плоскости  Рис.11.7.Угол между нормальными векторами острый
Рис.11.7.Угол между нормальными векторами острый В одном варианте (рис. 11.7)
В одном варианте (рис. 11.7)  и
и  , следовательно, угол
, следовательно, угол  между нормальными векторами равен углу
между нормальными векторами равен углу  , являющемуся линейным углом острого двугранного угла между плоскостями П1 и.Во втором варианте (рис. 11.8)
, являющемуся линейным углом острого двугранного угла между плоскостями П1 и.Во втором варианте (рис. 11.8)  , а угол
, а угол  . Так как
. Так как  то в обоих случаях
то в обоих случаях  .По определению скалярного произведения
.По определению скалярного произведения  . Откуда
. Откуда 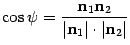 и соответственно
и соответственно 

 где
где  -- любое число.
-- любое число.




 .Квадратной матрицей n-го порядка наз.матрица размера n на n.Диагональной наз.квадратная матрица,у котрой все элементы вне главной диагонали равны 0.Единичной наз.диагональная матрица с единицами на главной диагонали.Нулевой наз.матрица,все элементы которой равны 0.
.Квадратной матрицей n-го порядка наз.матрица размера n на n.Диагональной наз.квадратная матрица,у котрой все элементы вне главной диагонали равны 0.Единичной наз.диагональная матрица с единицами на главной диагонали.Нулевой наз.матрица,все элементы которой равны 0. и B=
и B= 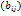 одинакового размера наз.матрица С=
одинакового размера наз.матрица С=  того же размера.Свойства операции сложения матриц.Для любых матриц А,B,C одного размера выполняются равенства:1)A+B=B+A 2)(A+B)+C=A+(B+C)=A+B+C
того же размера.Свойства операции сложения матриц.Для любых матриц А,B,C одного размера выполняются равенства:1)A+B=B+A 2)(A+B)+C=A+(B+C)=A+B+C
 =(
=( ) такая,что
) такая,что  .Элемент строки матрицы назовём крайним,если он отличён от 0,а все элементы этой строки,находящиеся левее него,равны 0.Матрица наз.ступенчатой,если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки
.Элемент строки матрицы назовём крайним,если он отличён от 0,а все элементы этой строки,находящиеся левее него,равны 0.Матрица наз.ступенчатой,если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки ).Опредилитель 2-го порядка есть сумма 2=2!слагаемых,каждое из кот. представляет собой произведение 2-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одно из слогаемых берется со знаком +,другое-со знаком -.
).Опредилитель 2-го порядка есть сумма 2=2!слагаемых,каждое из кот. представляет собой произведение 2-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одно из слогаемых берется со знаком +,другое-со знаком -.
 к элементу
к элементу  квадратной матрицы А=
квадратной матрицы А=  наз.произведение
наз.произведение  *
* 
 =
=  .Указанная сумма состоит из n!слагаемых,каждое из которых представляет собой произведение
.Указанная сумма состоит из n!слагаемых,каждое из которых представляет собой произведение
 *А=А*
*А=А*  =
=  ,получ.транспонированием из матрицы,составленной из алгебраических дополнений
,получ.транспонированием из матрицы,составленной из алгебраических дополнений 
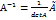 .
. элементов матрицы А и составляем матрицу из них
элементов матрицы А и составляем матрицу из них  3)Транспонируем матрицу
3)Транспонируем матрицу  4)Находим обратную матрицу по формуле
4)Находим обратную матрицу по формуле  5)Осущ.проверку А*
5)Осущ.проверку А* 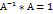
 ,
, 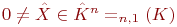 ,
,  . Если
. Если  , то
, то  называется собственным числом матрицы A, а
называется собственным числом матрицы A, а  - собственным вектором матрицы A, отвечающим собственному числу
- собственным вектором матрицы A, отвечающим собственному числу  .
.


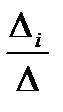 где
где  определитель полученный из определителя матрицы А с заменой i-того столбца столбцом свободных членов.
определитель полученный из определителя матрицы А с заменой i-того столбца столбцом свободных членов.


