
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первоообразная функции и неопределённый интегралСодержание книги Поиск на нашем сайте
Пусть функ. f(х) определена не некотором интервале (а,b).Тогда функция F(x) наз.первообразной для функции f(х) на интервале (а,b),если F’(x) для всех х Совок. всех первообразных для функ. f(x) наз.неопределённым интегралом от функ. f(x).Знак Свойства неопределённого интеграла 1) Метод замены переменной Если нахождение интеграла Интегрирование по частям Пусть функ. u(x) и v(x) непрерывны вместе со своими производными на множестве X и на этом множестве сущ.интеграл Для интегралов вида В случае интегралов вида
Интегрирование простейших рац. дробей Целой рац. Функ. аргумента х наз. многочлен, в кот. переменная х только в целых степенях (в том числе х =1).anxn + an-1xn-1 +... + a2x2 + a1x + a0. Дробной рац. Функ. аргумента х наз. отношение целых рац.функ.. Причем если степень числителя меньше степени знаменателя, дробь наз. правильной. В противном случае - неправильной. Алгоритм: 1. Если дробь неправильная - выделить целую часть. Получим интеграл от целой части (интегрируется непосредственно) и интеграл от правильной дроби;2. Если числитель равен дифференциалу знаменателя (или отличается от него постоянным множителем), то использовать замену переменной z=знаменатель;3. Если числитель равен дифференциалу некого многочлена (или отличается от него постоянным множителем), а знаменатель равен степени того же многочлена, то использовать замену переменной z=знаменатель;4 В остальных случаях нужно разложить дробь на сумму простейших Интегрирование рациональных дробей Функ. вида R(x)= Алгоритм интегрирования рац.функций 1)Если рац.дробь неправильная,то путём деления числителя на знаменатель по правилу деления многочленов следует выделить целую часть и представить дробь в виде 2)Разложить знаменатель 3)Разложить правильную дробь 4)Найти неизвестные коэффициенты в разложении(предыдущий) 5)Почленно проинтегрировать каждую простейшую дробь Интегрирование иррациональных функций 1)Интеграл вида Интегрирование тригонометрических функций Интегралы вида 1)Если R(sinx,cosx)-нечётная функ.относительно sinx,т.е.если R(-sinx,cosx)=- R(sinx,cosx),то интеграл рационализируется подстановкой cosx=t 2) Если R(sinx,cosx)-нечётная функ.относительно cosx,т.е.если R(sinx,-cosx)=- R(sinx,cosx),то интеграл рационализируется подстановкой sinx=t 3) Если R(sinx,cosx)-чётная функ.относительно sinx и cosx,т.е.если R(-sinx,-cosx)= R(sinx,cosx),то применяется подстановка tgx=t При вычислении интегралов Определенный интеграл. Если сущ.конечный предел интегральной суммы при n→∞, Δх →0 независимо от способа разбиения, независимо от выбора точек
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.67 (0.005 с.) |

 (а,b)
(а,b) наз.интегралом,функция f(x)-подынтегральной функціей,а f(x)dx-подынтегральным выражением.Операция нахождения неопределённого интеграла от данной функ. наз.интегрированием этой функции.
наз.интегралом,функция f(x)-подынтегральной функціей,а f(x)dx-подынтегральным выражением.Операция нахождения неопределённого интеграла от данной функ. наз.интегрированием этой функции. =F(x)+C 2)d
=F(x)+C 2)d 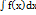 =f(x)dx 3)
=f(x)dx 3)  4)
4)  5)Если
5)Если  F(ax+b)+с
F(ax+b)+с затруднительно,то пользуются методом подстановки или методом замены переменной.При применении этого метода используют подстановки двух видов:1) x=
затруднительно,то пользуются методом подстановки или методом замены переменной.При применении этого метода используют подстановки двух видов:1) x=  (t),где х=
(t),где х=  (t)-монотонная непрерывно дифференцируемая фун.новой переменной t.В этом случае
(t)-монотонная непрерывно дифференцируемая фун.новой переменной t.В этом случае  2)u=
2)u=  ,где u-новая переменная.Формула замены переменной при такой подстановке:
,где u-новая переменная.Формула замены переменной при такой подстановке: 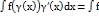 (
( .
.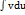 .Тогда на этом множестве сущ. интеграл
.Тогда на этом множестве сущ. интеграл  и справедлива формула интегрирования по частям
и справедлива формула интегрирования по частям 
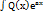 dx,
dx,  ,
, 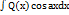 ,где Q(x)-многочлен,в качестве u следует брать Q(x),а в качестве dv –выражение
,где Q(x)-многочлен,в качестве u следует брать Q(x),а в качестве dv –выражение  dx
dx  .
.
 в качестве u берут функ.lnx,arcsinx, arccosx, arctgx, arcctgx,а в качестве dv-выражение Q(x)dx
в качестве u берут функ.lnx,arcsinx, arccosx, arctgx, arcctgx,а в качестве dv-выражение Q(x)dx ,где
,где 
 -многочлены соответственно степени m и n,наз.рациональной функ.Интегрирование рац.функ. с помощью метода разложения на простейшие дроби сводится к интегрированию многочленов и простейших рациональных функ.след.4-х видов:1)
-многочлены соответственно степени m и n,наз.рациональной функ.Интегрирование рац.функ. с помощью метода разложения на простейшие дроби сводится к интегрированию многочленов и простейших рациональных функ.след.4-х видов:1)  ; 2)
; 2) 

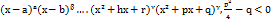
 на сумму простейших дробей:
на сумму простейших дробей:  =
=  +….
+….  +
+ 
 подстановкой
подстановкой  приводится к интегралу от рациональной функции t 2) Интеграл вида
приводится к интегралу от рациональной функции t 2) Интеграл вида 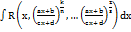 рационализируется с помощью подстановки
рационализируется с помощью подстановки 

 -рациональная функ.от
-рациональная функ.от  cosx, приводятся к интегралам от рац.функций с помощью универсальной тригон.подстановки tg
cosx, приводятся к интегралам от рац.функций с помощью универсальной тригон.подстановки tg 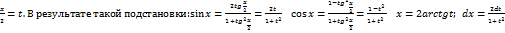
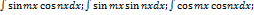 используются формулы 1)
используются формулы 1)  2)
2) 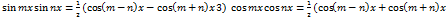
 , то этот предел наз. определённым интегралом данной функ.,а функ. - интегрируемой
, то этот предел наз. определённым интегралом данной функ.,а функ. - интегрируемой


