
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
определение однородного дифференциального уравненияСодержание книги
Поиск на нашем сайте
Дифференциальное уравнение первого порядка
Наз. однородным, если правая часть удовлетворяет соотношению
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
Однородное дифференциальное уравнение можно также записать в виде
или через дифференциалы:
где P(x,y) и Q(x,y) − однородные функ. одинакового порядка. 65)Линейные ДУ I порядка. называется уравнение вида у΄+р(х)у=f(x),где р(х) и (х)-заданные непрерывные функции.Решение линейного уравнеия сводиться к решению дифференциальных уравнений с разделяющимеся переменными относительно каждой из вспомогательной функции.
66)Неоднородными дифференциальным урав. второго порядка с постоянными коэффициентами наз. уравнение вида Теорема Пусть y*=
Для нахождения частного решения у* можно использовать специальный вид правой части урав. Будем искать частное решение неоднородного уравнения, используя «метод неопределённых коэффициентов» по след. правилам: 1)Если F(x)=P(x), где P(x)-многочлен степени n, то соответствующее частное решение ищется: а)в виде у*= Q(x),где Q(x) -многочлен степени n с неопределёнными коэффициентами, если ноль не явл. корнем характеристического урав.; б) в виде у*=ха Q(x),где Q(x) - многочлен степени n с неопределёнными коэффициентами, если нуль явл. корнем характеристического урав. кратности 2)Если f(x)=P(x)emx,то соответствующее частное решение находится: а)в виде y*=Q(x)emx,где, где Q(x) - многочлен степени n с неопределёнными коэффициентами, если м не явл. корнем характеристического урав.. б) в виде у*=ха Q(x) emx,где Q(x) - многочлен степени n с неопределёнными коэффициентами, если м явл. корнем характеристического урав. кратности 3)Если f(x)=eax (M а) в виде у*= eax (А Не явл.корнями характеристического уравн. б) в виде у*= eax (А Явл.корнями характеристического урав.
67)Числовым рядом наз.выражение, полученное последовательным сложением членов числовой последовательности Ряд наз.сходящимся, если сущ. конечный предел Простейшие свойства сходящихся рядов. 1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда.Изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости. 2. Если ряд 3. Если ряд 4. Если ряды 5. Если ряд Необходимое условие сходимости ряда. Если ряд
Признаки сходимости рядов с положительными членами Пусть дан ряд Признак Коши. Пусть сущ. Если Признак Даламбера. Пусть сущ. Если Если 69) Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, наз.знакопеременным. Абсолютная и условная сходимость Ряд 70) Частным случаем знакопеременного ряда явл. знакочередующийся ряд, т.е. такой ряд, в кот. последовательные члены имеют противоположные знаки. Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} явл. числовой последовательностью, такой, что 1. 1.an+1 < an для всех n; 2. 2. Тогда знакочередующиеся ряды
71)Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
Теорема Абеля: Пусть ряд Пусть ряд Радиус сходимости:
Если
72)
|
||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.31.223 (0.009 с.) |






 , где p и q- постоянные,
, где p и q- постоянные,  – функ., непрерывная на некотором множестве Х.
– функ., непрерывная на некотором множестве Х. -некоторое частное решение исходного неоднородного уравнения, а
-некоторое частное решение исходного неоднородного уравнения, а 0 = C1 y 1 (x) + C 2 y 2 (x)- общее решение соответствующего однородного уравнения. Тогда уобщ =у0 +у* -общее решение неоднородного урав..
0 = C1 y 1 (x) + C 2 y 2 (x)- общее решение соответствующего однородного уравнения. Тогда уобщ =у0 +у* -общее решение неоднородного урав.. .
. , где М и N –const, то у* находится:
, где М и N –const, то у* находится: ,где А,В-постоянные,если числа
,где А,В-постоянные,если числа 
 т.е.
т.е.  й частичной суммой ряда наз.
й частичной суммой ряда наз. 
 явл. суммой ряда; расходящимся, если
явл. суммой ряда; расходящимся, если 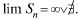 Числа
Числа  — члены ряда,
— члены ряда,  —
—  й или общий член.
й или общий член.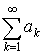 сходится, то
сходится, то  .
. и имеет место равенство
и имеет место равенство  .
. сходятся, то сходится и ряд
сходятся, то сходится и ряд  имеет место равенство
имеет место равенство 
 . Отсюда следует Признак расходимости ряда. Если
. Отсюда следует Признак расходимости ряда. Если  , то ряд
, то ряд  сходится, то
сходится, то  (при
(при  )..
).. .
. . Тогда если с<1, то ряд
. Тогда если с<1, то ряд  , то ряд
, то ряд 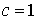 , то о сходимости или расходимости ряда ничего сказать нельзя.
, то о сходимости или расходимости ряда ничего сказать нельзя. . Тогда если
. Тогда если  , то ряд
, то ряд  , то ряд
, то ряд  , то о сходимости или расходимости ряда ничего сказать нельзя
, то о сходимости или расходимости ряда ничего сказать нельзя наз. абсолютно сходящимся, если ряд
наз. абсолютно сходящимся, если ряд  также сходится. Если ряд
также сходится. Если ряд 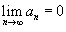 .
. и
и  сходятся.
сходятся.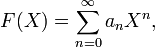 в кот. коэффициенты
в кот. коэффициенты  берутся из некоторого
берутся из некоторого  .
. сходится в точке
сходится в точке  . Тогда этот ряд сходится при всех x так, что
. Тогда этот ряд сходится при всех x так, что  .
. , тогда он расходится при всех х так, что
, тогда он расходится при всех х так, что 

 , то ряд расходится, поскольку общий член ряда
, то ряд расходится, поскольку общий член ряда  не стремится к 0. И наоборот.
не стремится к 0. И наоборот.
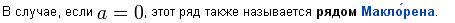
 с точностью до 0,001.
Воспользуемся разложением
с точностью до 0,001.
Воспользуемся разложением  Тогда
Тогда 


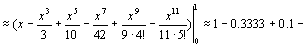 0,0238+0,0046–0,0008≈0,7475≈0,748.
Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
0,0238+0,0046–0,0008≈0,7475≈0,748.
Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.



