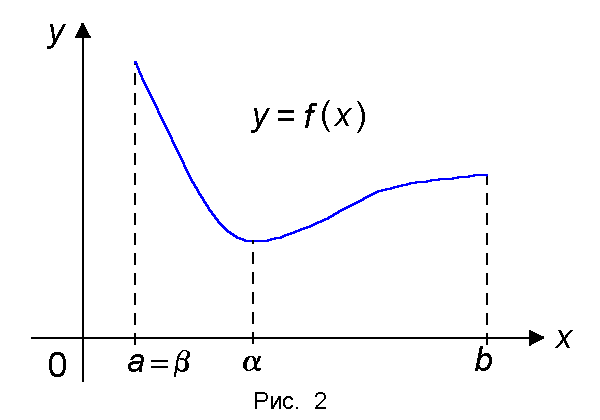Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые величины и их св-ваСодержание книги Поиск на нашем сайте
Функ. f(x) наз. бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если БЕСКОНЕЧНО БОЛЬШАЯ ФУНК. – функ. переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функ.f(x), определенная в окрестности точки х0, наз. бесконечно большой функ. при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:
Аналогичным образом определяются
означает, что для любого М > 0 найдется такое δ = δ (M) > 0, что для всех z < - δ выполняется неравенство f(x) > M. Изучение Б. б. ф. может быть сведено к изучению бесконечно малых функ., т. к. если f(x) есть Б. б. ф., то функция ψ (х) = 1/f(x) явл. бесконечно малой. Непрерывность функции в точке. Определение 1: Функ. f(x) наз. непрерывной функ. в точке A, если сущ. предел данной функ. при аргументе стремящимся к A и он равен f(a), т.е.
Критерий непрерывности:
Для любого сколь угодно малого числа эпсилон, сущ. такое число дельта, зависящее от эпсилон, что из того, что для любых иксов удовлетворяющих неравенству следует, что отличия значений функ. в данных точках будет сколь угодно мало. Критерий непрерывности функции в точке: Функ. будет непрерывна в точке A тогда и только тогда, когда она будет непрерывна в точке A и справа и слева, т.е чтобы в точке A сущест. два односторонних предела, они были равны между собой и равнялись значению функ. в точке A. Определение 2: Функ.непрерывна на множестве, если она непрерывна во всех точках этого множества. Непрерывность сложной функции и обратной функции. Пусть функ. j(t) непрерывна в точке t0 и функ. f(x) непрерывна в точке х0=j(t0). Тогда функ. f(j(t)) непрерывна в точке t0. Доказательство. Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем
Выписывая подчеркнутые кванторы, получим, что
что и говорит о том, что f(j(t)) непрерывна в точке t0. < Обратите внимание на следующие детали: а) т.к. x=j(t), то |j(t)-j(t0)|<d может быть записано как |x-x0|<d, и f(x) превращается в F(j(t)); б) при определении непрерывности j(t) в точке t0 в первом кванторе стоит буква d. Это необходимо для согласования с квантором в предыдущей строке и взаимного уничтожения
Обратная Пустьf(x)-- функ, непрерывная на отрезке [a,b].Предположим, что f(x) монотонна на [a,b]; пусть, для определённости, она монотонно возрастает: из x1<x2, следует, что f (x1)< f (x2) Тогда образом отрезка [a,b] будет отрезок [c,d], где c=f(a), d=f(b)(действительно, непрерывная функ. принимает любое промежуточное между f(a), f (b)значение, причём ровно один раз, что следует из монотонности). Поэтому сущ. обратная к y =f(x) функ. Теорема. Пусть f -- непрерывная монотонная функция, Непрерывность элементарных функций Все элементарные функ. явл. непрерывными в любой точке свой области определения. Функ.наз. элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функ. Множество основных элементарных функ. вкл. в себя: 1.Алгебраические многочлены 2.Рациональные дроби 3.Степенные функ. xp 4.Показательные функ. ax 5.Логарифмические функ. 6.Тригонометрические функ. 7.Обратные тригонометрические функции
36) Теорема 3 (теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном множестве функ. достигает на нем своего наибольшего и наименьшего значений. Непрерывность функ. на отрезке Функ. f (x) наз. непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала. Функ. f (x) наз. непрерывной на отрезке [ a, b ], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b. Замечание. Функ., непрерывная на отрезке [ a, b ] может быть разрывной в точках a и b (рис. 1)
Множество функ., непрерывных на отрезке [ a, b ] обозначается символом C [ a, b ]. Свойства функ., непрерывных на отрезке Теорема 1 (об ограниченности непрерывной функции). Если функ. f (x) непрерывна на отрезке [ a, b ], то она ограничена на этом отрезке, т.е. существует такое число C > 0, что " x О[ a, b ] выполняется неравенство | f (x)| ≤ C. Теорема 2 (Вейерштрасс). Если функ. f (x) непрерывна на отрезке [ a, b ], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. сущ. точки α, β О [ a, b ] такие, что m = f (α) ≤ f (x) ≤ f (β) = M для всех x О [ a, b ] (рис.2).
Наибольшее значение M обозначается символом max x О [ a, b ] f (x), а наименьшее значение m — символом min x О [ a, b ] f (x). Теорема 3 (о существовании нуля). Если функ. f (x) непрерывна на отрезке [ a, b ] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f (ξ) = 0. Геометрический смысл теоремы состоит в том, что график функ., удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).
Теорема 4 (Больцано–Коши). Если функция f (x) непрерывна на отрезке [ a, b ], то она принимает на (a, b) все промежуточные значения между f (a) и f (b). Существование непрерывной обратной функции Пусть функ. y = f (x) определена, строго монотонна и непрерывна на отрезке [ a, b ]. Тогда на отрезке [ α, β ] (α = f (a), β = f (b)) существует обратная функция x = g (y), также строго монотонная и непрерывная на отрезке (α, β).
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.006 с.) |

 .Бесконечно малой функ. может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет. Пример. Функ. f(x) = xn явл. бесконечно малой при х®0 и не явл. бесконечно малой при х®1, т.к.
.Бесконечно малой функ. может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет. Пример. Функ. f(x) = xn явл. бесконечно малой при х®0 и не явл. бесконечно малой при х®1, т.к.  . Теорема. Для того, чтобы функ. f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + a(x),где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).
. Теорема. Для того, чтобы функ. f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + a(x),где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).
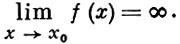

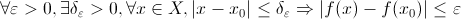


 Любая другая буква на этом месте не дала бы верного результата.
Любая другая буква на этом месте не дала бы верного результата. функ., действующая из [c,d]в [a,b].Очевидно, что
функ., действующая из [c,d]в [a,b].Очевидно, что  монотонно возрастает. (Если бы функция f была монотонно убывающей, то и обратная к ней функ.
монотонно возрастает. (Если бы функция f была монотонно убывающей, то и обратная к ней функ.  .Тогда обратная к f функ.
.Тогда обратная к f функ.