
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение главных компонент тензора инерцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте С ПОМОЩЬЮ МАХОВОГО КОЛЕСА И ПОСТРОЕНИЕ ЭЛЛИПСОИДА ИНЕРЦИИ Идея определения момента инерции махового колеса с помощью вспомогательного тела правильной геометрической формы изложена в работе 22. В данной работе ставится обратная задача - определение момента инерции не махового колеса, а тела, прикрепляемого к нему. Момент инерции махового колеса I к связан с центральным моментом инерции I 01 прикрепленного тела соотношением (см. уравнения (13)-(14) в работе 22)
где m 1 - масса тела, g - ускорение свободного падения, d - расстояние от центра масс тела до оси вращения, T 1 - период колебаний махового колеса с закрепленным на нем телом. Аналогично для другого тела с массой m 2:
Зная момент инерции одного из тел, например I 01, можно экспериментально определить момент инерции другого тела, используя формулу:
Величины m 1, m 2, T 1, T 2, d находятся путем измерения. Приборы и принадлежности: маховое колесо с электронной системой отсчета времени, исследуемое и вспомогательное тела, штангенциркуль, весы. ХОД РАБОТЫ 1. Найдите взвешиванием массу m 1 вспомогательного тела и определите штангенциркулем его размеры. Рассчитайте момент инерции I 01 по соответствующей формуле из таблицы 1. 2. Укрепите вспомогательное тело на маховом колесе. 3. Включите установку в сеть переменного тока 220 В. Нажмите последовательно кнопки «Сеть» и «Сброс» на панели установки. Если установка исправна, на табло появятся нули. 4. Качните колесо и измерьте время 10-15 колебаний, запуская миллисекундомер кнопкой «Cброс»и останавливая его кнопкой«Cтоп». Вычислите период колебаний T 1. 5. Прикрепите вместо вспомогательного тела исследуемое так, что бы главная ось его тензора инерции была параллельна оси вращения повторите пункты 4,5. Найдите период колебания T 2. 6. Рассчитайте момент инерции исследуемого тела по формуле (30). 7. Аналогично определите две другие главные компоненты тензора инерции. 8. Измерьте размеры исследуемого тела. 9. Самостоятельно выберите какую-либо неглавную ось исследуемого тела и по формуле (20) рассчитайте момент инерции относительно нее. Сравните полученные результаты. 10.Постройте эллипсоид инерции. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАБОТЕ 1. Ответьте на вопросы 1-6 из предыдущей работы. 2. Выведите формулу (30). Какие допущения использованы в этой формуле? Какие условия эксперимента и особенности установки делают их обоснованными? 3. Каким должно быть оптимальное соотношение между моментами инерции махового колеса и исследуемого тела? ЛАБОРАТОРНАЯ РАБОТА N 26. ИЗУЧЕНИЕ СВОЙСТВ ГИРОСКОПА
Гироскопом называется симметричный волчок (т.е. твердое тело, у которого совпадают по крайней мере два главных значения тензора инерции Так как ось вращения совпадает с осью симметрии гироскопа, то его момент импульса равен: L =I3 w, (31) где I 3 - момент инерции гироскопа относительно оси 3, w - угловая скорость вращения. Из выражения (31) видно, что ось вращения совпадает с направлением вектора момента импульса гироскопа L. Приближенная теория движения гироскопа полагает, что малые по величине моменты внешних сил не могут изменить величину момента импульса L, а меняют только его направление. Момент импульса гироскопа подчиняется основному закону вращательного движения:
где M - суммарный момент внешних сил. Рассмотрим это уравнение применительно к гироскопу, закрепленному в одной точке. Допустим, что точка приложения силы лежит на оси симметрии (см. рис. 7), а сила направлена перпендикулярно оси симметрии 3. Тогда момент этой силы направлен перпендикулярно к оси вращения и L. Под действием момента постоянной силы, вектор L, а следовательно и ось гироскопа, должны совершать равномерное вращение вокруг оси 1. Это вращение называется вынужденной прецессией. Угловая скорость прецессии W может быть найдена из следующих соображений. Поскольку вектор L не меняет своей длины, то изменение этого вектора d L за время dt обусловлено исключительно его вращением со скоростью W и определяется выражением:
Из сравнения уравнений (32) и (33) имеем:
или в скалярном виде для данного случая:
откуда
Следовательно, при закреплении только одной точки ось гироскопа может совершать движение в пространстве в любом направлении в зависимости от направления момента внешней силы. Такой гироскоп называется свободным. Угловая частота прецессии свободного гироскопа прямо пропорциональна моменту внешней силы и обратно пропорциональна частоте вращения гироскопа вокруг оси симметрии. Целью данной работы является наблюдение прецессии гироскопа и экспериментальная проверка уравнения (34). ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
На основании 1, (см. рис. 8) оснащенном ножками с регулируемой высотой закреплена колонна 2. С помощью ножек можно произвести выравнивание прибора по горизонтали. На колонне имеется кронштейн 3 с фотоэлектрическим датчиком 4 и внешней втулкой вращательного соединителя 5. Соединитель 5 позволяет гироскопу вращаться вокруг вертикальной оси и обеспечивает электрическое питание фотоэлектрического датчика 6 и электродвигателя 7. Электродвигатель смонтирован на кронштейне 8 таким образом, что имеется возможность его ограниченного поворота в вертикальной плоскости. На валу двигателя закреплен диск 9, защищенный кожухом 10. На рычаге 11, с нанесенной на нем метрической шкалой, крепится противовес 12. Перемещением противовеса по рычагу можно либо создать внешний вращательный момент М, либо уравновесить гироскоп. Угол поворота вокруг вертикальной оси можно определить по шкале 13 с помощью указателя 14, или с помощью блока управления и измерений 15. Шкала 13 имеет отверстия через каждые 5°, которые позволяют с помощью фотодатчика 4 определить угол поворота гироскопа. Этот угол высвечивается на индикаторе 16. Диск 9 имеет на окружности отверстия, которые подсчитываются с помощью фотоэлектрического датчика 6 и по индикатору 17 можно определить угловую скорость вращения диска. Ее можно регулировать с помощью ручки 18. Время прецессии фиксируется на индикаторе 19. Нажатие клавиши «Сеть» 20 вызывает включение питающего напряжения. При нажатии клавиши «Сброс» 21 осуществляется перевод блока измерений в исходное нулевое состояние. Нажатием клавиш «Стоп» можно остановить отсчет угла и времени прецессии. ХОД РАБОТЫ ВНИМАНИЕ! Раскрученный гироскоп обладает большим запасом кинетической энергии. ПРИ ПРОВЕДЕНИИ УПРАЖНЕНИЙ СТРОГО СЛЕДУЙТЕ ПРИВЕДЕННЫМ НИЖЕ УКАЗАНИЯМ. 1. Перед началом работы убедитесь, что рычаг 11 с гироскопом может свободно вращаться вокруг горизонтальной и вертикальной осей. 2. С помощью ножек с регулируемой высотой и уровня 23 установите прибор горизонтально. 3. Перемещением противовеса 12 добейтесь, чтобы рычаг 11 занял горизонтальное положение. 4. Ручку «Регулятор скорости» на панели прибора переведите в крайнее левое положение. 5. Включите прибор клавишей «Сеть». При этом загораются табло индикаторов и лампочки фотодатчиков. 6. Плавно (!) поворачивая «Регулятор скорости», включите электродвигатель и установите скорость вращения гироскопа около 5000 об/мин. В течение всего эксперимента скорость вращения гироскопа изменять не следует. 7. Легким постукиванием рукой по кончику рычага 11 убедитесь в том, что ось гироскопа не меняет своего направления в пространстве. 8. Закрепите вертикальную ось гироскопа винтом 24. Слегка покачивая ось гироскопа, убедитесь, что она легко меняет свое направление в вертикальной плоскости. 9. По метрической шкале рычага 11 определите положение l 0 противовеса 12 при уравновешенном гироскопе. 10.Освободите вертикальную ось гироскопа винтом 24. При этом не должно наблюдаться прецессии. 11.Смещением противовеса по рычагу на расстояние 12.С помощью секундомера и шкалы 16 определите угловую скорость прецессии 13.Повторите пункты 11 и 12 для других положений противовеса (не менее 4-х). 14.Из формулы (34) следует, что M = I wW, т.е. график зависимости вращающего момента М от произведения wW является прямой с тангенсом угла наклона равным моменту инерции гироскопа. Постройте этот график и определите момент инерции гироскопа. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАБОТЕ 1. Изучите приближенную теорию гироскопа. 2. Расскажите о применении гироскопов в технике. 3. В чем на ваш взгляд отличие прецессионного движения от других движений под действием внешних сил? 4. Расскажите о цели работы и полученных результатах. 5. Вы убедились (см. «Ход работы» пункт 7), что если вертикальная ось уравновешенного гироскопа свободна, его ось симметрии не меняет своего направления в пространстве при легких постукиваниях по штоку. Объясните причину такой устойчивости гироскопа. Почему, если вертикальная ось закреплена (пункт 8) гироскоп теряет устойчивость. 6. Объясните, почему с течением времени ось прецессирующего гироскопа выходит из горизонтальной плоскости? ЛАБОРАТОРНАЯ РАБОТА N 27. МАЯТНИК МАКСВЕЛЛА Цель работы - изучение вращательного движения и метода определения момента инерции металлических колец с помощью маятника Максвелла. Маятник Максвелла - это массивный диск, насаженный на ось, на которую с двух сторон намотаны нити. Под действием сил тяжести и натяжения нитей маятник опускается, убыстряя вращение. Это длится до тех пор, пока нити не размотаются на полную длину. Сообщив “рывок” нитям, маятник продолжает вращаться в том же направлении и, наматывая нити на ось, поднимается вверх. Достигнув верхней точки, диск опять начнет опускаться вниз и т.д. Таким образом, имеет место колебательное движение диска маятника Максвелла вверх и вниз. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА Приборы и принадлежности: маятник Максвелла, металлические кольца, штангенциркуль, весы.
Основание прибора 1 (см. рис. 9) оснащено регулируемыми ножками 2, которые позволяют произвести его горизонтальное выравнивание. В основании закреплена колонна 3, к которой прикреплен неподвижный верхний кронштейн 4 и подвижный нижний кронштейн 5. На верхнем кронштейне находится электромагнит 6, первый фотоэлектрический датчик 7 и вороток 8 для закрепления и регулирования бифилярной подвески маятника. Нижний кронштейн вместе с прикрепленным к нему вторым фотоэлектрическим датчиком 9 можно перемещать вдоль колонки и фиксировать в произвольно избранном положении. На диск маятника 10 надеваются сменные кольца 11. Маятник с одним из сменных колец удерживается в верхнем положении электромагнитом. Длина маятника измеряется по миллиметровой шкале на колонне прибора. С целью облегчения этого измерения нижний кронштейн оснащен указателем, помещенным на высоте оптической оси нижнего фотоэлектрического датчика. Фотоэлектрический датчик соединен с электронным миллисекундомером 12. Время падения диска маятника t связано с его массой m и моментом инерции I соотношением:
где L - длина нитей d - диаметр оси. Момент инерции маятника равен сумме моментов инерции диска, оси и кольца I=I д +I o +I к, а его масса, соответственно m=m д +m o +m к (массы указаны на самих деталях). Соотношение (35) легко получить, решая совместно уравнение движения центра масс: ma = mg - T (36) и уравнение вращательной динамики относительно горизонтальной оси, проходящей через центр масс маятника:
где а - ускорение центра масс, b - угловое ускорение диска, T - сила натяжения нити. При этом надо иметь ввиду, что для плотной намотки нерастяжимой нити ускорение а связано с угловым ускорением b соотношением b d = 2 a, и что при равноускоренном падении путь s зависитот времени по закону:
ХОД РАБОТЫ 1. Проведите необходимые измерения размеров оси и диска и вычислите их моменты инерции I о, I д по соответствующим формулам из табл. 1. 2. Установите прибор горизонтально, регулируя длину ножек 2 (см. рис. 9). 3. Наденьте на диск 10 сменное кольцо 11. 4. Проверьте не упирается ли маятник в нижний кронштейн, между ними должен быть зазор не менее 1 см. 5. Включите установку в сеть переменного тока 220 В. Нажмите последовательно кнопки «Сеть» и «Сброс» на панели установки. Если установка исправна, на табло появятся нули. 6. Аккуратно намотайте нить на ось 10 так, чтобы диск с кольцом прижимался к щечкам электромагнита. Проверьте, удерживает ли электромагнит диск. 7. Нажмите кнопку «Пуск». Диск с кольцом начнет падать, и одновременно включится миллисекундомер. Когда диск прервет нижний световой луч отсчет времени прекратится. Запишите время падения t, отожмите кнопку «Пуск». Точность эксперимента существенно зависит от того, насколько аккуратно прижат диск к щечкам электромагнита: если сильно повернуть ось с диском, то нить растянется и силы упругости нити вместе с силами трения удержат диск в верхнем положении даже при отключенном электромагните. Повторите измерения не менее 10 раз и найдите среднее значение t. 8. Вычислите момент инерции I маятника с кольцом по формуле (35), измерив d штангенциркулем. 9. Рассчитайте момент инерции кольца по формуле I к = I - I о - I д. 10.Измерьте штангенциркулем внутренний R 1и внешний R 2 радиусы кольца. 11.Рассчитайте момент инерции кольца по формуле
Сравните этот результат со значением, полученным с помощью маятника Максвелла. 12.Проделайте эксперимент с двумя другими кольцами. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАБОТЕ 1. Опишите устройство маятника Максвелла. 2. Получите соотношения (35) и (39). 3. Как зависит период колебаний маятника Максвелла от его момента инерции? От длины нитей? 4. Диаметр оси маятника Максвелла, на которую наматывается нить, много меньше диаметра диска, который определяет момент инерции маятника. Почему бы в качестве маятника Максвелла не использовать однородный цилиндр? 5. Изобразите графически зависимости координат центра масс, линейной и угловой скорости, линейного и углового ускорения диска маятника Максвелла от времени. 6. *Какое влияние оказывает атмосферный воздух на период колебаний маятника Максвелла? РАЗДЕЛ N 3. МЕХАНИКА УПРУГИХ ТЕЛ Все реальные тела под воздействием сил в той или иной степени меняют свою форму, деформируются. Абсолютно упругое тело является самой простой моделью, в рамках которой учитывается возможность деформации (изменения формы) реальных тел.
Все разнообразие деформаций сводится к двум основным типам, которые можно назвать элементарными. Этими элементарными деформациями являются растяжение (и сжатие) и сдвиг. Наглядно представить эти деформации помогает рисунок 1. Здесь показано сечение параллелепипеда, жестко закрепленного на массивном жестком столе. Пусть внешняя сила равномерно распределена по верхней грани параллелепипеда. При этом, очевидно, такая же по величине, но обратная по направлению сила действует на параллелепипед со стороны стола. Существует два независимых направления силы по отношению к грани, к которой эта сила приложена: нормальное (на рисунке слева) и тангенциальное (на рисунке справа). В первом случае действие силы приводит к сжатию образца, если сила направлена внутрь тела, и к растяжению в противном случае. Количественной характеристикой растяжения (сжатия) является относительное удлинение
где l - длина параллелепипеда до приложения нагрузки, l' - во время действия внешней силы. При растяжении e>0, при сжатии e<0. Величину D l называют удлинением образца. Во втором случае (см. рисунок 1 справа) действие силы приводит к смещению слоев тела параллельно друг другу вдоль направления действия силы. Сдвиг характеризуется тангенсом угла g. При малых деформациях этот сдвиг мал и можно полагать tgg = g.
Исследование деформаций тел сводится к установлению зависимости e и g от приложенной нагрузки. В качестве меры последней выбирается величина f отношения приложенной внешней силы F к площади грани S, на которую эта сила непосредственно действует: f = F / S. Характерные результаты экспериментов по растяжению-сжатию образцов представлены на рисунке 2. Участок кривой АB соответствует так называемым упругим деформациям. Особенность их в том, что при снятии нагрузки меньшей fA (при растяжении) или fB (при сжатии) деформации исчезают. Если внешняя сила превысит предел упругости fA (fB) деформации станут неупругими. Т.е. при снятии нагрузки всегда будет иметь место некоторая остаточная деформация. Легко сообразить, что в области неупругих деформаций, нет однозначной зависимости между величиной приложенной нагрузки и величиной деформации. Такую ситуацию весьма затруднительно описать теоретически. Для упруго деформированного тела согласно закону Гука имеет место однозначная зависимость между приложенной нагрузкой и возникающей деформацией, которая в случае малых деформаций линейна: f n= E e, f t= G g1. (2) где E - модуль Юнга (модуль растяжения), G - модуль сдвига. Модель абсолютно упругого тела предполагает, что подобная линейная зависимость имеет место при любой деформации. Целью предлагаемых здесь упражнений является ознакомление с некоторыми экспериментальными методами определения упругих характеристик материалов - модуля Юнга и модуля сдвига. На практике для характеристики упругих свойств материалов наряду с модулем Юнга вместо модуля сдвига используют коэффициент Пуассона. Введение последнего основано на том факте, что любое сжатие или растяжение сопровождается изменением поперечных приложенной силе размеров образца (см. рис. 3). По определению коэффициент Пуассона
Знак минус в этом определении обусловлен тем обстоятельством, что сжатие (e<0) всегда сопровождается увеличением поперечных размеров тела (D a >0), а растяжение (e>0) - уменьшением (D a <0). Таким образом, коэффициент Пуассона положительная безразмерная величина. Так как энергия упругих деформаций положительная величина, можно показать, что m<1/2, (4) и имеет место связь
Таким образом,
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАЗДЕЛУ 1. Какие деформации являются элементарными? Как можно классифицировать деформации сгиба и кручения? 2. Ознакомьтесь с понятиями: упругие, неупругие, пластические, остаточные деформации, предел упругости, область текучести, предел прочности. 3. Что такое упругий гистерезис? 4. В чем состоит упрощение реальной ситуации, предлагаемое моделью абсолютно упругого тела? 5. Сформулируйте закон Гука. 6. Дайте определения модуля Юнга, коэффициента Пуассона, модуля сдвига. 7. Почему в качестве величин, характеризующих упругие свойства материалов выбирают пару: модуль Юнга - коэффициент Пуассона, а не пару: модуль Юнга - модуль сдвига? 8. *Получите соотношения (4) и (5). 9. *Рассчитайте работу, которую необходимо затратить на однородное растяжение (сжатие) стержня длиной l и площадью поперечного сечения S на величину D l для двух случаев: 1. внешняя сила в каждый момент времени чуть-чуть превосходит силу упругости; 2. внешняя сила все время равна силе упругости деформированного на D l стержня. Объясните разницу. 10.*Модуль Юнга можно определить (см. формулы (1) и (2)) как силу, приходящуюся на единицу площади сечения образца, перпендикулярного силе, которая вызывает удлинение образца вдвое. Какие дополнительные оговорки требуется внести в это определение с учетом ответа на предыдущий вопрос? ЛАБОРАТОРНАЯ РАБОТА N 31. ИЗУЧЕНИЕ УПРУГИХ ДЕФОРМАЦИЙ Цель работы - экспериментальная проверка закона Гука, измерение модуля Юнга и модуля сдвига.
Упражнение 1. Экспериментальная проверка закона Гука. Измерение модуля Юнга. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА Приборы и принадлежности: исследуемая струна, закрепленная вертикально, два измерительных микроскопа, микрометр, измерительная линейка, набор гирь. Принципиальная схема установки показана на рисунке 1. С помощью микроскопов 1 и 2 проводят измерение удлинения участка струны 3 между микроскопами. В качестве меток используются кусочки миллиметровой бумаги приклеенные к струне. Нагрузку можно менять, подвешивая к струне гири 4. ХОД РАБОТЫ 1. Изучите правила работы с измерительными микроскопами, представленные в начале вводного раздела. 2. Добейтесь четкого изображения меток струны на фоне измерительных шкал микроскопов. 3. Снимите все гири со струны. Отметьте положение меток на струне по шкалам микроскопов. 4. Измерьте микрометром толщину струны d. Считая ее поперечное сечение кругом, рассчитайте его площадь S = p d 2/4. 5. Измерьте линейкой расстояние l между метками на струне. 6. Нагрузите струну гирей и измерьте по шкалам микроскопов величины, на которые сдвинутся метки на струне. Относительное удлинение участка струны между микроскопами l можно найти по формуле e = (D l 2 - D l 1)/ l где D l 1 - изменение положения верхней метки, D l 2 - изменение положения нижней метки. 7. Найдите силу тяжести F = mg и определите коэффициент жесткости струны k = F/ D l = F /(D l 2 - D l 1). 8. Определите нагрузку на единицу площади поперечного сечения струны f = F / S, где m - масса гири, g - ускорение свободного падения. 9. Повторите пункты 5 и 6 несколько раз для каждой из возможных нагрузок, проводя измерения e как при загрузке так и при разгрузке струны. 10.Постройте график зависимости e(f). Выделите на графике линейный участок. 11.Определите модуль Юнга. Очевидно, (см. формулу (2)) что он будет равен тангенсу угла наклона линейного участка графика e(f) к оси ординат. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К УПРАЖНЕНИЮ 1. В чем принципиальное отличие коэффициента жесткости и модуля Юнга? 2. Опишите цель эксперимента и способ ее реализации на конкретной экспериментальной установке. 3. Влияют ли на результаты эксперимента длина, толщина, масса струны? 4. С какой целью в работе используются два микроскопа? 5. Какие данные вашего эксперимента свидетельствуют о выполнении закона Гука? 6. Мысленно продолжите эксперимент, увеличивая нагрузку на струну. Как при этом поведет себя график e(f)? Упражнение 2. Измерение модуля сдвига способом крутильных колебаний. Деформацию кручения можно классифицировать как неоднородный сдвиг. Поэтому имеется возможность определения модуля сдвига по периоду свободных колебаний крутильного маятника, в котором струна изготовлена из исследуемого материала. Найдем связь между периодом колебаний крутильного маятника T и модулем сдвига материала струны. В работе 23 было показано, что период колебания крутильного маятника можно выразить через модуль кручения D и момент инерции I следующим образом
Модуль кручения D, по определению, связан с вращающим моментом M и углом j, на который закручена струна соотношением M = D j. (8)
Установим эту связь на основе теории упругости. Разобьем струну на коаксиальные трубки с внутренним радиусом r и внешним радиусом r +D r. В такой трубе выделим параллелепипед шириной rd a (см. рисунок 2). Из рисунка видно, что деформация, которую испытывает такой параллелепипед при кручении стержня, будет сдвигом. Запишем закон Гука для него:
где через dM обозначен момент силы dF t, действующей на основание выделенного параллелепипеда, dS - площадь этого основания. Из треугольника ABA' имеем: tgg= AA' / AB. Если углы j и g малы: g = r j/ l. Подставив это выражение в формулу (9), получим:
Проинтегрировав это выражение по a от 0 до 2p и по r от 0 до R (радиус струны), получим:
Сопоставляя это выражение с формулой (8), найдем модуль кручения
С учетом соотношения (7) получим рабочую формулу:
Итак, для измерения модуля сдвига струны крутильного маятника, необходимо измерить длину l и радиус R струны, момент инерции I и период собственных колебаний T крутильного маятника. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА Приборы и принадлежности: исследуемая струна, закрепленная вертикально, груз с известным моментом инерции, секундомер, микрометр, измерительная линейка, весы. В работе используется та же установка, что и в работе 23. ХОД РАБОТЫ 1. Измерьте длину струны l линейкой, а ее радиус R - микрометром. 2. Момент инерции груза найдите по методу, описанному в работе 23. Если вы используете груз правильной геометрической формы, его момент инерции можно рассчитать по соответствующим формулам из таблицы 1 второго раздела, измерив необходимые геометрические параметры и определив массу взвешиванием. 3. Секундомером измерьте период свободных колебаний маятника. 4. По формуле (10) рассчитайте модуль сдвига. Оцените погрешность измерения. 5. Из формулы (5) выразите коэффициент Пуассона для материала струны и рассчитайте его, используя результаты этого и предыдущего упражнений. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К УПРАЖНЕНИЮ 1. В чем принципиальное отличие модуля кручения D и модуля сдвига G? 2. Опишите цель эксперимента и способ ее реализации на конкретной экспериментальной установке. 3. Воспроизведите самостоятельно вывод рабочей формулы (10). 4. Как влияют на точность эксперимента момент инерции маятника, длина и толщина струны? 5. Можно ли с помощью имеющихся в лаборатории приборов определить коэффициент Пуассона путем прямого измерения поперечных размеров струны? **Упражнение 3. Измерение модуля Юнга из изгиба Изгиб классифицируется как неоднородное растяжение-сжатие. Получим формулу, связывающую параметры изгиба и модуль Юнга. Рассмотрим изгиб бруса (балки) произвольного сечения, постоянного по всей длине балки. Пусть до деформации брус имел прямолинейную форму (рис. 3). Мысленно проведя нормальные к оси бруса сечения AB и A'B', вырежем бесконечно малый элемент бруса ABA'B', длину которого обозначим через l 0. Ввиду малости последней можно считать, что в результате изгиба отрезки AA', BB', NN' и все отрезки параллельные им перейдут в дуги окружности с центром на некоторой оси O,перпендикулярной плоскости рисунка (см. рис. 3). Эта ось называется осью изгиба. Наружные волокна, лежащие выше линии NN', при изгибе удлиняются, волокна, лежащие ниже линии NN', - укорачиваются. Длина отрезка NN' остается неизменной. Линия NN' называется нейтральной линией. Проходящее через нее сечение (недеформированного) бруса плоскостью, перпендикулярной плоскости рисунка, называется нейтральным сечением. Пусть R - радиус кривизны нейтрального сечения (R = | NO |). Тогда l 0=a R. Рассмотрим волокно бруса, находящееся на расстоянии x от нейтрального сечения. (x>0, если волокно выше нейтрального слоя, x<0, если - ниже.) Пусть брус не слишком толст, так что x<< R. Тогда длина рассматриваемого волокна равна l = a(R +x), а его удлинение D l = l - l 0 = xa. Такое удлинение сообщается нормальной к AB силой, величина которой в расчете на единицу площади сечения AB равна:
Будем считать, что мы имеем дело только с деформацией изгиба, т.е. сумма сжимающих и растягивающих сил, приложенных сечению AB равна нулю: Очевидно, или где введено обозначение
Величина I называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако в отличие от последней величины, имеющей размерность массы, умноженной на квадрат длины, I, определяемый выражением (14), имеет размерность четвертой степени длины. Для бруса с поперечным сечением в виде прямоугольника с шириной a и высотой (AB) b легко получить
Направим ось X вдоль нейтральной линии недеформированного бруса, ось Y - перпендикулярно X в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде y = y (x). По известной из математического анализа формуле
Если изгиб мал (y '<<1), то квадратом производной можно пренебречь. Тогда Ms = EIy". (16)
Рассмотрим теперь балку, лежащую на двух опорах (см. рис. 4). Расстояние между опорами равно L. Пусть на балку действует вертикальная сила F. Вследствие симметрии сила F равномерно распределится между опорами. Расстояние между точками О и О' (положениями центра масс до и после изгиба) называется стрелой прогиба. Обозначим ее через z. Поместим начало координат в точку A, направим ось X вправо, а Y - вниз. Отсечем мысленно часть балки, проведя нормальное сечение через произвольную точку С (x) (с координатой x < L /2). Справа на отсеченную часть балки будет действовать сила F /2, направленная вниз. Момент внешних сил, действующих на отсеченную часть, будет M = (F /2) x. Условие равновесия моментов принимает вид
Знак минус в правой части обусловлен выбором системы координат: функция y (x), описывающая положение нейтральной линии, замедленно растет при x < L /2. Интегрируя уравнение (17) с учетом того, что y '(L /2) = 0 и y (0) = 0, найдем
Тогда с учетом (15) получим стрелу прогиба для балки прямоугольного сечения
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА Приборы и принадлежности: измерительная линейка, индикатор малых перемещений (индикатор), штангенциркуль, набор гирь, исследуемые балки, опоры. Экспериментальная установка схематично изображена на рисунке 5. Прогиб балки 1, лежащей на опорах 2, создается весом гири 3. Стрела прогиба измеряется индикатором 4, укрепленным на подставке 5 с винтами 7. Вертикальное положение индикатора можно изменять винтом 6.
Из выражения (19) легко получить рабочую формулу:
где m - масса гири, g - ускорение свободного падения. ХОД РАБОТЫ 1. Установите опору 5 горизонтально (см. рис. 5), вращая винты 7. 2. Измерьте линейкой расстояние L между вершинами опор 2, а штангенциркулем толщину b и ширину a балки. 3. Положите балку на опоры. Вращая винт 6 (см. рис. 5), поднимите индикатор до касания с нижней поверхность балки. Поверните обод индикатора, чтобы положение стрелки совпало с нулем шкалы. Слегка постукивая по столу добейтесь устойчивого положения стрелки индикатора. 4. Положите гирю на балку. Слегка постукивая по столу добейтесь устойчивого положения стрелки индикатора, и определите по нему стрелу прогиба z. 5. Повторите измерения z несколько раз, меняя поворотом верхнюю и нижнюю стороны балки местами. Рассчитайте модуль Юнга по формуле (20). 6. Эксперимент повторите для всех имеющихся в распоряжении балок. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К УПРАЖНЕНИЮ 1. Изучите теорию изгиба, получите рабочую формулу. 2. **Проанализируйте, какой из двух методов измерения модуля Юнга, описанных в упражнениях 1 и 3, точнее теоретически? Сравните точности измерений модуля Юнга, полученные в ходе выполнения упражнений 1 и 2. Объясните результат сравнения. 3. Проведите сравнительный анализ измеренных модулей Юнга для разных материалов. 4. Если положить балку на опоры без гири, она все равно прогнется под действием собственного веса. Как это обстоятельство влияет на измерение стрелы прогиба и модуля Юнга? 5. В целях минимизации ошибки малые величины, входящие в знаменатели дробей, необход
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 894; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

 (29)
(29)
 (30)
(30)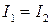 ), совершающий быстрое вращение вокруг оси симметрии (ось 3 на рис.7).
), совершающий быстрое вращение вокруг оси симметрии (ось 3 на рис.7). , (32)
, (32) , (33)
, (33) ,
, ;
; . (34)
. (34) Рис. 8.
Рис. 8.
 создайте вращающий момент
создайте вращающий момент  , где Р - вес противовеса (масса противовеса указана на нем).
, где Р - вес противовеса (масса противовеса указана на нем). , где j - угол поворота за время t. По индикатору 17 определите угловую скорость вращения диска гироскопа w. Подсчитайте значение величины wW. Следите за тем, чтобы ось гироскопа была горизонтальна.
, где j - угол поворота за время t. По индикатору 17 определите угловую скорость вращения диска гироскопа w. Подсчитайте значение величины wW. Следите за тем, чтобы ось гироскопа была горизонтальна. Рис. 9.
Рис. 9.
 . (35)
. (35) (37)
(37)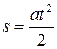 . (38)
. (38) . (39)
. (39) . (1)
. (1) . (3)
. (3)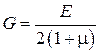 . (5)
. (5) . (6)
. (6)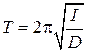 (7)
(7) (9)
(9) .
.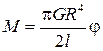 .
. .
. . (10)
. (10) . (11)
. (11) , где dS - элемент площади рассматриваемого поперечного сечения бруса, интегрирование ведется по всему этому сечению. С учетом выражения (11)
, где dS - элемент площади рассматриваемого поперечного сечения бруса, интегрирование ведется по всему этому сечению. С учетом выражения (11)  . Отсюда ясно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса (например, AB). Из
. Отсюда ясно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса (например, AB). Из  , (12)
, (12) , (13)
, (13) . (14)
. (14) . (15)
. (15) .
. . (17)
. (17) . (18)
. (18) . (19)
. (19) , (20)
, (20)


