
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ускорения свободного паденияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(ОБОРОТНЫЙ И СЕКУНДНЫЙ МАЯТНИКИ) Для определения ускорения g можно воспользоваться физическим маятником. Физическим маятником называется абсолютно твердое тело, которое может качаться вокруг неподвижной горизонтальной оси. При отсутствии силы трения уравнение движения маятника выглядит следующим образом:
где m - масса тела, I - момент инерции относительно точки подвеса, a - расстояние от точки подвеса до центра тяжести, j - угол отклонения маятника от положения равновесия. В случае малых колебаний в этом уравнении можно заменить sin j на j. В результате получим уравнение гармонического колебания с периодом:
Частным случаем физического маятника является математический маятник. Так называется гипотетический маятник, вся масса которого сосредоточена в одной точке. В этом случае формула (2) упрощается (так как I = ml2,a = l, где l- длина маятника) и для ускорения свободного падения получим:
Отсюда ясна идея одного из способов определения ускорения свободного падения. Необходимо измерить длину и период математического маятника. Сравнивая формулы (2) и (3), приходим к выводу, что физический маятник колеблется так же, как математический с длинной Важно иметь ввиду, что тот же самый период колебаний маятника может получиться при закреплении его, вообще говоря, в бесконечном множестве точек. Такие точки называются точками взаимности. Исходя из этого определения, центр качания и точка подвеса являются точками взаимности, но не единственно возможными. Поэтому расстояние между точками взаимности, которые легко установить по совпадению периодов колебаний, не всегда совпадает с приведенной длиной. Расстояние между точками взаимности равно приведенной длине физического маятника, только в том случае, если эти точки лежат на одной прямой с центром масс на разных расстояниях от него. Упражнение 1. Оборотный маятник
Оборотный маятник - устройство для определения ускорения свободного падения. Он состоит из стального стержня, на котором жестко закреплены опорные стальные призмы П 1 и П 2 и стальная чечевица А, находящаяся между ними (рис.1). Другая стальная чечевица В находится на одном из концов стержня (не между призмами), она может перемещаться по стержню и закрепляться в нужном положении. Перемещением этой чечевицы достигают совпадения периодов колебаний маятника, когда точками подвеса являются ребра опорных призм П 1 и П 2. В этом случае ребра призм будут точками взаимности. Эти ребра закреплены асимметрично относительно центра масс С. Поэтому при совпадении периодов колебаний расстояние между ними дает приведенную длину физического маятника l. Измерив период его колебаний T, можно вычислить g по формуле (3). ХОД РАБОТЫ 1. Линейкой измерьте расстояние l между призмами. 2. Подвесьте маятник на одну из призм. Отклоните маятник на небольшой угол. 3. Отсчитайте как можно больше полных колебаний и определите по секундомеру время t, за которое они совершаются, рассчитайте период колебания T 1. 4. Подвесьте маятник на другую призму и найдите период T 2. 5. Найдите периоды колебаний T 1 и T 2 для 7-10 положений чечевицы В. 6. На одном поле координат постройте графики зависимости периодов колебаний T 1 и T 2 от положения чечевицы. 7. Найдите точку пересечения графиков, определите период колебания в точке взаимности T = T 1 = T 2. 8. Рассчитайте g по формуле (3). Упражнение 2. Секундный маятник. Для измерения ускорения свободного падения можно использовать математический маятник, хорошим приближением к которому является массивный шарик на длинной по сравнению с его радиусом нити. Для точного измерения периода колебаний маятника используется способ биений (см. работу N 52). В качестве эталонной частоты выбирается частота колебаний секундного маятника, период которого составляет T c = 2с. ХОД РАБОТЫ 1. Наматывая нить математического маятника на кронштейн, добейтесь, чтобы длина маятника была немного меньше 1 метра. 2. Отклоните оба маятника в одну сторону и одновременно отпустите их. Сосчитайте количество колебаний n секундного маятника, через которое маятники опять будут двигаться синхронно. 3. Найдите период колебаний математического маятника по формуле 4. Вычислите g по формуле (3). 5. Увеличьте длину математического маятника до величины, немного превышающей 1 м. 6. Повторите пункты 2-4. 7. Найдите среднее значение g. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАБОТЕ 1. Что такое силы инерции? 2. Сформулируйте закон всемирного тяготения Ньютона. 3. Запишите уравнения движения материальной точки во вращающейся земной системе отсчета. Оцените величины входящих в него сил. 4. Что такое сила тяжести? Что такое ускорение свободного падения? 5. Оцените вклад в ускорение свободного падения центробежной силы Земли. 6. Что такое вес тела? 7. Какие проблемы возникают при определении массы тела путем взвешивания? 8. Докажите теорему Гюйгенса. 9. Опишите методы определения ускорения свободного падения, использованные в работе. Получите рабочие формулы. Какие допущения при этом используются и как они учтены в конструкции экспериментальных установок? 10.Получите формулу для периода колебаний, используемую в упражнении с секундным маятником. 11.Каковы преимущества использования секундного маятника по сравнению с секундомером? 12.В чем преимущества и недостатки методов измерения ускорения свободного падения с помощью оборотного и секундного маятников? РАЗДЕЛ N 5. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Колебаниями называются движения или процессы, обладающие той или иной периодичностью во времени. Это определение объединяет множество непохожих на первый взгляд процессов: колебания различных маятников, смену времен года, колебания численности популяций животных, колебательные химические реакции и т.д. Природа колебаний обусловлена свойствами систем (физическими, химическими, биологическими и т.д.) и условиями, в которых они находятся. Характеристики колебаний связаны с параметрами, определяющими состояние систем, а значит, исследуя колебания, можно делать выводы о строении и свойствах самых различных систем. Именно на этой идее основано множество мощных методов исследования веществ: акустическая спектроскопия, оптическая спектроскопия, открытый в Казанском университете электронный парамагнитный резонанс (ЭПР), ядерный магнитный резонанс (ЯМР) и др. Эти методы на основе анализа свойств регистрируемых колебаний позволяют изучать исследуемые системы. Например, с помощью метода ЯМР можно установить строение молекул и сделать определенные выводы об их окружении. На этом основан самый информативный и относительно безопасный метод медицинской диагностики - ЯМР-томография. Несмотря на огромное разнообразие колебательных процессов в природе и технике для их описания существует единый подход. Предлагаемые в данном разделе лабораторные работы дают возможность ознакомиться с ним на основе экспериментального исследования различных колебательных процессов в механических системах. Любая функция f, описывающая периодический процесс, должна удовлетворять соотношению Итак, гармоническим называется колебание происходящее по закону синуса или косинуса, т.е.
где, по определению, x 0 - амплитуда, (w0 t +j) - фаза, w0 - циклическая частота, j - начальная фаза колебаний. При этом циклическая частота w0 связана с частотой n0 и периодом T 0колебаний следующими соотношениями:
Легко убедиться непосредственной подстановкой, что функция (1) удовлетворяет уравнению
где точкой сверху обозначается производная по времени. Уравнение (3) называют уравнением гармонического осциллятора, а гармоническим осциллятором - модель колебательной системы, описываемую уравнением (3). Гармонический осциллятор характеризуется единственным параметром - циклической частотой колебаний w0. Модель осциллятора с затуханием, описываемая уравнением:
является более хорошим приближением к действительности. Уравнению (4) (убедитесь непосредственной подстановкой) при b < w0 удовлетворяют функции вида:
где Для наглядности на рис. 1 показаны графики функций (1) и (5). Модель осциллятора с затуханием учитывает, что после начального возмущения система стремится восстановить равновесное состояние, в котором колебания отсутствуют. Осциллятор с затуханием характеризуется двумя параметрами: b, определяющим уменьшение со временем амплитуды колебаний, и w0 - частотой колебаний в отсутствие затухания.
Из сказанного следуют цели предлагаемых работ по исследованию механических колебаний: Убедиться, что модель осциллятора с затуханием применима к ряду механических систем; Выяснить какие характеристики систем определяют частоту собственных колебаний и коэффициент затухания; Освоить методы измерения параметров осциллятора с затуханием. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАЗДЕЛУ 1. Что называется колебаниями? Какими параметрами характеризуются гармонические колебания? 2. Расскажите о кинематике колебаний. Обратите внимание на связи координаты со скоростью и ускорением. 3. Расскажите о моделях гармонического осциллятора и осциллятора с затуханием. 4. Покажите, что при некоторых условиях массивное тело, подвешенное на нити, удовлетворяет уравнению гармонического осциллятора (математический маятник). Чем в данном случае определяется частота собственных колебаний, и коэффициент затухания? 5. Маятник Фуко, с помощью которого было доказано суточное вращение Земли, представлял собой металлический шар массой 28 кг, подвешенный на проволоке длиной 67 м. Объясните подобный выбор параметров. 6. Покажите, что при некоторых условиях массивное тело, подвешенное на пружине, удовлетворяет уравнению гармонического осциллятора (пружинный маятник). Чем в данном случае определяется частота собственных колебаний и коэффициент затухания? Какое влияние на них оказывает сила тяжести? 7. * Рассмотрите способ описания колебаний с помощью комплексных чисел. ЛАБОРАТОРНАЯ РАБОТА N 51.
|
||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 933; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.237 (0.011 с.) |

 , (1)
, (1)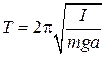 (2)
(2)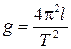 (3)
(3) . Эта величина называется приведенной длинной физического маятника. Точка, удаленная от точки подвеса на расстояние l вдоль прямой, проходящей через центр масс, называется центром качания. Если маятник подвесить за центр качания, то период его колебаний не изменится (теорема Гюйгенса).
. Эта величина называется приведенной длинной физического маятника. Точка, удаленная от точки подвеса на расстояние l вдоль прямой, проходящей через центр масс, называется центром качания. Если маятник подвесить за центр качания, то период его колебаний не изменится (теорема Гюйгенса).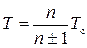 .
. (где t - время, а T - период функции f). В математике существует фундаментальная теоремаФурье, согласно которой любая периодическая[1] функция может быть представлена как сумма, вообще говоря, бесконечно большого числа гармонических (т.е. происходящих по закону синуса или косинуса) колебаний. Благодаря этой теореме, изучение сколь угодно сложных колебаний сводится к исследованию закономерностей гармонических колебаний[2].
(где t - время, а T - период функции f). В математике существует фундаментальная теоремаФурье, согласно которой любая периодическая[1] функция может быть представлена как сумма, вообще говоря, бесконечно большого числа гармонических (т.е. происходящих по закону синуса или косинуса) колебаний. Благодаря этой теореме, изучение сколь угодно сложных колебаний сводится к исследованию закономерностей гармонических колебаний[2].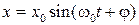 , (1)
, (1)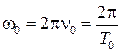 . (2)
. (2)
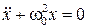 , (3)
, (3)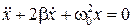 (4)
(4)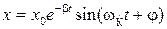 , (5)
, (5) - циклическая частота затухающих колебаний, b - коэффициент затухания, w0 - циклическая частота собственных (т.е. незатухающих) колебаний. Это уравнение описывает не периодический процесс, но при b<<w0 можно считать, что это уравнение описывает гармоническое колебание с изменяющейся амплитудой
- циклическая частота затухающих колебаний, b - коэффициент затухания, w0 - циклическая частота собственных (т.е. незатухающих) колебаний. Это уравнение описывает не периодический процесс, но при b<<w0 можно считать, что это уравнение описывает гармоническое колебание с изменяющейся амплитудой  .
.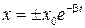 (пунктирная линия).
(пунктирная линия).
 и
и 


