
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка законов свободного падения телСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: проверка законов свободного падения тел на примере падения в воздухе шариков разной массы, определение ускорения свободного падения и массы Земли.
Приборы и принадлежности: рейка с платформами и измерительной линейкой, электромагнит, секундомер, одинаковые шарики различной массы. Схема экспериментальной установки:
Методика исследования и описание установки Экспериментальные исследования показали, что свободное падение - равноускоренное движение и ускорение свободного падения g - зависит от географической широты и расстояния от центра Земли, но не зависит от массы тела, т.е. все тела в одном и том же месте Земли падают с одним и тем же ускорением. Независимость ускорения свободного падения от массы приводит к выводу, что отношение гравитационной массы m g, которая входит в закон всемирного тяготения, к массе инертной mин, которая входит во второй закон Ньютона, есть величина постоянная. К такому результату приводят все опыты, в которых могло бы проявиться различие между инертной и гравитационной массами. А это означает, что при надлежащем выборе единиц измерения m g и mин становятся тождественными, поэтому в физике говорят просто о массе m. Всё изложенное выше можно обосновать теоретически, рассматривая движение относительно той или другой системы отсчета. Так, например, если свободное падение рассматривать относительно инерциальной системы отсчета (движущейся без ускорения), связанной с Землей, то оно происходит под действием силы тяготения:
где m g – гравитационная масса тела; М - гравитационная масса Земли; G - гравитационная постоянная. Эта сила вызывает ускорение:
или если центр тяжести тела поднять на высоту h, то
Зависимость g от h будет ощутимой при соизмеримости h и R. Зависимость g от географической широты легко показать, если свободное падение рассматривать относительно неинерциальной системы отсчета, связанной с Землей, т.е. с учетом суточного вращения Земли с угловой скоростью ω. В этом случае (рис.2) на тело массой m, находящееся на широте φ, действуют две силы: сила тяготения (1) и сила инерции:
Сила инерции зависит от географической широты. Сила тяжести
Угол отклонения
Установка для изучения свободного падения тел состоит из вертикальной штанги с линейкой (рис. 1). По штанге перемещаются две платформы. К верхней прикреплён электромагнит, удерживающий металлический шарик, а к нижней ловушка с контактной заслонкой. Запуск секундомера производится в момент отрыва шарика от электромагнита, а его остановка в момент достижения шариком ловушки. Изменяя положение ловушки, мы меняем h, а значит, и время падения. По значениям h и t строится график зависимости Ускорение свободного падения определяется из уравнения равноускоренного движения
Порядок проведение работы
1. По указанию преподавателя откройте программу, содержащую блок лабораторных работ по физике, раздел «механика, статистическая физика и термодинамика». Выберите нужную вам лабораторную работу. 2. Еще раз внимательно прочитайте теорию и методику проведения работы. Для этого щелкните левой клавишей на экране кнопку. «Теория и методика проведения работы». 3. Откройте flash-анимацию. 4. По указанию преподавателя с помощью мыши задайте высоту падения шарика и его массу. 5. Щелкните кнопку «Старт» для начала эксперимента. 6. Занесите полученное значение времени в таблицу 1. 7. Щелкните кнопку «Сброс» и, не меняя высоту падения шарика и его массу, повторите опыт 10 раз. 8. Не меняя высоты падения шарика, проделайте пункты 4-7. 9. Щелкните кнопку «Перейти к заданию 2». 10. По указанию преподавателя, изменяя высоту падения шарика, замерьте время падения с десяти разных высот, каждый раз занося данные в таблицу 2. 11. При помощи калькулятора произведите вычисления предлагаемых величин. 12. Сделайте вывод о проделанной работе. 13. Ответьте на контрольные вопросы.
Обработка результатов измерений 1. По результатам, полученным при выполнении первого задания, сделайте вывод. 2. По результатам, полученным при выполнении второго задания, по формуле (6) рассчитать ускорение свободного падения для каждого опыта. 3. Погрешности для g рассчитать как при многократных измерениях. 4. Массу земли рассчитать по формуле где 5. Погрешности для массы Земли определить как при многократных измерениях. 6. Постройте график зависимости Таблица измерений № 1
Таблица измерений № 2
Контрольные вопросы: 1) Что называется силой тяжести? 2) Какое движение называется свободным падением? 3) Почему ускорение свободного падения не одинаково в различных точках земной поверхности? 4) Дайте определение инерциальной и неинерциальной систем отсчета. 5) Какие силы действуют на земные тела, если систему отсчета связанную с Землей считать инерциальной и неинерциальной? Лабораторная работа №5
Определение коэффициента вязкости жидкости
Цель работы: определить коэффициент вязкости жидкости. Приборы и принадлежности: сосуд с жидкостью, секундомер, масштабная линейка, штангенциркуль, шарики. Схема экспериментальной установки:
Методика исследования и описание установки При движении жидкости между ее слоями возникают силы внутреннего трения противостоящие «сдвигу» слоев, действующие таким образом, чтобы уровнять скорости всех слоев. Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному слою некоторый импульс, что приводит к торможению последнего. Сила внутреннего трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения ∆S и градиенту скорости
Величина η называется коэффициентом внутреннего трения или вязкости. Коэффициент вязкости зависит от природы жидкости и для данной жидкости с повышением температуры вязкость уменьшается. При падении шарика в вязкой жидкости на него действуют три силы: 1. Сила тяжести 2. Выталкивающая сила Архимеда 3. Сила внутреннего трения, действующая на шарик радиуса r при его медленном поступательном движении со скоростью u и тормозящая движение шарика, которая определяется по формуле Стокса На основании второго закона Ньютона имеем:
Вначале скорость движения шарика возрастает
С этого момента движение шарика становится практически равномерным со скоростью
Скорость равномерного движения шарика Учитывая, что на опыте измеряется диаметр шарика, а не его радиус получаем расчетную формулу:
Порядок выполнения работы 1. По указанию преподавателя откройте программу, содержащую блок лабораторных работ по физике, раздел «механика, статистическая физика и термодинамика». Выберите нужную вам лабораторную работу. 2. Еще раз внимательно прочитайте теорию и методику проведения работы. Для этого щелкните левой клавишей на экране кнопку. «Теория и методика проведения работы». 3. Откройте flash - анимацию, для этого щелкните кнопку «Эксперимент». 4. Задайте параметры – вид жидкости, диаметр шарика, величину MN. 5. Щелкните кнопку «Пуск» для начала эксперимента. 6. Запишите параметры установки и время падения шарика в таблицу. 7. Повторите опыт 10 раз, изменяя параметры. 8. При помощи калькулятора произведите вычисления предлагаемых величин. 9. Сделайте вывод о проделанной работе. 10. Ответьте на контрольные вопросы.
Обработка результатов измерений
1. Коэффициент вязкости рассчитывается по формуле (5). 2. Относительную погрешность каждого опыта рассчитать по формуле
3. Абсолютную погрешность каждого опыта рассчитать по формуле
Таблица измерений
Контрольные вопросы: 1) Сформулируйте закон Архимеда. 2) Вследствие чего возникают силы внутреннего трения? Как они направлены? 3) Является ли сила сопротивления среды силой внутреннего трения? Обоснуйте ответ. 4) Напишите формулу Стокса. Дайте определения величин, входящих в формулу. 5) Какие силы действуют на шарик, падающий в жидкости? 6) На каком участке траектории падающего шарика результирующая сила изменяет своё значение с ростом скорости? 7) На каком участке траектории падающего шарика результирующая сила равна нулю? Каков характер движения шарика на этом участке? 8) Выведите единицу измерения h, используя расчётную формулу.
Лабораторная работа №6
Определение отношения молярных теплоемкостей газа СР ¤ СV методом адиабатического расширения
Цель работы: изучить термодинамические процессы в воздухе и определить отношение теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме методом адиабатического расширения (методом Клемана-Дезорма). Приборы и принадлежности: прибор Клемана-Дезорма. Теоретические сведения Теплоемкостью какого-либо вещества, называется физическая величина, численно равная количеству теплоты dQ, которое нужно сообщить телу, чтобы повысить его температуру на один градус: Теплоемкость единицы массы вещества называется удельной теплоемкостью, С Молярной теплоемкостьюназывается физическая величина, численно равная теплоте, которую нужно сообщить одному молю вещества при изменении его температуры на один кельвин в рассматриваемом термодинамическом процессе, С
Величина теплоемкости зависит от условий, при которых происходит нагревание вещества. Рассмотрим ……. В соответствии с первым началом термодинамики сообщение газу количества теплоты
· При изохорном нагревании объем газа V остается постоянным, где · При изобарном нагревании газа давление остается постоянным. Газ, расширяясь, совершает работу (для одного моля газа) Следовательно, Таким образом, теплоемкость при постоянном давлении
Отношение молярных теплоемкостей, является одной из важных термодинамических величин и называется показателем адиабаты (коэффициентом Пуассона)
Величина показателя адиабаты зависит только от числа степеней свободы газовых молекул: для одноатомных газов
для двухатомных газов (молекулы с жесткими связями)
для многоатомных газов (молекулы с жесткими связями)
В данной работе показатель адиабаты определяется для воздуха, который в основном состоит из двухатомных молекул О2, N2, … и с определенной погрешностью может быть описан с помощью уравнений используемых для идеального газа. В эксперименте реализуется адиабатно-изохорно-изотермический цикл. Циклом или круговым процессом называется совокупность термодинамических процессов, в результате которых система возвращается в первоначальное состояние. Адиабатическим называется термодинамический процесс, протекающий без теплообмена с окружающей средой. Уравнением адиабатического процесса является уравнение Пуассона:
Изохорным называется термодинамический процесс, протекающий при постоянном объеме (V =const), то есть
Изотермическим называется термодинамический процесс, протекающий при постоянной температуре (T=const), то есть
Описание установки и методика проведения эксперимента
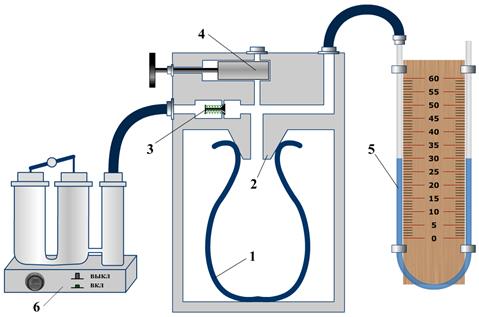
1. баллон 2. насадка 3. клапан 4. кран К 5. манометр 6. насос
Рис.1
Прибор Клемана - Дезорма состоит из баллона с воздухом 1, водяного манометра 5 и насоса 6. Баллон с воздухом 1, через насадку 2 может сообщаться либо с насосом через клапан 3, либо с атмосферой через кран 4. В настоящей работе реализуется классический метод, основанный на исследовании поведения некоторой массы газа, последовательно проходящего через три состояния (см. диаграмму рV, рис.2). Из состояния 1 в состояние 2 газ переходит путем адиабатического расширения, из 2 в 3 – изохорически, из 3 в 1 – изотермически. В исходном состоянии кран 4 открыт и давление в баллоне равно атмосферному давлению р2 = р атм. Закроем кран и с помощью насоса быстро накачаем воздух в баллон. При сжатии повышается давление воздуха относительно атмосферного, при этом воздух нагревается. Давление, установившееся в баллоне
где р 2 – атмосферное давление, измеренное в мм вод. столба,
Работа, затраченная на сжатие газа, превращается в теплоту, которая отводится через стенки баллона в атмосферу. То есть вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха в баллоне сравнится с температурой внешней среды Т 1 (изохорное охлаждение). Таким образом, состояние воздуха внутри баллона (состояние 1 на рис.2) характеризуется параметрами р1,V1,Т1.
Рис.2
Пусть масса воздуха после накачивания насосом в баллон объемом V 2 равна m. Откроем кран, при этом часть воздуха выходит из баллона. Обозначим массу вышедшего воздуха Δm, тогда масса оставшегося воздуха Состояние воздуха в баллоне после расширения до закрытия крана (состояние 2) характеризуется параметрами p 2, V 2, T 2. Для газа массой m1 1 и 2 состояния связаны уравнением Пуассона:
При повторном закрывании крана и отключении баллона от атмосферы воздух изохорно нагревается вследствие теплообмена с окружающей средой, температура и давление увеличиваются при постоянном объеме, столбики манометра расходятся до расстояния Состояния 1 и 3 связаны уравнением Бойля – Мариотта (так как T =const)
Откуда
Для дальнейших преобразований разложим
Подставляя эти выражения в формулу (8), получим
Итак, для определения показателя адиабаты γ необходимо измерить разность уровней жидкости в коленах манометра перед адиабатическим расширением и после него. Порядок выполнения работы
1. Накачать воздух в баллон так, чтобы величина ∆h 1, показываемая U-образным манометром составляла 20-25 см вод.ст.. Значение ∆h 1 записать в таблицу. 2. Открыть кран, при этом давление и температура газа понижаются, и столбики жидкости в коленах манометра уравниваются. 3. Закрыть кран, отключив баллон с газом от атмосферы. Дождаться нагревания воздуха в баллоне. Зарегистрировать перепад давления ∆h 2. Записать полученное значение в таблицу. 4. Повторить опыт 10 раз. 5. При помощи калькулятора произвести вычисления. 6. Сделать вывод о проделанной работе. 7. Ответить на контрольные вопросы.
Обработка результатов измерений 1. Показатель адиабаты γ рассчитать по формуле (9). 2. Относительную погрешность определить как при многократных измерениях по формуле
Таблица измерений
Контрольные вопросы: 1) Дать определение молярной и удельной теплоемкости. 2) Объяснить, почему теплоемкость газа зависит от условий теплообмена. 3) Что понимают под числом степеней свободы. Сформулируйте закон равномерного распределения энергии. 4) Какова связь между молярными теплоемкостями С P и С V и числом степеней свободы? 5) Сформулируйте первое начало термодинамики. 6) Какой процесс называется адиабатическим, и какому уравнению состояния этот процесс подчиняется? Нарисовать график процесса в координатах рV, VТ, ТS. 7) В каких пределах может изменяться показатель адиабаты для идеальных газов? Лабораторная работа №7 ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС
Цель работы: экспериментальная проверка закона Бойля-Мариотта, определение работы изотермического сжатия (расширения) газа. Приборы и принадлежности: лабораторная установка «Изотерма». Теоретические сведения Температура - мера интенсивности теплового движения частиц, образующих систему, или степень нагретости тела. Для измерения температуры пользуются температурными шкалами. Абсолютную шкалу температуры называют так же шкалой Кельвина. Эта шкала принята за основную шкалу в Международной системе единиц измерения (СИ). Один градус по этой шкале принят за единицу температуры и обозначается буквой Как в шкале Кельвина, так и в шкале Цельсия разность температур замерзания и кипения воды равна 100 градусам, поэтому на этих шкалах масштаб одного градуса одинаков. Один градус по шкале Фаренгейта, до сих пор используемой в США, равен 5/9 градуса по Цельсию. Полагают, что при температуре равной 0 К всякое движение молекул прекращается. Такую температуру называют абсолютным нулем, она соответствует Изотермическим называетсяпроцесс, происходящий в термодинамической системе при постоянной температуре Изотермический процесс осуществляется при условии постоянства температуры тел, окружающих газ, и настолько медленного изменения объема газа и давления, что температура газа в любой момент не отличается от температуры окружающих тел. Закон Бойля-Марриота: при неизменной температуре и массе произведение численных значений давления и объема газа постоянно
Термодинамические диаграммы изотермического процесса.
Изотермический процесс может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной разности температур. Для этого процесс расширения (сжатия) должен происходить очень медленно. Равновесным состоянием системы называется такое состояние, при котором все параметры системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго. Реальный процесс изменения состояния системы будет тем ближе к равновесному процессу, чем медленнее он совершается, поэтому равновесные процессы часто называют квазистатическими. Энергия, передаваемая термодинамической системе внешними телами при силовом взаимодействии, называется работой, совершаемой над системой. Элементарная работа газа в равновесном квазистатическом процессе изменения его объема определяется выражением:
При подводе теплоты происходит расширение газа и увеличение объема, сопровождающееся уменьшением давления. При отводе теплоты происходит сжатие газа и уменьшение объема, сопровождающееся увеличением давления. Так как
Поэтому, в соответствии с первым началом термодинамики, вся теплота, сообщаемая газу в ходе процесса, расходуется на совершение газом работы против внешних сил, т.е.
Работа изотермического расширения (сжатия) газа может быть рассчитана по формуле:
Преобразуем выражение (5), используя уравнение Менделеева-Клапейрона
откуда Таким образом,
Описание установки и методика проведения эксперимента
1- сосуд с газом; 2- поршень; 3- датчик изменения объема; 4- винт; 5- датчик давления; 6- вакуумный шланг.
Установка представляет собой герметичный сосуд 1 (полупрозрачный цилиндр из пластика), составляющий единую конструкцию с датчиком изменения объема 3. Объем сосуда изменяется от 30 до 110 мл при движении внутри его поршня 2, осуществляемого за счет вращения винта 4. Калибровка датчика объема учитывает объем шланга, поэтому показания датчика на 10 мл больше величины объема газа в сосуде, измеренной по шкале на стенке сосуда. С поршнем жестко связана подвижная часть датчика изменения объема. Давление газа измеряется датчиком абсолютного давления 5, который присоединен к цилиндру с помощью вакуумного шланга 6. Стенки сосуда обладают достаточной теплопроводностью, чтобы обеспечить равенство температуры газа температуре окружающей среды при условии медленного изменения объема и давления (при вращении подающего поршень винта). Быстрое перемещение поршня может привести к несоблюдению условия изотермичности процесса. Определим массу газа в сосуде из начальных условий. Воспользуемся уравнением состояния идеального газа (уравнением Менделеева-Клапейрона):
Откуда
где р1,V1,Т1 – начальные значения давления, объема и термодинамической температуры, m – масса газа, μ - молярная масса газа (для воздуха μ= 0,029 кг/моль), R= 8,31 Дж/(моль·К) - универсальная газовая постоянная. Температуру Т і газа в сосуде (в ходе процесса) можно рассчитать по формуле
где рі, – текущие значения давления.
Порядок выполнения работы
1.Задать начальную температуру (выбрать из списка), в соответствии с температурой окружающей среды в аудитории. 2. Выбрать крайнее нижнее или крайнее верхнее положение (по указанию преподавателя). Включить датчики, нажав на кнопку «включить датчики». 3. Медленно вращая рукоятку винта, перевести поршень в другое крайнее положение. В процессе перемещения поршня будут изменяться параметры газа. В правой части экрана начнет строиться график р=р(V). 4. Выбрать на графике несколько точек (10-15). Для этого навести указатель мышки на одну из точек графика, и щелкнуть левой клавишей. На экране появятся численные значения объема и давления. Занести данные в таблицу. 5. При помощи калькулятора произвести вычисления. 6. Сделать вывод о проделанной работе. 7. Ответить на контрольные вопросы.
Обработка результатов измерений 1. Рассчитать массу газа в сосуде по формуле (9), используя начальные значения р1,V1,Т1. 2. По формуле (10) рассчитать температуру газа для различных значений рі и Vі. Сравнить ее среднее значение с температурой окружающей среды. 3. По формуле (8) рассчитать работу А расширения (сжатия) газа.
Таблица измерений
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.194.29 (0.012 с.) |


 , (1)
, (1) (2)
(2) . (3)
. (3) . (4)
. (4) является равнодействующей этих двух сил, т.е.
является равнодействующей этих двух сил, т.е.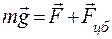 . (5)
. (5) 
 самый большой на широте φ = 450 и равен 6'. Таким образом, сила тяжести совпадает по направлению с
самый большой на широте φ = 450 и равен 6'. Таким образом, сила тяжести совпадает по направлению с  , то и в этом случае можно считать, что
, то и в этом случае можно считать, что  и прийти к формулам (3), (4), но, учитывая сплюснутость Земли, считать радиус Земли зависящим от географической широты. В данной работе используется высота h << R, и поэтому зависимость g от h не учитывается.
и прийти к формулам (3), (4), но, учитывая сплюснутость Земли, считать радиус Земли зависящим от географической широты. В данной работе используется высота h << R, и поэтому зависимость g от h не учитывается. , который даёт возможность судить о том, что свободное падение – равноускоренное движение.
, который даёт возможность судить о том, что свободное падение – равноускоренное движение. , откуда
, откуда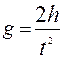 . (6)
. (6) , (7)
, (7) м3/кг∙с2,
м3/кг∙с2,  м.
м.
 в направлении внешней нормали n к поверхности слоя:
в направлении внешней нормали n к поверхности слоя: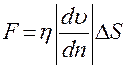 . (1)
. (1) (V - объем и ρ - плотность шарика)
(V - объем и ρ - плотность шарика) (ρ ’ – плотность жидкости)
(ρ ’ – плотность жидкости) .
.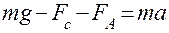 или
или  (2)
(2) , но так как по мере увеличения скорости сила сопротивления так же возрастает, то наступает такой момент, когда сила тяжести уравновешивается суммой сил Архимеда и Стокса и равнодействующая всех сил становится равной нулю.
, но так как по мере увеличения скорости сила сопротивления так же возрастает, то наступает такой момент, когда сила тяжести уравновешивается суммой сил Архимеда и Стокса и равнодействующая всех сил становится равной нулю. . (3)
. (3) . Решая уравнение движения относительно
. Решая уравнение движения относительно  , получим для коэффициента вязкости:
, получим для коэффициента вязкости: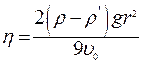 . (4)
. (4)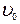 можно определить, зная расстояние ℓ между метками на сосуде и время t, за которое шарик проходит это расстояние
можно определить, зная расстояние ℓ между метками на сосуде и время t, за которое шарик проходит это расстояние  .
. . (5)
. (5) .
.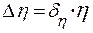 .
. .
.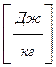 .
. .
. расходуется на увеличение внутренней энергии газа
расходуется на увеличение внутренней энергии газа 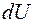 и совершением газом работы
и совершением газом работы 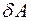 :
: .
. , и газ не совершает работу
, и газ не совершает работу  ; тогда
; тогда  и молярная теплоемкость при постоянном объеме определяется так:
и молярная теплоемкость при постоянном объеме определяется так:  ,
, - внутренняя энергия одного моля идеального газа, і - число степеней свободы молекулы газа.
- внутренняя энергия одного моля идеального газа, і - число степеней свободы молекулы газа.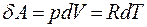 .
.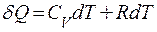 .
. .
. :
: .
. :
: ,
, :
: ,
, :
: .
. .
. .
. .
. Рассматриваемый метод определения СР ¤ СV и экспериментальная установка для его реализации впервые были предложены французским ученым Клеман-Дезормом в 1819 году. Схема экспериментальной установки представлена на рис. 1.
Рассматриваемый метод определения СР ¤ СV и экспериментальная установка для его реализации впервые были предложены французским ученым Клеман-Дезормом в 1819 году. Схема экспериментальной установки представлена на рис. 1. ,
, - показание манометра (разность уровней жидкости в коленах манометра), выраженное в тех же единицах измерения, что и р2.
- показание манометра (разность уровней жидкости в коленах манометра), выраженное в тех же единицах измерения, что и р2.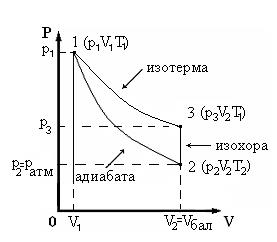
 . Эта масса перед открытием крана занимала меньший объем V 1 (V 1 – часть объема V 2) при давлении р1 и температуре Т1 . Так как процесс выпускания воздуха кратковременный и заметного теплообмена между газом и стенками баллона нет, то его можно считать процессом адиабатического расширения. Адиабатическое расширение сопровождается понижением давления в нашем случае до атмосферного p2 (столбы водяного манометра уравниваются) и понижением температуры до
. Эта масса перед открытием крана занимала меньший объем V 1 (V 1 – часть объема V 2) при давлении р1 и температуре Т1 . Так как процесс выпускания воздуха кратковременный и заметного теплообмена между газом и стенками баллона нет, то его можно считать процессом адиабатического расширения. Адиабатическое расширение сопровождается понижением давления в нашем случае до атмосферного p2 (столбы водяного манометра уравниваются) и понижением температуры до 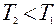 .
. или
или  . (3)
. (3) (состояние 3). Состояние 3 характеризуется параметрами
(состояние 3). Состояние 3 характеризуется параметрами  , V 2, T 1.
, V 2, T 1. или
или  . (4) Возведем уравнение (4) в степень γ:
. (4) Возведем уравнение (4) в степень γ:  . (5) На основании (3) и (5) запишем:
. (5) На основании (3) и (5) запишем:  . (6) Логарифмируя соотношение (6), получим:
. (6) Логарифмируя соотношение (6), получим: . (7)
. (7) . (8)
. (8) и
и 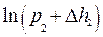 в ряд Тейлора, ограничившись двумя первыми членами:
в ряд Тейлора, ограничившись двумя первыми членами: .
. . (9)
. (9) .
. , %
, %
 (называется кельвином), например, температура замерзания воды или плавления льда должна записывается как
(называется кельвином), например, температура замерзания воды или плавления льда должна записывается как  . По шкале Цельсия, которая широко используется во всех странах (в США она не признана официально), температура замерзания воды принята за ноль (обозначается как
. По шкале Цельсия, которая широко используется во всех странах (в США она не признана официально), температура замерзания воды принята за ноль (обозначается как  ).
). .
. .
. . (1)
. (1)
 . (2)
. (2)
 , то внутренняя энергия идеального газа в изотермическом процессе не изменяется, то есть
, то внутренняя энергия идеального газа в изотермическом процессе не изменяется, то есть . (3)
. (3) . (4)
. (4) . (5)
. (5) , (6)
, (6) . (7)
. (7)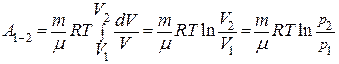 . (8)
. (8)
 ,
, . (9)
. (9) , (10)
, (10)


